3-Digit Subtraction with Regrouping - Definition, Examples, Quiz, FAQ, Trivia
Learn to subtract large numbers using regrouping with step-by-step methods and practice activities
What is Subtraction with Regrouping?
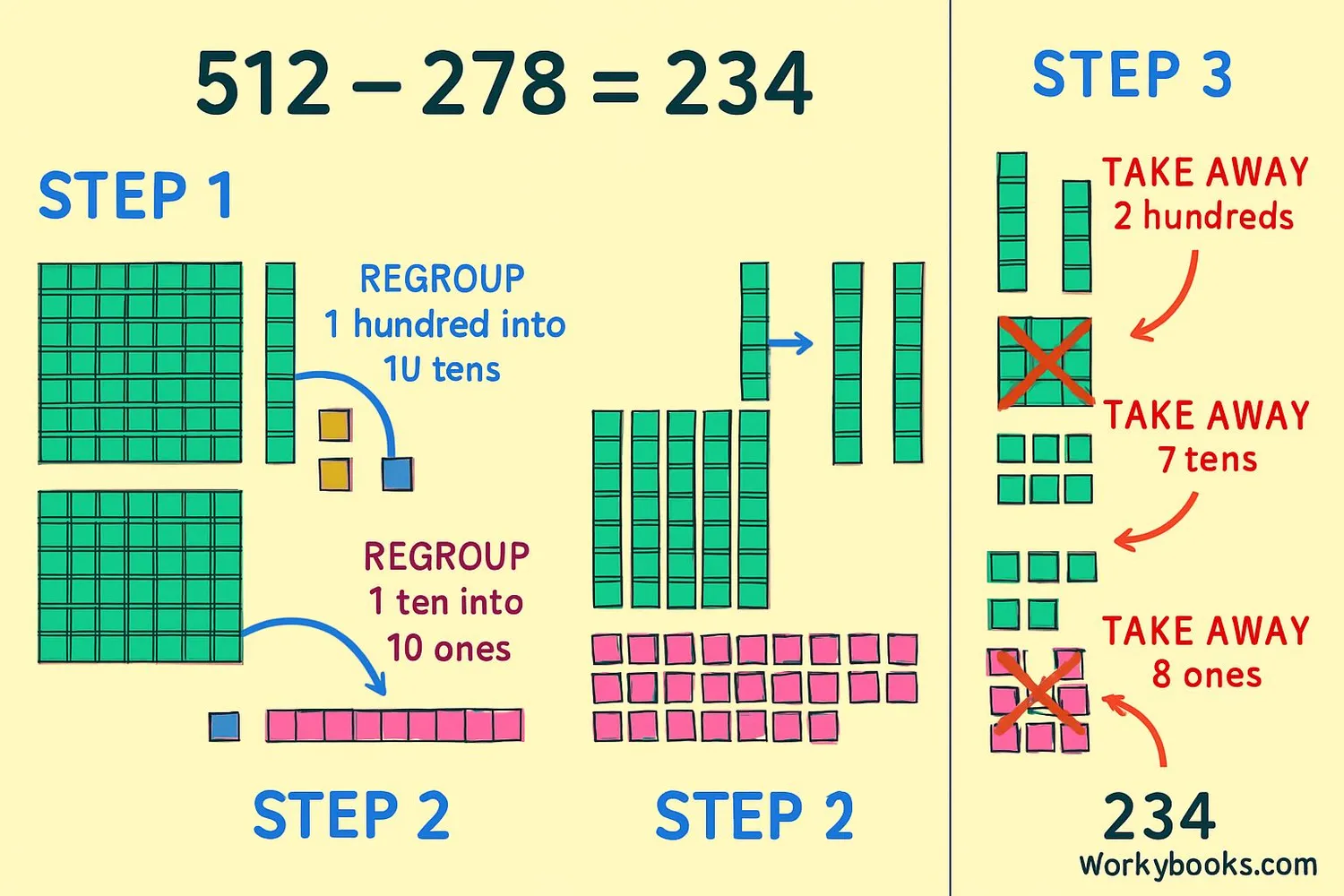
Subtraction with regrouping (also called borrowing) is a method we use when a digit in the minuend (top number) is smaller than the digit in the subtrahend (bottom number) in the same place value. We "borrow" from the next higher place value to make the subtraction possible.
Key Terms:
• Minuend: The number we're subtracting from (top number)
• Subtrahend: The number we're subtracting (bottom number)
• Difference: The result of subtraction
Regrouping helps us solve problems like 523 - 287 where we can't subtract 8 from 3 in the tens place. We borrow 1 hundred from the hundreds place, making it 4 hundreds, and add 10 tens to the tens place.
Key Concept
Regrouping means moving value from one place to another. When we can't subtract, we borrow 10 from the next left column.
How to Subtract with Regrouping
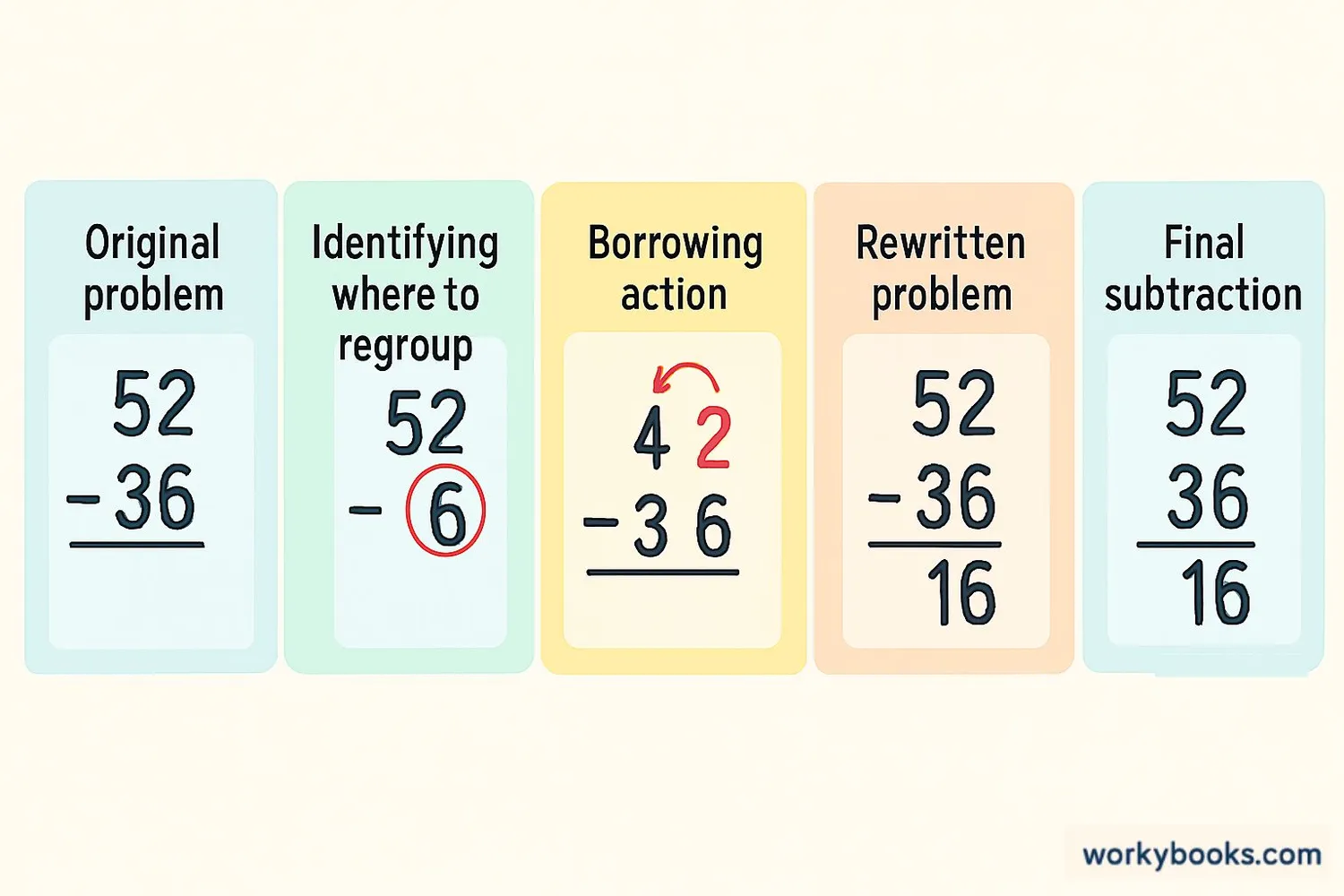
Follow these steps to solve 3-digit subtraction problems with regrouping:
Step-by-Step Method
- Write the numbers vertically with the minuend on top and subtrahend below, aligning by place value.
- Start subtracting from the right (ones place). If the top digit is smaller, regroup.
- To regroup: Take 1 from the next left column, add 10 to the current column, then subtract.
- Continue left through tens and hundreds places, regrouping when needed.
- Write the difference below each column after subtraction.
Example: 523 - 287
Answer: 236
Remember
Always check your work by adding the difference and subtrahend - it should equal the minuend!
Worked Examples

Let's practice with some examples:
Example 1: 642 - 379
- Write vertically: 642 over 379
- Ones place: 2 - 9 → can't do, regroup from tens
- 4 tens becomes 3 tens, 2 ones becomes 12 ones
- 12 - 9 = 3 (ones place)
- Tens place: 3 - 7 → can't do, regroup from hundreds
- 6 hundreds becomes 5 hundreds, 3 tens becomes 13 tens
- 13 - 7 = 6 (tens place)
- Hundreds place: 5 - 3 = 2
- Final answer: 263
Example 2: 805 - 467
- Write vertically: 805 over 467
- Ones place: 5 - 7 → can't do, need to regroup
- But tens place is 0, so we must regroup from hundreds first
- 8 hundreds becomes 7 hundreds, 0 tens becomes 10 tens
- Now regroup from tens to ones: 10 tens becomes 9 tens, 5 ones becomes 15 ones
- 15 - 7 = 8 (ones place)
- Tens place: 9 - 6 = 3
- Hundreds place: 7 - 4 = 3
- Final answer: 338
Practice Tip
When you have a zero in the tens place, you may need to regroup across two columns (from hundreds to tens, then from tens to ones).
Practice Quiz
Test your understanding with these 5 questions about 3-digit subtraction with regrouping:
Frequently Asked Questions
Common questions about subtraction with regrouping:
Math Trivia
Interesting facts about numbers and subtraction:
Ancient Subtraction
The ancient Egyptians used a form of subtraction that involved doubling numbers. They would subtract by adding up numbers that totaled the subtrahend, then seeing what was left from the minuend.
Number Systems
Not all number systems require regrouping for subtraction. The Roman numeral system, for example, uses a subtractive principle where IV means 4 (5-1) and IX means 9 (10-1).
Calculator History
The first mechanical calculator that could perform all four operations (including subtraction) was invented by Gottfried Wilhelm Leibniz in 1672. It used a stepped drum mechanism.
Subtraction Record
The largest subtraction problem ever solved on paper involved numbers with over 1 million digits each! It took mathematicians several days to verify the calculation.


