30 Degree Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn about angles in geometry with step-by-step guides, real-life examples, and practice activities
What is a 30 Degree Angle?

A 30 degree angle is an angle that measures exactly 30 degrees. It's one of the most common angles you'll encounter in geometry. Since 30 is less than 90, we call it an acute angle.
Imagine a full circle - it has 360 degrees. If you divide that circle into 12 equal parts, each part would be 30 degrees. This angle is exactly one-twelfth of a full circle!
Why is it important? 30-degree angles appear everywhere - in buildings, bridges, art, and nature. Understanding this angle helps us solve geometry problems and create accurate designs.
Key Concept
A 30-degree angle is an acute angle that measures exactly 30°, which is 1/12 of a full circle.
How to Construct a 30 Degree Angle
With a Protractor
1. Draw a straight line (AB) using a ruler.
2. Place the center of the protractor at point A.
3. Find the 30° mark on the protractor and make a dot.
4. Remove the protractor and draw a line from point A through the dot.
With Compass and Ruler
1. Draw a straight line (AB).
2. With A as center, draw an arc intersecting AB at C.
3. With C as center, draw another arc intersecting the first at D.
4. Draw a line from A through D - this creates a 60° angle.
5. Bisect this angle to get a 30° angle.
Remember
When using a compass, make sure the pencil is sharp and the compass is tight so your arcs are precise.
30 Degree Angle in Real Life
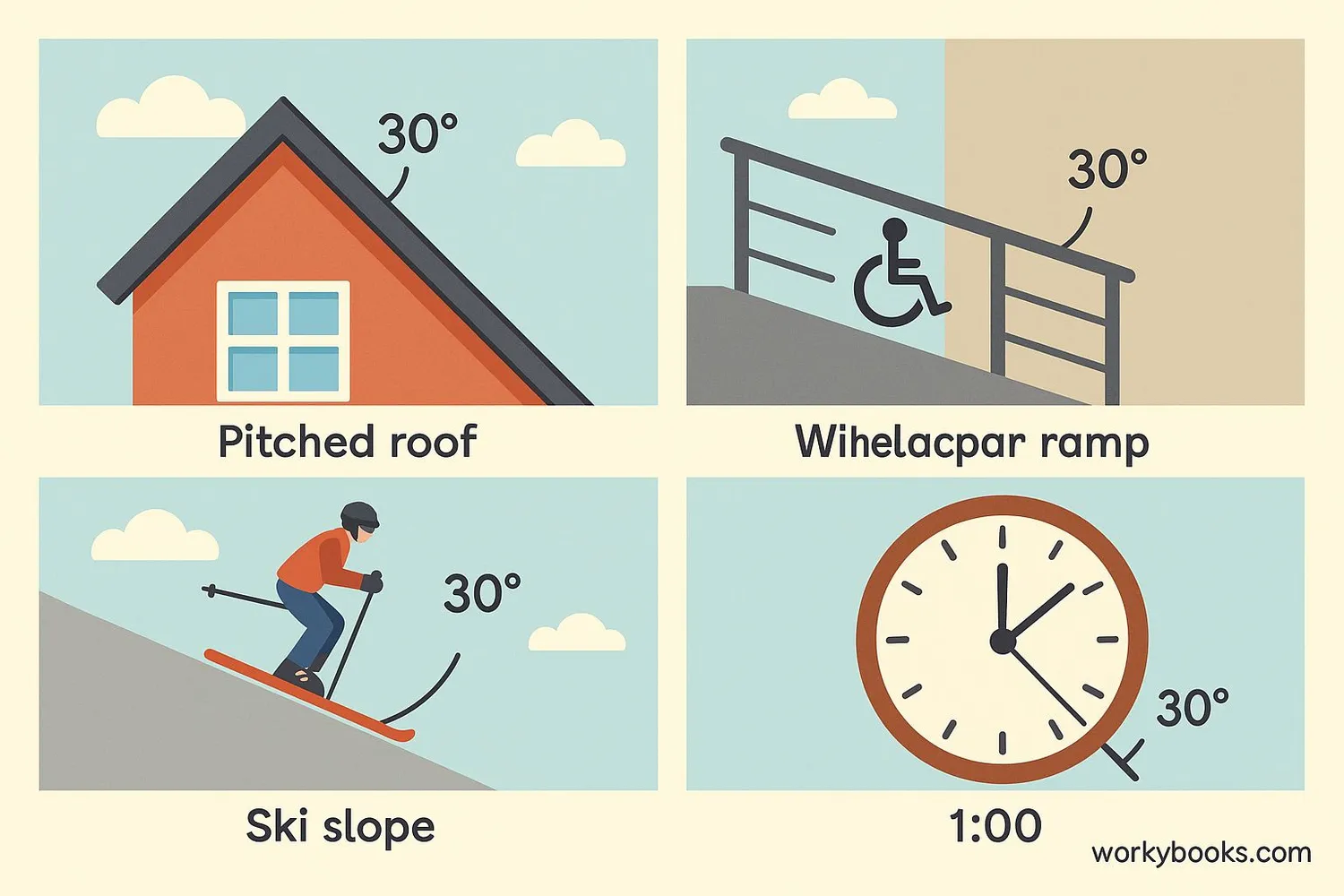
30-degree angles are all around us! Here are some common examples:
Roof Pitch: Many house roofs have a 30-degree slope to help rain and snow slide off easily.
Wheelchair Ramps: For safety, ramps are often built at a 30-degree angle to make them accessible but not too steep.
Ski Slopes: Beginner ski slopes have about a 30-degree incline - steep enough to slide but not too scary.
Clocks: At 1:00, the hour hand is at 30 degrees from the 12 o'clock position (since 360° ÷ 12 = 30° per hour).
Stairs: The ideal angle for a comfortable staircase is about 30 degrees.
Did You Know?
NASA space shuttles launched at about a 30-degree angle to gradually gain altitude while moving forward.
The 30-60-90 Triangle
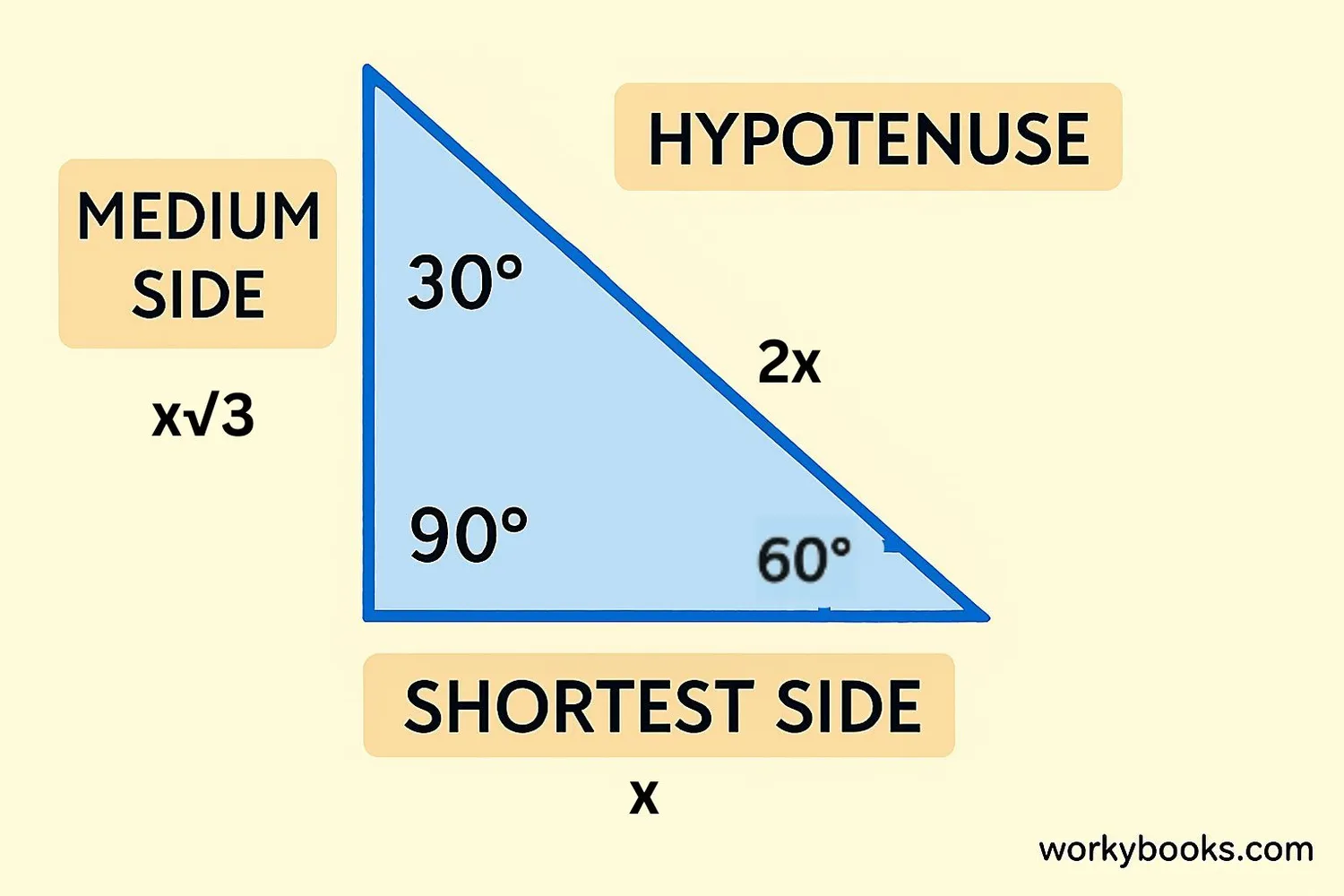
A 30-60-90 triangle is a special right triangle where the angles measure 30°, 60°, and 90°. What makes it special is the relationship between its sides:
Side Length Relationships
The side opposite the 30° angle is the smallest (x).
The side opposite the 60° angle is x√3.
The hypotenuse (opposite 90°) is 2x.
If the shortest side (opposite 30°) is 5 cm:
- Side opposite 60° = 5√3 ≈ 8.66 cm
- Hypotenuse = 2×5 = 10 cm
Remember
In a 30-60-90 triangle, the hypotenuse is always twice as long as the shortest side.
Angle Practice Quiz
Test your angle knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about 30-degree angles:
Angle Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Measurement
The Babylonians invented the degree system over 4,000 years ago! They chose 360 degrees for a full circle because 360 has many divisors, making calculations easier.
Nature's Angles
Honeybees build their honeycombs with precise 120-degree angles, creating perfect hexagons. This efficient design uses the least wax for the most storage space.
Space Angles
The Earth is tilted at 23.4 degrees relative to its orbit. This tilt creates our seasons! The Moon's orbit is tilted at about 5 degrees relative to Earth's orbit around the Sun.
Soccer Angles
Professional soccer players often kick the ball at 30-45 degree angles for maximum distance. The optimal angle for distance is 45 degrees, but players adjust for accuracy.


