60-Degree Angle - Definition, Examples, Quiz, FAQ, Trivia
Learn about this important geometric angle with simple explanations and practice activities
What is a 60-Degree Angle?
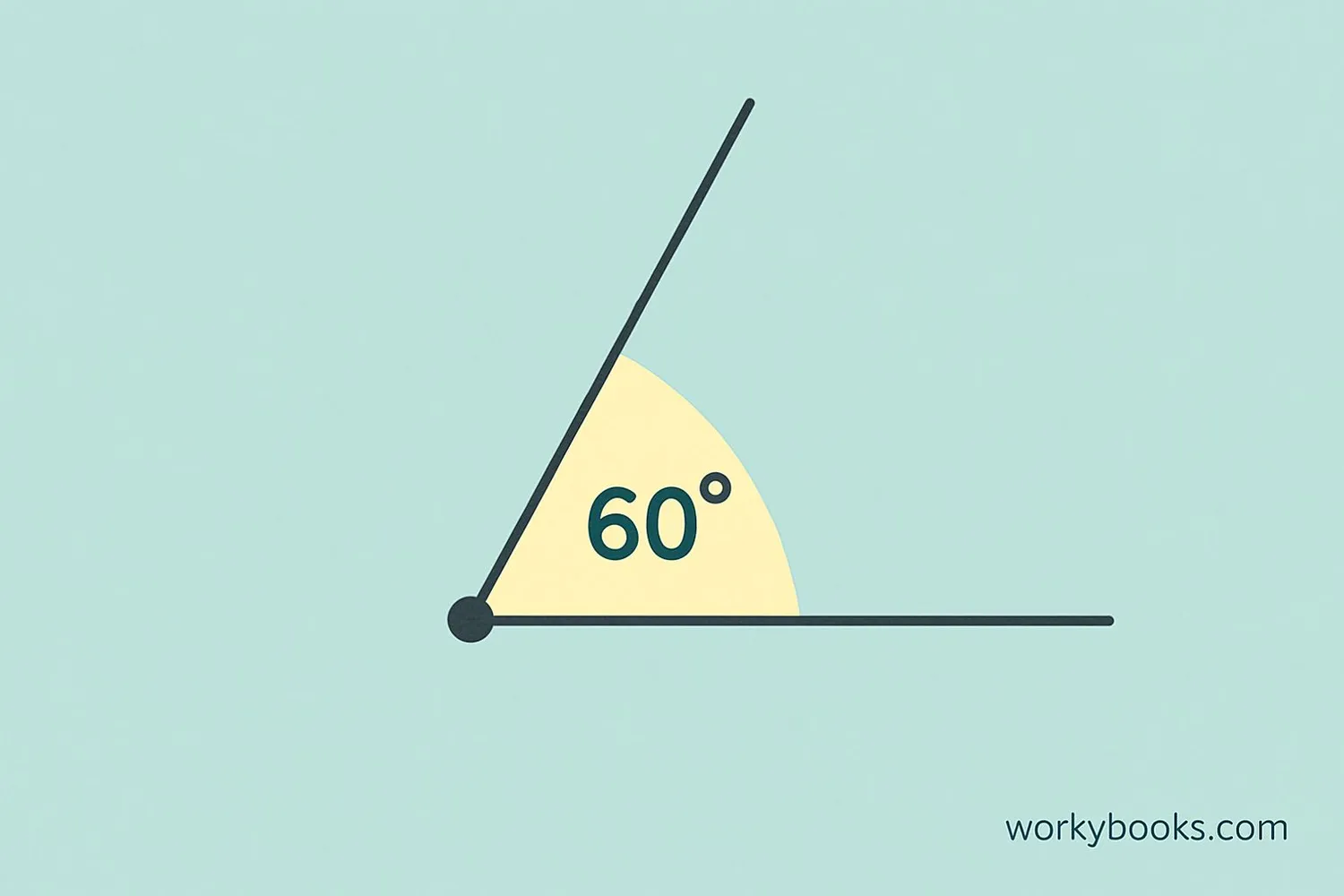
A 60-degree angle is an angle that measures exactly sixty degrees. It's an acute angle because it's less than 90 degrees.
Angles are measured in degrees using a protractor. A full circle has 360 degrees, so 60 degrees is one-sixth of a full circle.
The 60-degree angle is special because it appears in many geometric shapes:
- All three angles in an equilateral triangle are 60 degrees
- It's part of the 30-60-90 triangle which has special properties
- Six 60-degree angles fit perfectly around a point (6 × 60° = 360°)
Key Concept
60 degrees is an acute angle that appears frequently in geometry, especially in equilateral triangles and regular hexagons.
How to Construct a 60-Degree Angle

You can create a perfect 60-degree angle using just a compass and straightedge. Here's how:
Draw a straight line (AB) with your ruler
Place compass point on A, draw an arc crossing AB
Without changing compass width, place point where arc crosses AB and draw another arc
Draw a line from A through where arcs intersect
The angle between AB and the new line is exactly 60 degrees! This method works because you're creating an equilateral triangle, where all angles are 60 degrees.
Remember
Constructing a 60-degree angle is the first step in creating an equilateral triangle, one of the most perfect shapes in geometry.
Properties of 60-Degree Angles
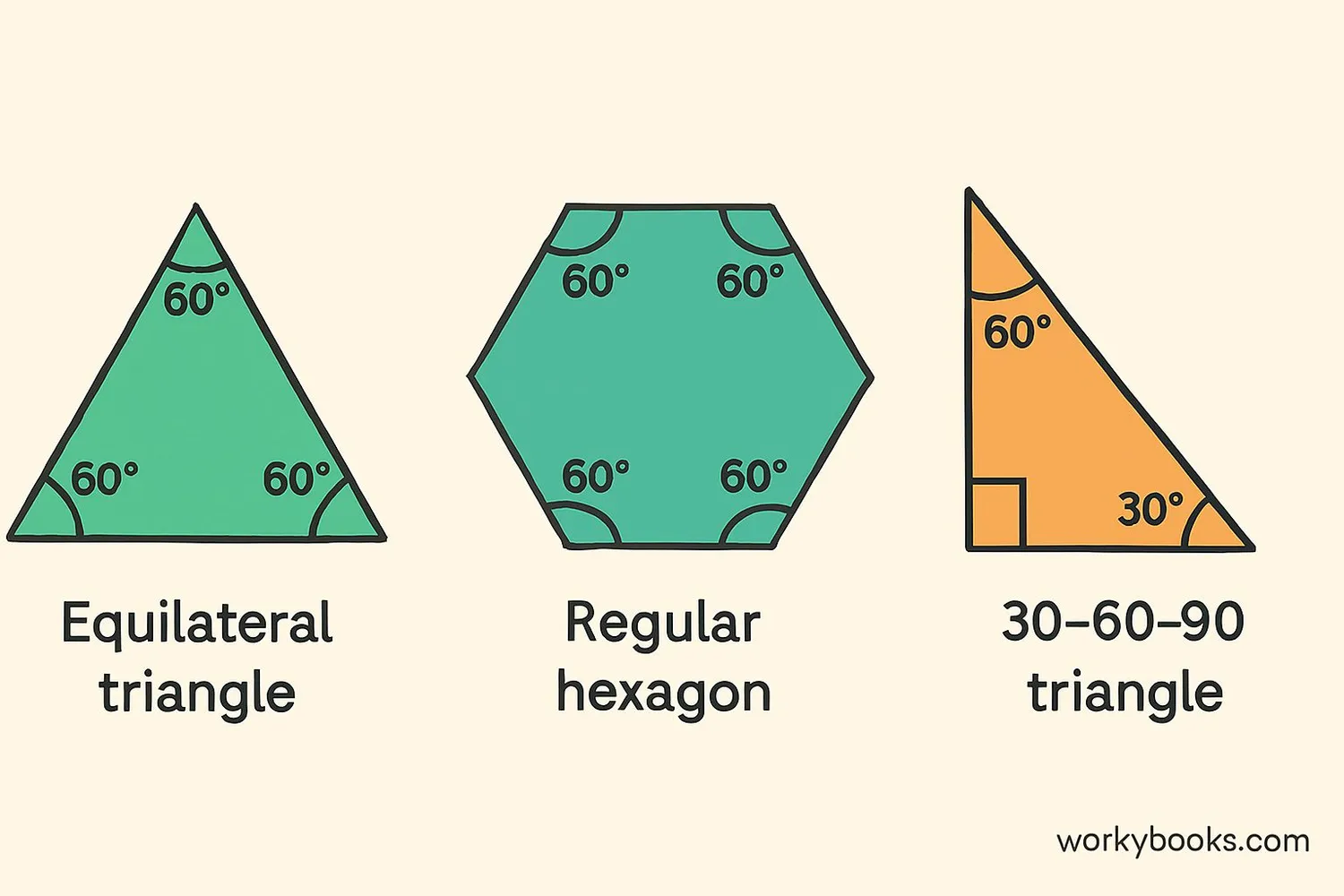
60-degree angles have special properties that make them important in geometry:
In Equilateral Triangles
All three angles in an equilateral triangle are exactly 60 degrees. This is because the sum of angles in any triangle is 180 degrees, and 180 ÷ 3 = 60.
In Regular Hexagons
A regular hexagon has six 60-degree angles at its center. Each internal angle is 120 degrees, but the central angles between vertices are all 60 degrees.
In 30-60-90 Triangles
This special right triangle has angles of 30°, 60°, and 90°. The sides have a consistent ratio: the side opposite 30° is x, opposite 60° is x√3, and the hypotenuse is 2x.
| Shape | Role of 60° Angle | Special Properties |
|---|---|---|
| Equilateral Triangle | All three angles | All sides equal, all angles equal |
| Regular Hexagon | Central angles | Six equal sides, tessellates perfectly |
| 30-60-90 Triangle | Middle-sized angle | Sides ratio 1 : √3 : 2 |
Math Fact
60 degrees is equal to π/3 radians. Radians are another way to measure angles used in advanced mathematics.
Real-World Examples
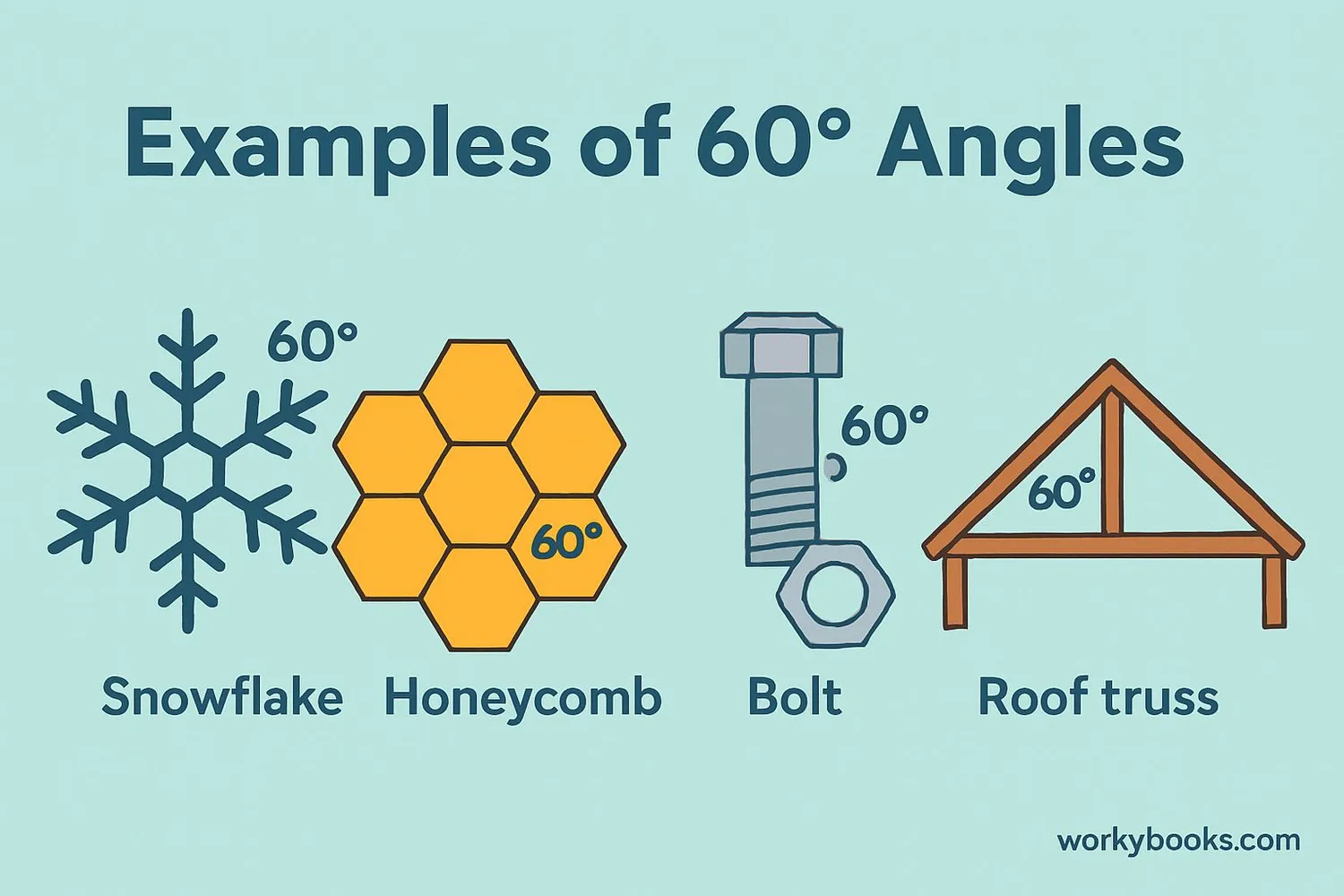
60-degree angles appear all around us in both nature and human design:
In Nature
- Snowflakes: Many snowflakes have hexagonal symmetry with 60-degree angles
- Honeycombs: Bees build hexagonal honeycombs with 60-degree angles
- Crystal structures: Some minerals form with 60-degree angles
In Human Design
- Bolts and nuts: Many have hexagonal heads with 60-degree angles
- Roof trusses: Often use equilateral triangles for strength
- Tiling patterns: Hexagonal tiles fit together with 60-degree angles
- Traffic signs: Some warning signs use equilateral triangles
Observation Tip
Next time you see a bolt or a honeycomb, look for the 60-degree angles. They're all around you!
Angle Knowledge Quiz
Test your understanding of 60-degree angles with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about 60-degree angles:
Geometry Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Masters
The ancient Babylonians first divided circles into 360 degrees around 1800 BCE. They chose 360 because it has many divisors, making calculations easier.
Nature's Geometry
Many flowers arrange their petals and seeds using angles based on the golden angle (approximately 137.5°), which is derived from the golden ratio.
Architectural Angles
The famous architect Buckminster Fuller used 60-degree angles in his geodesic domes, creating incredibly strong structures using triangles.
Hexagon Perfection
Regular hexagons can tile a plane perfectly with no gaps because their internal angles (120°) and external angles (60°) fit together seamlessly.





