Least Common Denominator (LCD) - Definition, Examples, Quiz, FAQ, Trivia
Learn to find the least common denominator with easy explanations, examples, and practice activities
What is the Least Common Denominator?
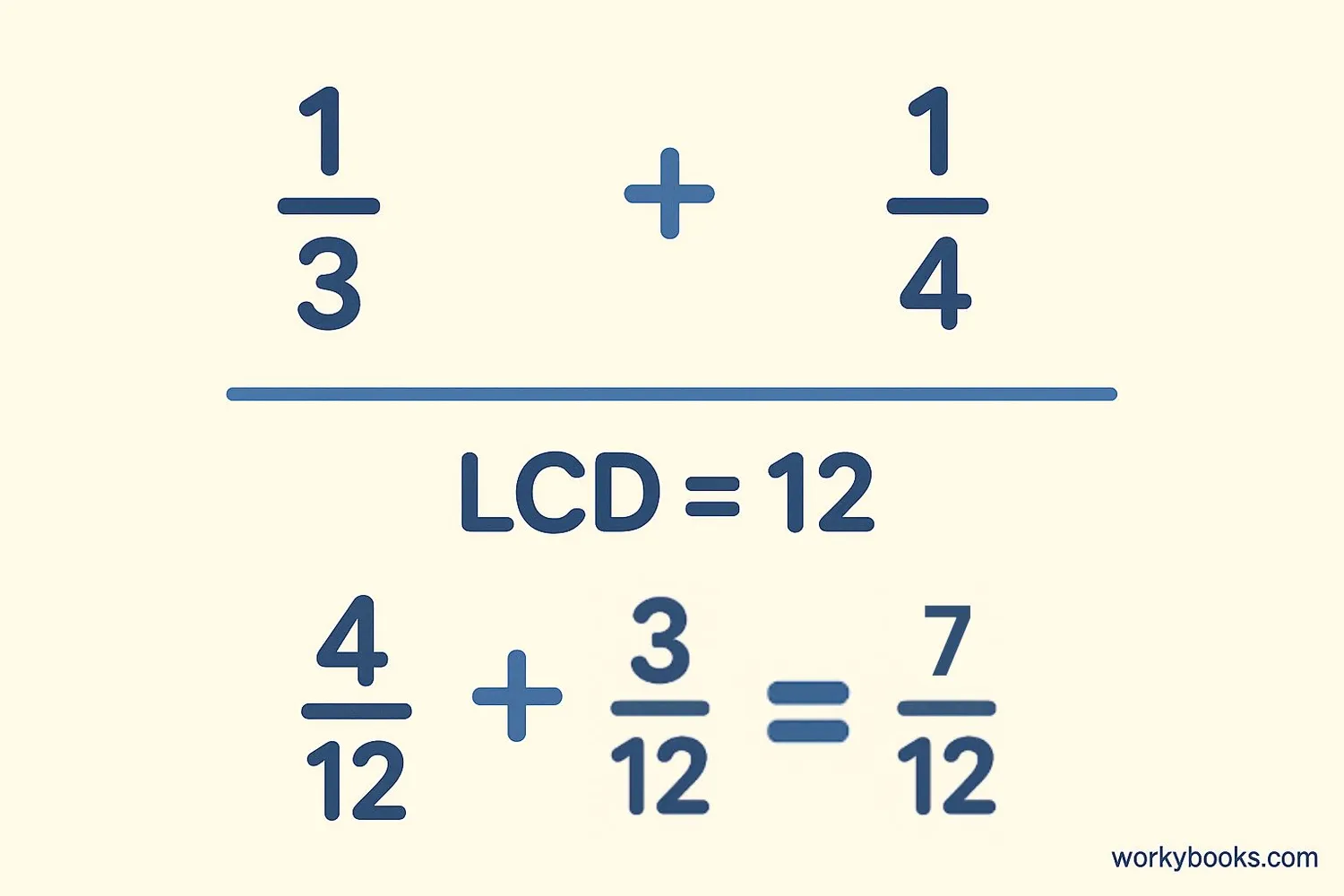
The Least Common Denominator (LCD) is the smallest number that can be used as a common denominator for a set of fractions. It helps us add, subtract, or compare fractions that have different denominators.
Think of it like finding a common language for fractions that speak different "denominator languages." The LCD is the smallest common language they all understand.
The LCD is actually the Least Common Multiple (LCM) of the denominators. For example, for the fractions 1/3 and 1/4, the denominators are 3 and 4. The multiples of 3 are 3, 6, 9, 12, 15... and the multiples of 4 are 4, 8, 12, 16... The smallest common multiple is 12, so the LCD is 12.
Key Concept
The Least Common Denominator (LCD) is the smallest number that all denominators can divide into evenly. It's the LCM of the denominators.
How to Find the Least Common Denominator

There are several methods to find the Least Common Denominator. Here are the two most common methods:
Method 1: Listing Multiples
List the multiples of each denominator
Find the smallest multiple that appears in all lists
This number is your LCD
Method 2: Prime Factorization
Find the prime factors of each denominator
Take the highest power of each prime factor that appears
Multiply these together to get the LCD
LCD Formula
The Least Common Denominator is the Least Common Multiple of all the denominators.
Remember
Once you find the LCD, you can convert all fractions to equivalent fractions with that denominator, making them easier to work with.
Examples of Finding LCD

Let's practice finding the LCD with some examples:
Example 1: Find the LCD for 1/2 and 1/3
Step 1: Denominators are 2 and 3
Step 2: Multiples of 2: 2, 4, 6, 8, 10...
Step 3: Multiples of 3: 3, 6, 9, 12, 15...
Step 4: The smallest common multiple is 6
Solution: LCD = 6
Example 2: Find the LCD for 2/5 and 3/4
Step 1: Denominators are 5 and 4
Step 2: Multiples of 5: 5, 10, 15, 20, 25...
Step 3: Multiples of 4: 4, 8, 12, 16, 20, 24...
Step 4: The smallest common multiple is 20
Solution: LCD = 20
Example 3: Find the LCD for 1/4, 1/6, and 1/8
Step 1: Denominators are 4, 6, and 8
Step 2: Multiples of 4: 4, 8, 12, 16, 20, 24, 28...
Step 3: Multiples of 6: 6, 12, 18, 24, 30, 36...
Step 4: Multiples of 8: 8, 16, 24, 32, 40...
Step 5: The smallest common multiple is 24
Solution: LCD = 24
Practice Tip
When working with larger numbers, prime factorization is often the faster method to find the LCD.
LCD Practice Quiz
Test your understanding of least common denominators with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about least common denominators:
Math Trivia
Discover interesting facts about fractions and denominators:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they primarily used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fractions in Nature
Many patterns in nature follow fractional relationships. For example, the arrangement of leaves on a stem often follows fractions from the Fibonacci sequence, which helps maximize sunlight exposure.
Fractions in Music
Musical rhythms are based on fractions. A whole note gets 4 beats, a half note gets 2 beats, a quarter note gets 1 beat, and so on. Musicians use these fractions to read and play music accurately.
The Largest Denominator
In theory, there's no limit to how large a denominator can be. However, the practical limit depends on what we're measuring. In most real-world applications, we rarely need denominators larger than 100.





