(A + B)3 Formula - Definition, Examples, Quiz, FAQ, Trivia
Learn the algebraic identity for the cube of a binomial sum with visual explanations and practice activities
What is (A + B)3?
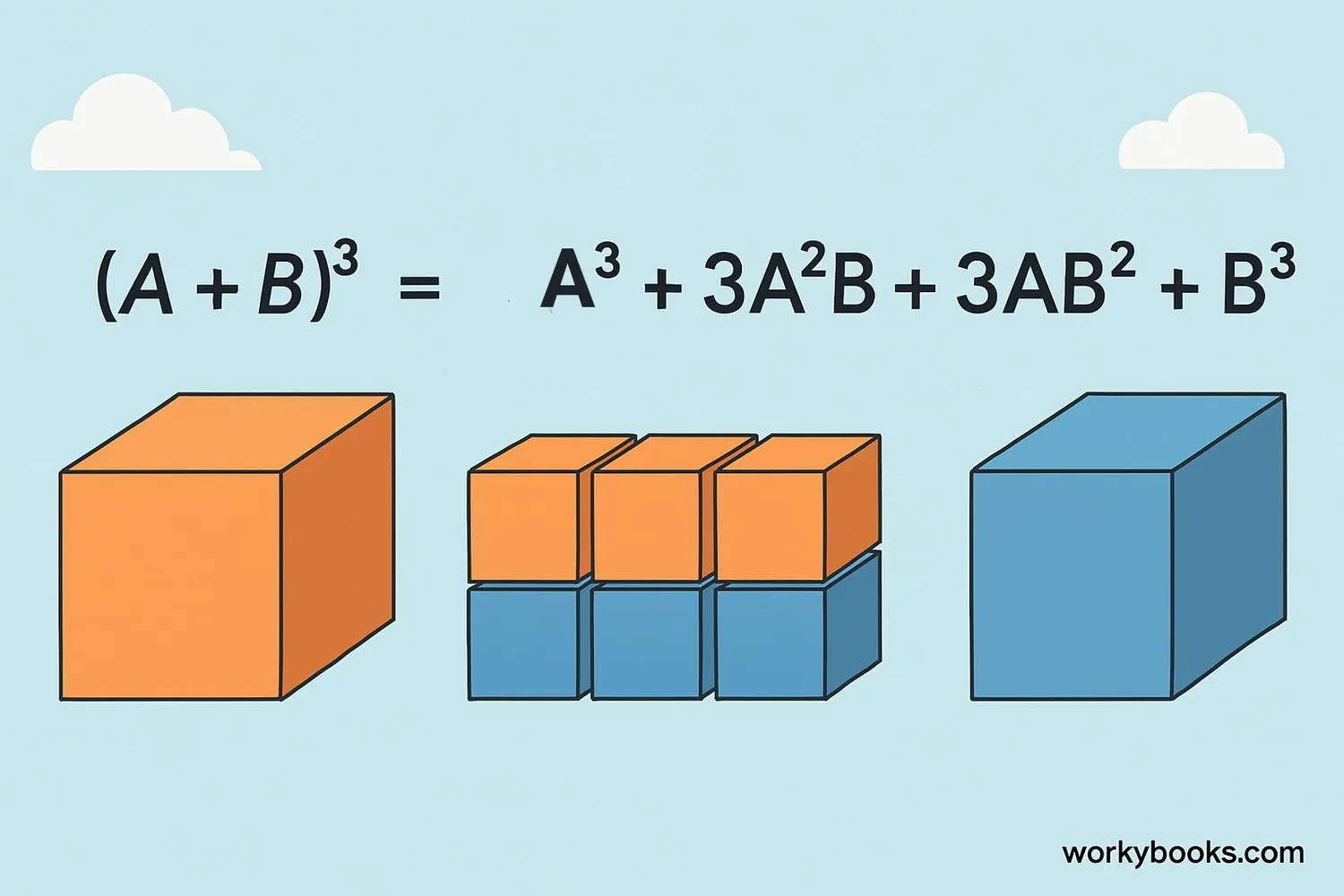
The expression (A + B)3 means multiplying (A + B) by itself three times. This is called the "cube of a binomial" since it involves two terms (A and B) being cubed.
Understanding this formula helps us quickly expand expressions without having to multiply everything step-by-step. It's like having a math shortcut!
The formula for (A + B)3 is:
This identity shows us how to expand any binomial expression raised to the third power. Notice the pattern: the exponents of A decrease while exponents of B increase.
Key Concept
A binomial is an algebraic expression with two terms. The cube of a binomial has four terms in its expanded form.
The (A + B)3 Formula

The standard formula for (A + B)3 is:
Algebraic Identity
This formula helps us expand binomial expressions quickly without multiplication.
- A3 - Cube of the first term
- 3A2B - Three times the square of A multiplied by B
- 3AB2 - Three times A multiplied by the square of B
- B3 - Cube of the second term
The coefficients (1, 3, 3, 1) follow the third row of Pascal's Triangle. Remember that any number raised to the power of 0 is 1, so we can write the coefficients as:
Remember
The formula for (A + B)3 always has four terms, and the coefficients are always 1, 3, 3, 1 in that order.
Derivation of the Formula

We can derive the (A + B)3 formula by multiplying step-by-step:
Step 1: Start with (A + B)3 = (A + B) × (A + B) × (A + B)
Step 2: First multiply two binomials: (A + B) × (A + B) = A2 + 2AB + B2
Step 3: Now multiply this result by (A + B):
Step 4: Distribute each term:
Step 5: Simplify:
Step 6: Combine like terms:
And we've derived the formula! This shows why (A + B)3 equals A3 + 3A2B + 3AB2 + B3.
Pattern Recognition
Notice how the exponents of A decrease from 3 to 0 while exponents of B increase from 0 to 3? This pattern continues for higher powers too!
Examples and Applications
Let's practice using the formula with some examples:
Example 1
Expand (x + 2)3
Example 2
Expand (2y + 3)3
Example 3
Expand (3a + b)3
Example 4
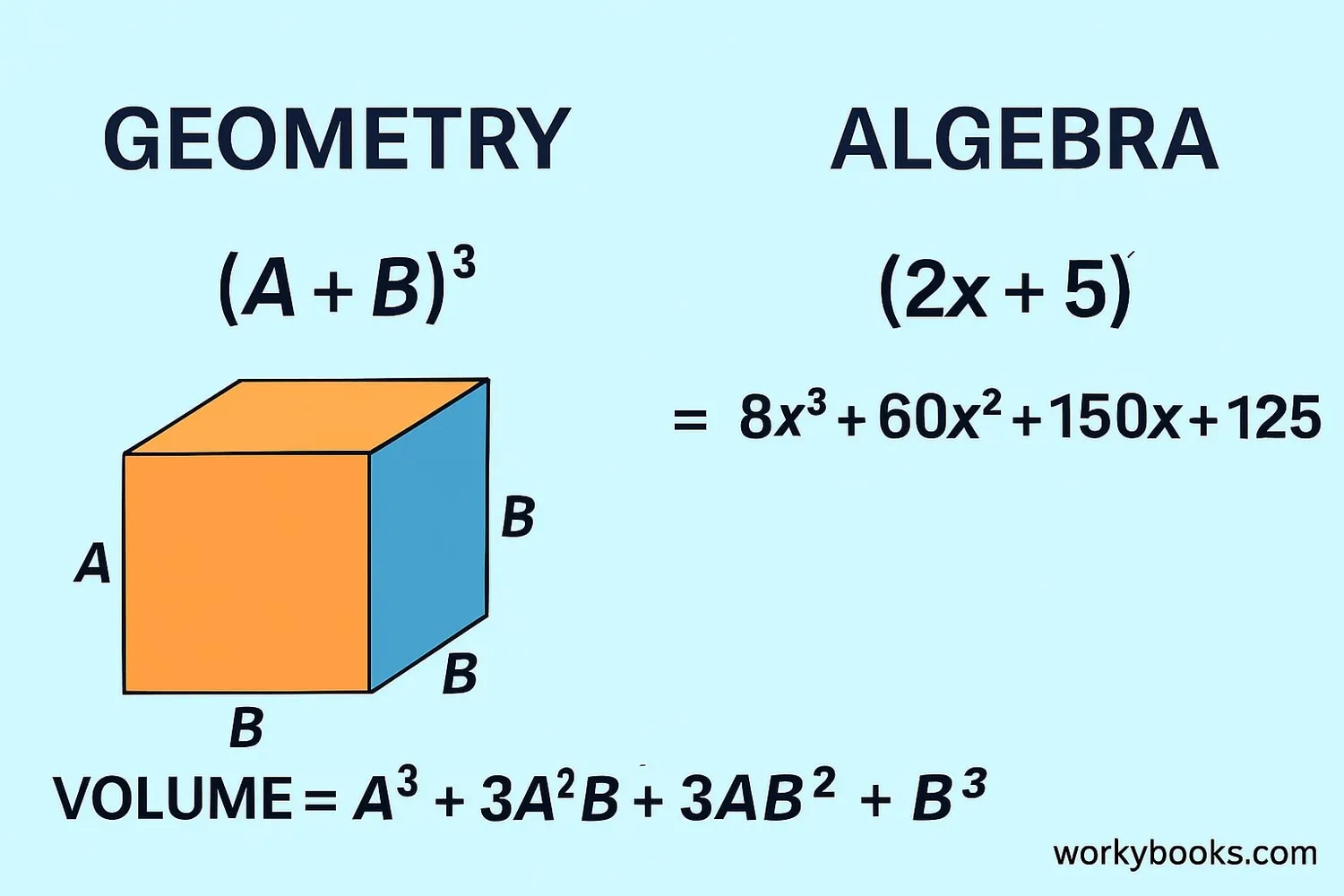
Volume Application
If a cube has sides of length (x + 2), its volume is (x + 2)3. Using our formula:
Application Tip
This formula is especially useful in geometry for calculating volumes and in algebra for polynomial expansion.
Practice Quiz
Test your understanding of the (A + B)3 formula with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about the (A + B)3 formula:
Math Trivia
Discover interesting facts about algebra and formulas:
Ancient Origins
The binomial theorem was known to mathematicians in ancient India and Persia as early as the 10th century. The Persian mathematician Al-Karaji described the triangular pattern of binomial coefficients around 1000 AD.
Pascal's Contribution
While Pascal didn't discover the triangle named after him, his 1653 treatise organized and demonstrated so many properties of the triangle that it became associated with his name. The triangle provides coefficients for binomial expansions.
Calculator Connection
The binomial theorem is used in calculators and computers to compute powers and roots of numbers. The expansion allows efficient approximation of complex calculations.
Beyond Cubes
The binomial theorem can be extended to any positive integer power. For (A+B)n, there will be (n+1) terms with coefficients from the nth row of Pascal's Triangle.




