A Intersection B Complement - Definition, Examples, Quiz, FAQ, Trivia
Learn about set differences with easy explanations, Venn diagrams, examples, and practice activities
What is A ∩ B'?
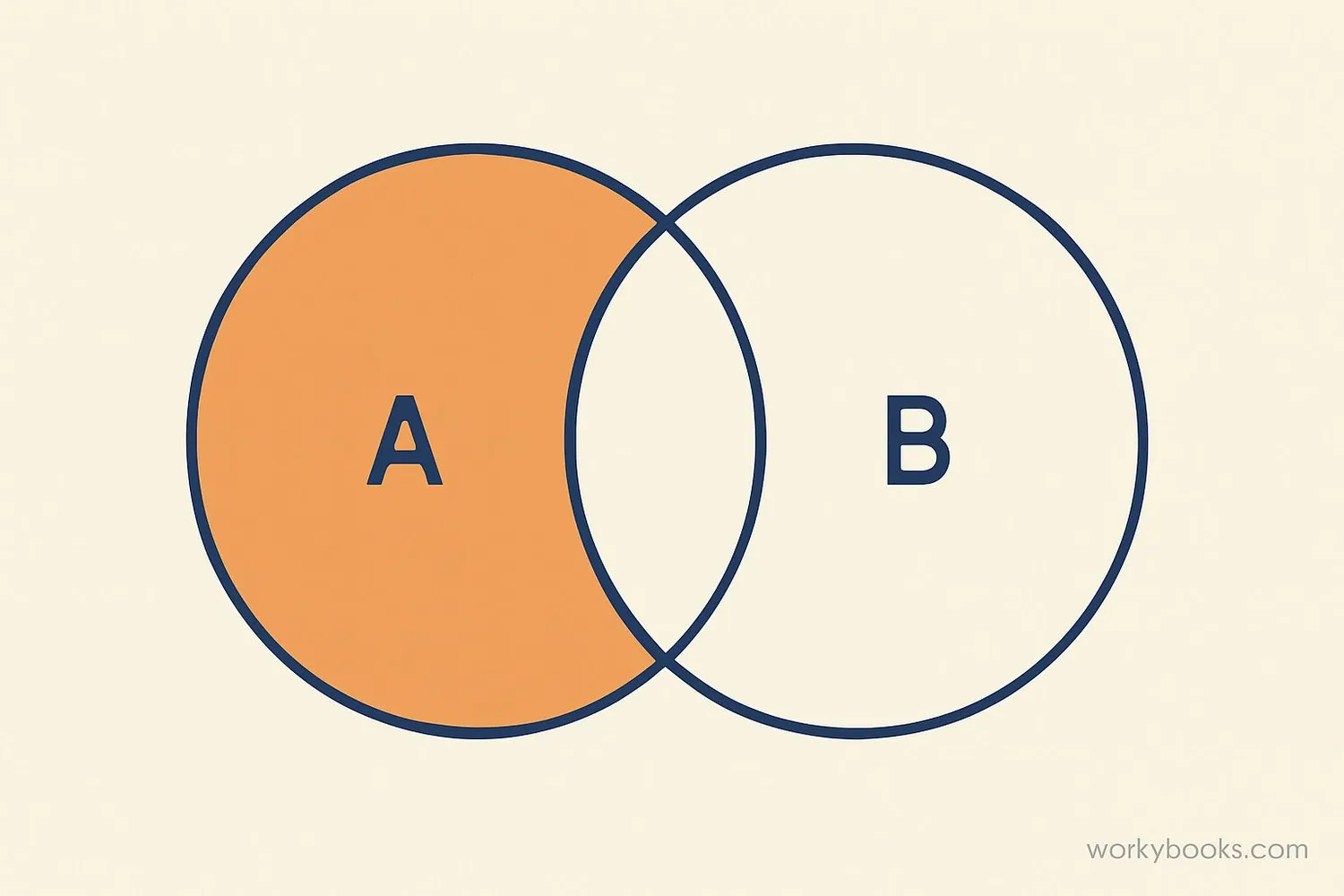
A ∩ B' (pronounced "A intersection B complement") represents all the elements that are in set A but not in set B.
Think of it like this:
- A is your favorite fruits: apples, bananas, cherries
- B is fruits that are red: apples, cherries, strawberries
- A ∩ B' would be fruits that are your favorites but NOT red → bananas
In set theory, we call this the "relative complement" or "set difference." It's written as A - B or A \ B. The complement of B (B') includes everything that is not in B.
Mathematical Definition
This means: A ∩ B' contains all elements x that belong to A but do not belong to B.
Key Concept
A ∩ B' answers the question: "What is in A that is NOT in B?"
How to Find A ∩ B'
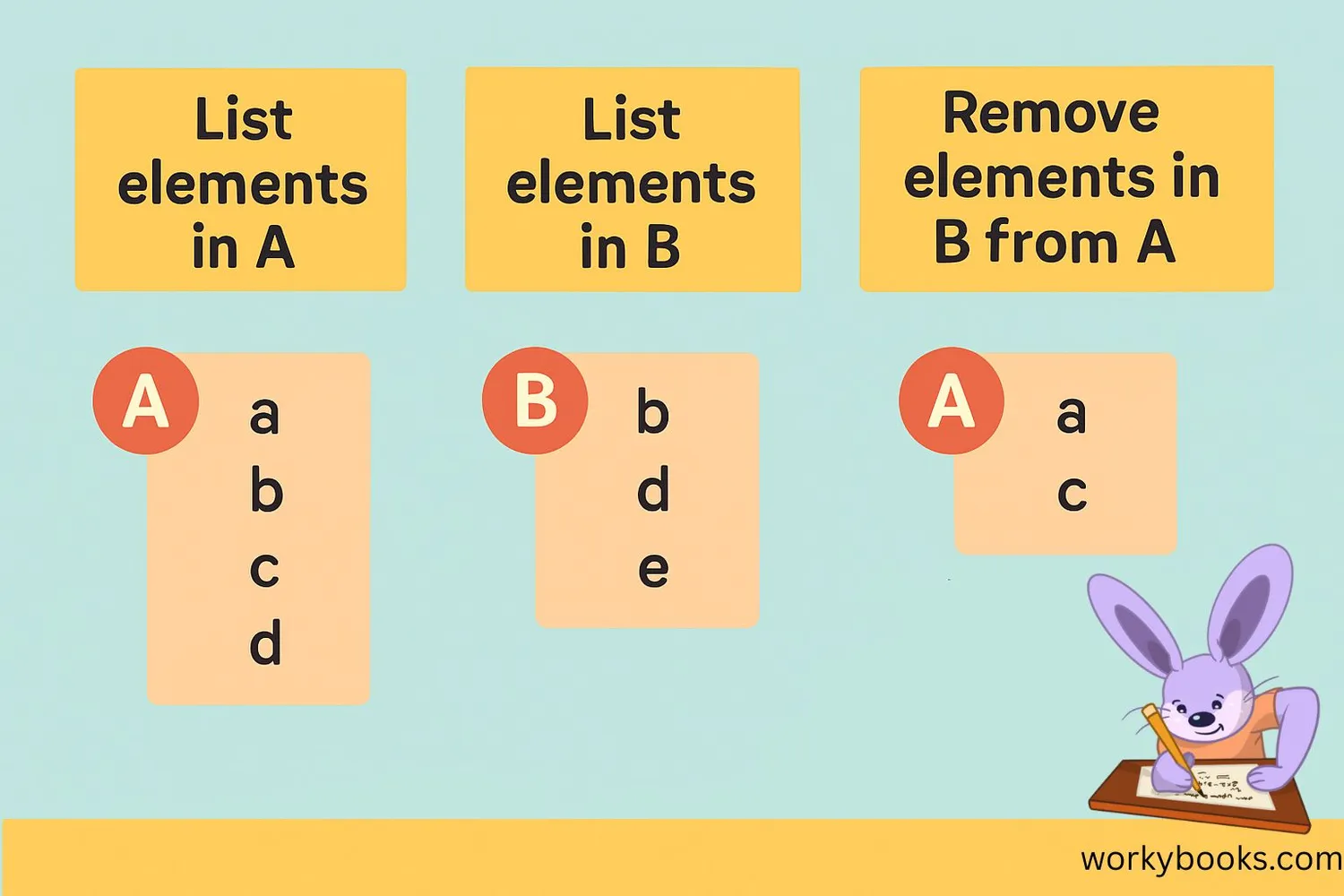
Finding A ∩ B' is straightforward when you follow these steps:
Step 1: Identify all elements in set A
Step 2: Identify all elements in set B
Step 3: From set A, remove any elements that are also in set B
Let's practice with an example:
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7}
Solution:
Elements in A: 1, 2, 3, 4, 5
Elements in B: 4, 5, 6, 7
Elements in both A and B: 4, 5
A ∩ B' = {1, 2, 3}
Remember
A ∩ B' is different from B ∩ A' (which would be elements in B but not in A).
Venn Diagrams
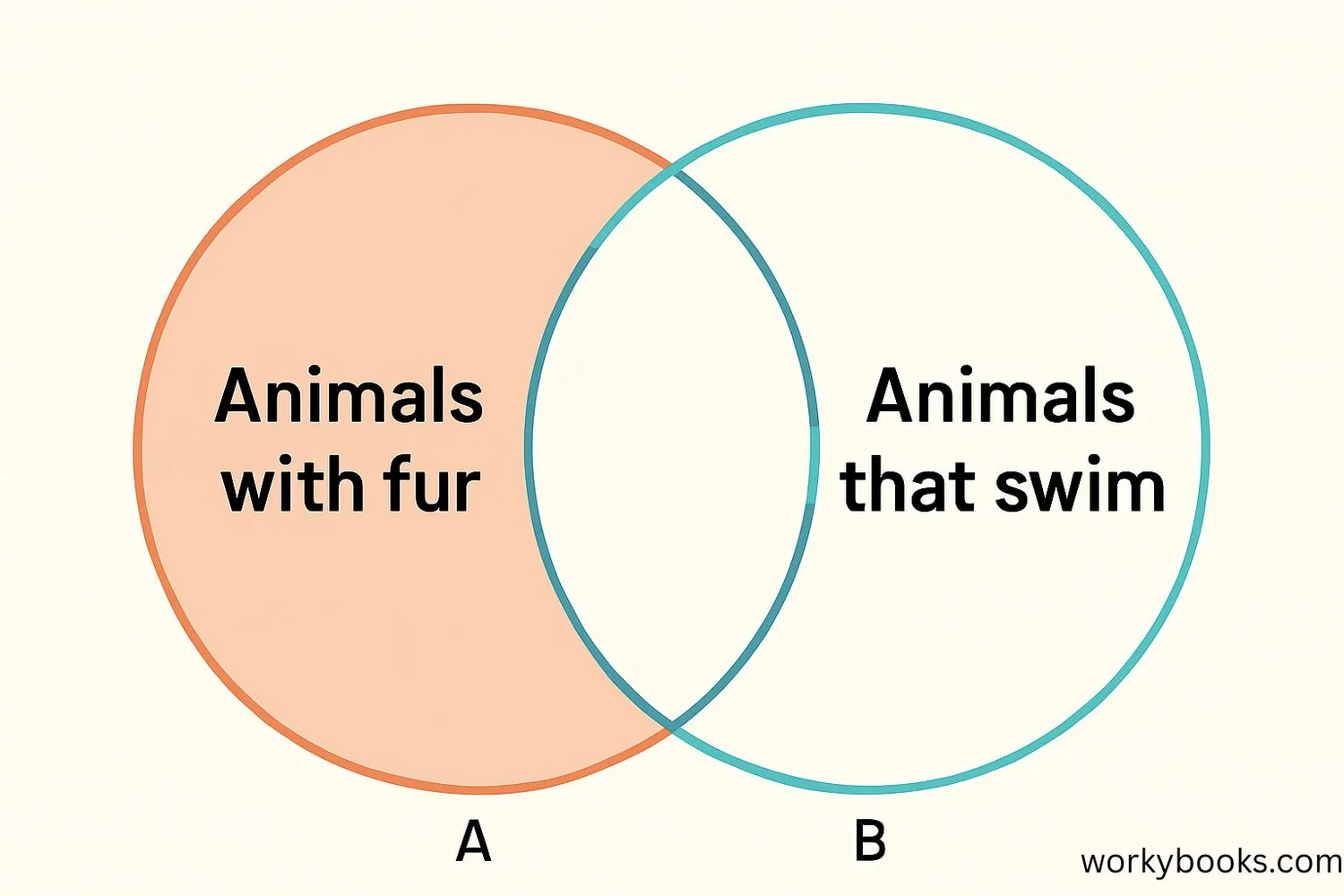
Venn diagrams are perfect for visualizing set operations like A ∩ B'. Here's how it works:
Parts of a Venn diagram:
- The rectangle represents the universal set (all possible elements)
- Circle A represents all elements in set A
- Circle B represents all elements in set B
- The overlapping region represents A ∩ B (elements in both A and B)
Visualizing A ∩ B':
A ∩ B' is represented by the part of circle A that does NOT overlap with circle B. This region is only in A, not in B.
Real-World Example
A: Students who like math
B: Students who like science
A ∩ B': Students who like math but not science
Diagram Tip
When drawing Venn diagrams, A ∩ B' is always the crescent-shaped part of circle A that doesn't touch circle B.
Examples

Let's look at some examples to understand A ∩ B' better:
Example 1:
A = {Cat, Dog, Fish, Bird} (house pets)
B = {Fish, Turtle, Frog} (pets that live in water)
A ∩ B' = {Cat, Dog, Bird} (house pets that don't live in water)
Example 2:
A = {2, 4, 6, 8, 10} (even numbers)
B = {3, 6, 9, 12} (multiples of 3)
A ∩ B' = {2, 4, 8, 10} (even numbers not divisible by 3)
Example 3:
A: People with brown hair
B: People with glasses
A ∩ B': People with brown hair who don't wear glasses
Example 4:
A: Foods that are fruits
B: Foods that are red
A ∩ B': Fruits that are not red (bananas, oranges, etc.)
Practice Tip
Look around you - can you find examples of A ∩ B' in your classroom, home, or neighborhood?
Practice Quiz
Test your understanding of A ∩ B' with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about A ∩ B':
Set Theory Trivia
Discover interesting facts about set theory:
Origin of Set Theory
Set theory was created by Georg Cantor in the 1870s. He was studying mathematical infinity when he developed the concept of sets, which became the foundation of modern mathematics.
Sets in Computers
Computers use set operations every day! When you search for "cats NOT dogs" online, the search engine is using A ∩ B' where A is cat pages and B is dog pages.
Sets in Space
NASA uses set theory to calculate spacecraft trajectories. They define sets of possible paths and use operations like intersection and complement to find the best route.
Largest Set Collection
The largest collection of distinct sets in mathematics is unimaginably huge! The set of all possible sets leads to interesting paradoxes that mathematicians still study today.





