Absolute Value - Definition, Examples, Quiz, FAQ, Trivia

What is Absolute Value?

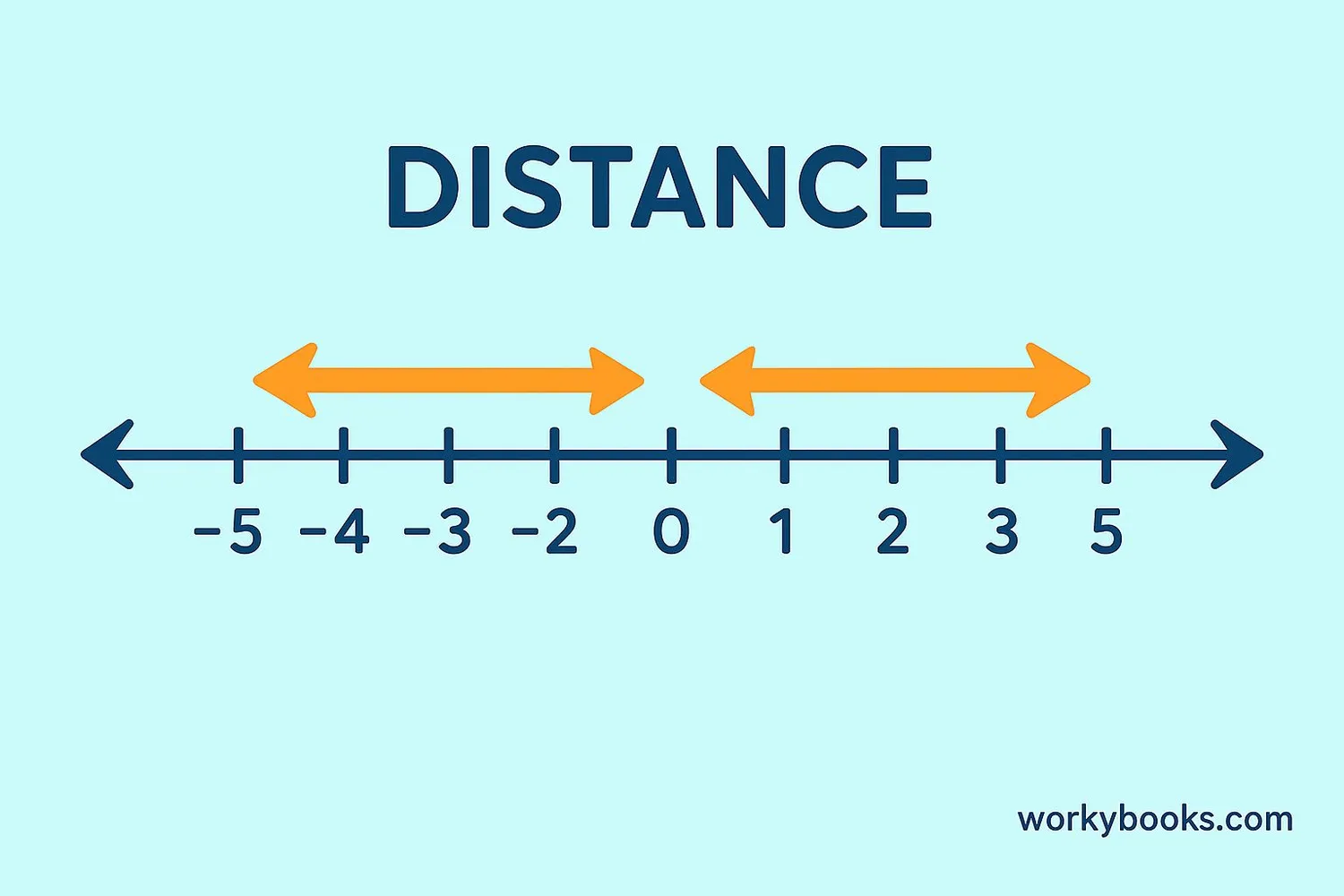
Absolute value is a special math idea that tells us how far a number is from zero on the number line. It doesn't matter if the number is positive or negative - we only care about how far it is from zero.

Think of it like measuring distance: whether you walk 5 steps left or 5 steps right from your starting point, you've still walked 5 steps. Absolute value works the same way with numbers!

The absolute value of a number is always positive or zero. It's never negative because distance can't be negative.

Absolute Value Symbol

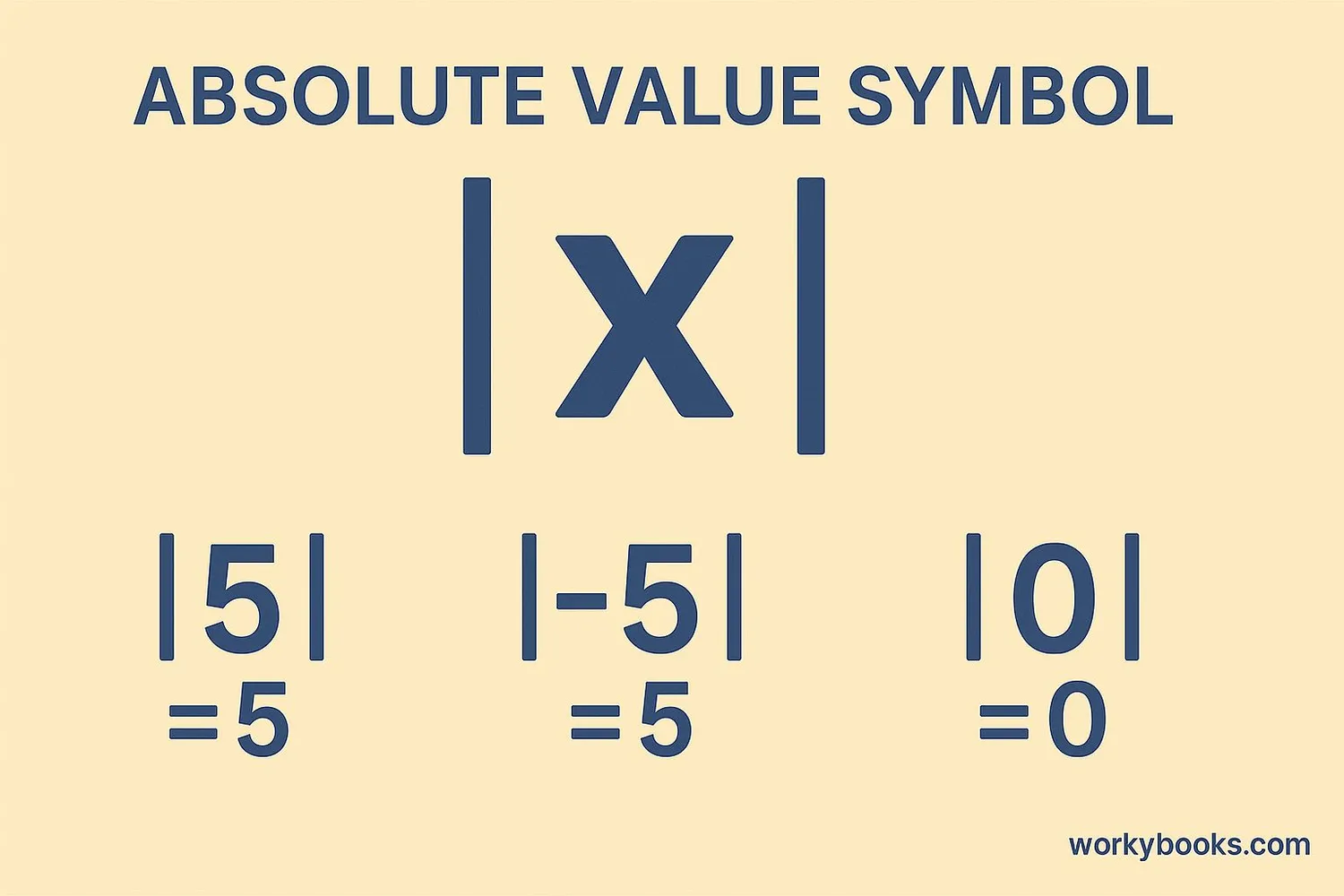
We write absolute value using two vertical bars around a number, like this: |number|. For example:

• |5| = 5 (5 is 5 units from zero)
• |-5| = 5 (-5 is also 5 units from zero)
• |0| = 0 (zero is zero units from itself)
• |3.2| = 3.2
• |-7| = 7

Absolute Value on a Number Line

The number line is the best way to understand absolute value. Let's look at some examples:

In the number line above:

• Both 2 and -2 are exactly 2 units away from zero
• So |2| = 2 and |-2| = 2
• The green lines show the distance being measured

This visual helps us see that absolute value is about distance, not direction.

Absolute Value Properties

Absolute value has some special math properties that are always true:

1. Non-negativity: |x| ≥ 0 for any number x
Absolute value is never negative - it's always positive or zero.

2. Positive definiteness: |x| = 0 only when x = 0
The only number with absolute value zero is zero itself.

3. Multiplicativity: |x × y| = |x| × |y|
The absolute value of a product is the product of absolute values.

4. Subadditivity: |x + y| ≤ |x| + |y|
The absolute value of a sum is less than or equal to the sum of absolute values.

Real-World Examples

Absolute value isn't just for math class - we use it in real life too! Here are some examples:

Temperature: When we say it's -5°C outside, the absolute value | -5 | = 5 tells us how cold it is without worrying about the negative sign.

Elevation: If a location is 50 meters below sea level, we write it as -50 meters. The absolute value | -50 | = 50 tells us how deep it is.

Distance: If you walk 3 blocks east and then 3 blocks west, your position hasn't changed, but you've walked a total distance of |3| + | -3 | = 6 blocks.

Finance: If you owe $20 (which is -20 dollars), the absolute value | -20 | = 20 tells how much money you owe without the negative sign.

Absolute Value Quiz

Test your understanding with this 5-question quiz. Choose the correct answer for each question.

Frequently Asked Questions

Here are answers to common questions about absolute value:

Math Trivia

Discover interesting facts about numbers and absolute value: