Adding Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn to add fractions with easy explanations, visual models, and practice activities
What Are Fractions?

Fractions represent parts of a whole. When we have a whole object and we divide it into equal parts, each part is a fraction of the whole.
Fractions are used in cooking, measuring, telling time, and many other everyday situations. Understanding fractions helps us describe parts of things accurately.
The word "fraction" comes from the Latin word "fractus" meaning "broken." Fractions help us work with quantities that are not whole numbers.
Key Concept
A fraction has two parts: the numerator (top number) tells how many parts we have, and the denominator (bottom number) tells how many equal parts make a whole.
Parts of a Fraction
Denominator (4): Total equal parts in the whole
Every fraction has two important parts:
Numerator: The top number that tells how many parts we have or are considering.
Denominator: The bottom number that tells how many equal parts the whole is divided into.
Think of a pizza cut into 8 equal slices. If you have 3 slices, your fraction is ³⁄₈. The numerator is 3 (slices you have) and the denominator is 8 (total slices in the whole pizza).
Remember
The denominator can never be zero because you can't divide something into zero parts!
Adding Fractions with Same Denominator
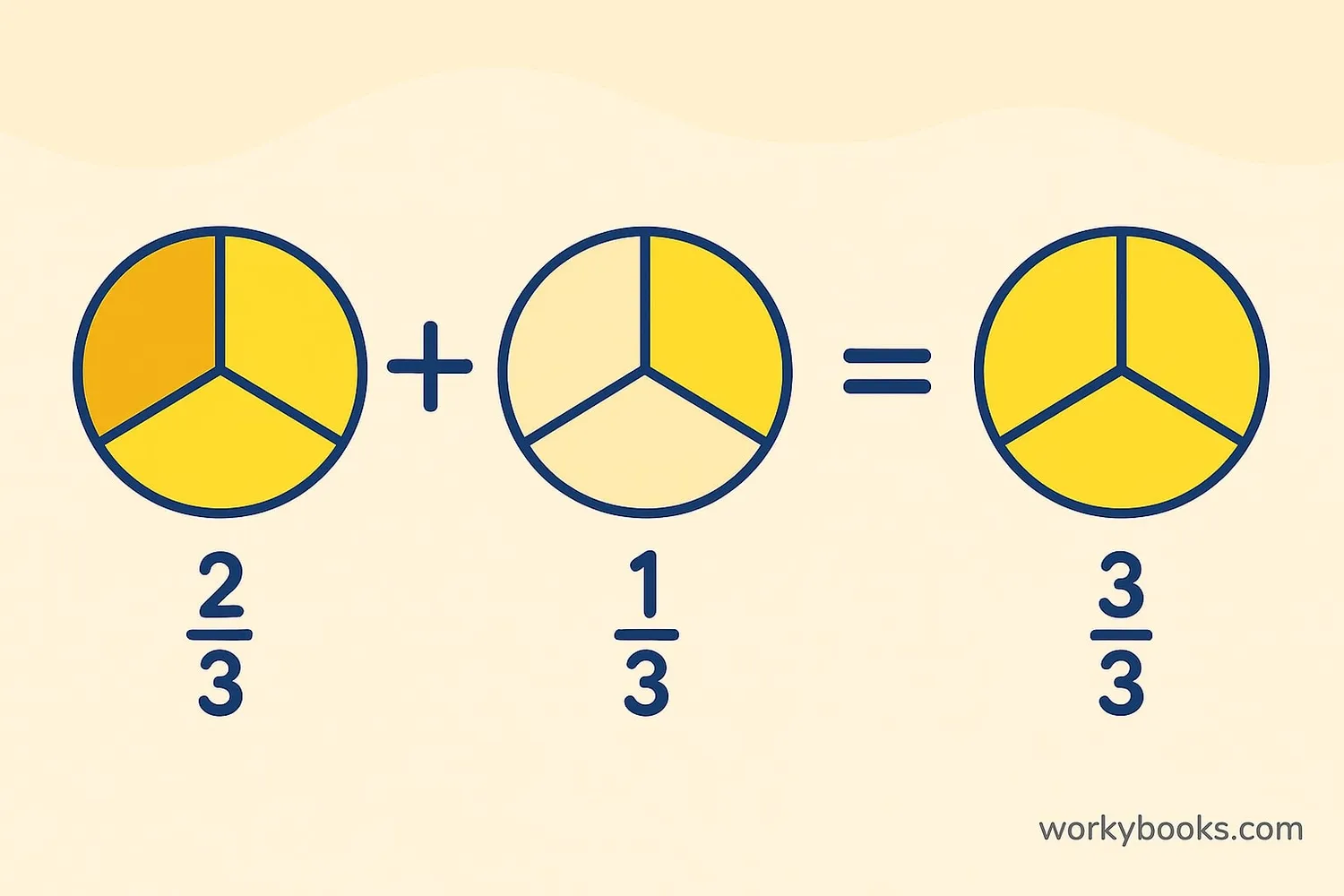
When fractions have the same denominator, adding them is simple! Just add the numerators and keep the same denominator.
Addition Formula
When denominators are the same, add the numerators and keep the denominator.
Step 1: Check denominators (both are 8) - they match!
Step 2: Add numerators: 3 + 2 = 5
Step 3: Keep the denominator: 8
Answer: ⁵⁄₈
This works because the fractions are describing parts of the same sized whole. Both are eighths, so we're just adding more eighths together.
Remember
Always check that the denominators are the same before adding numerators!
Adding Fractions with Different Denominators
When denominators are different, we can't add directly. We need to find a common denominator first.
Step 1: Find a common denominator (a number that both denominators divide into evenly)
Step 2: Convert both fractions to equivalent fractions with the common denominator
Step 3: Add the numerators and keep the common denominator
Step 4: Simplify the result if possible
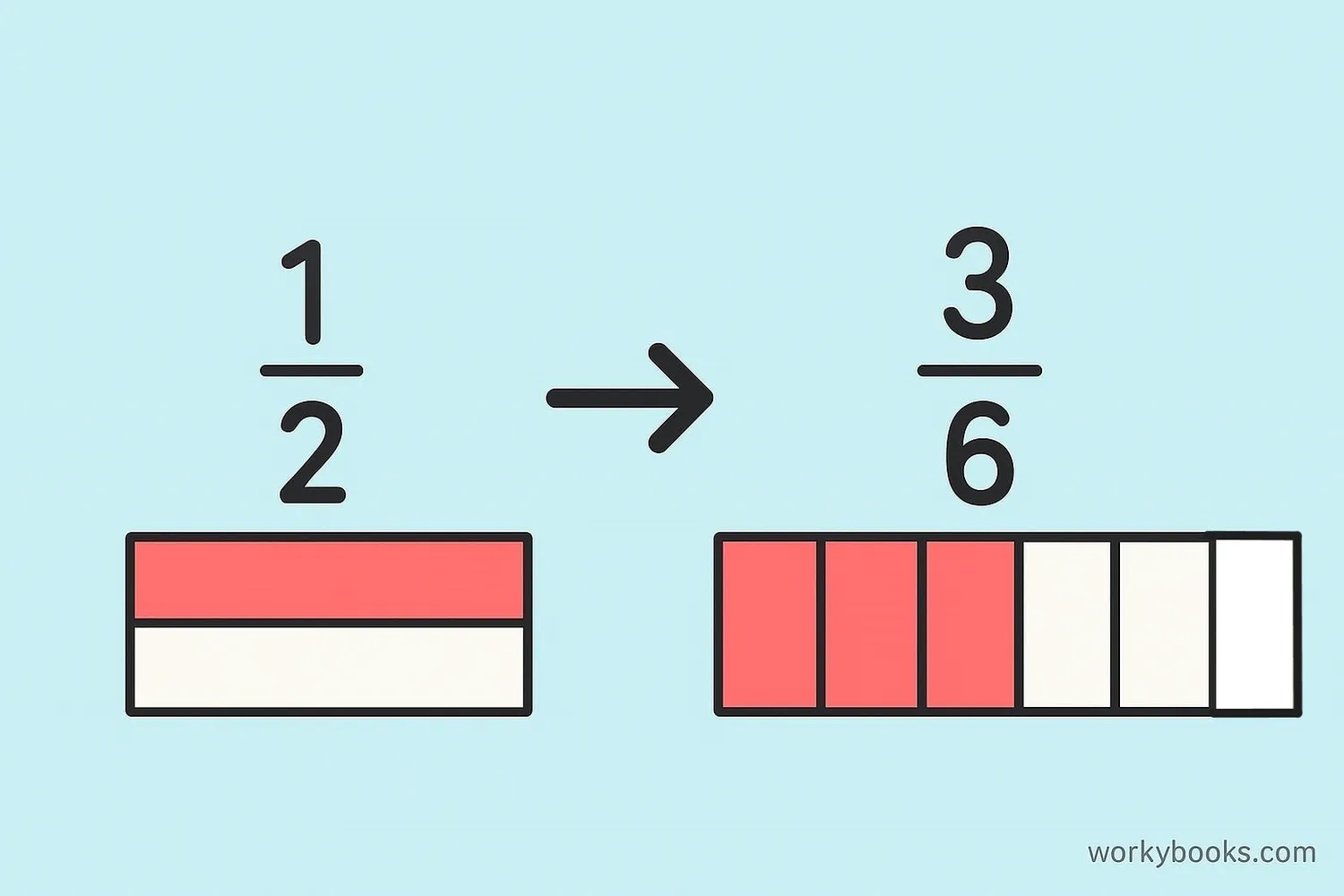
Example: Add ½ + ⅓
Step 1: Common denominator of 2 and 3 is 6
Step 2: Convert: ½ = ³⁄₆ and ⅓ = ²⁄₆
Step 3: Add: ³⁄₆ + ²⁄₆ = ⁵⁄₆
Step 4: ⁵⁄₆ is already simplified
Finding Common Denominators
To find a common denominator, look for the Least Common Multiple (LCM) of the denominators.
Conversion Tip
Multiply the denominators to quickly find a common denominator, but always look for the smallest one to make simplifying easier!
Adding Mixed Numbers
Mixed numbers combine whole numbers and fractions. To add them:
Method 1:
1. Add the whole numbers separately
2. Add the fractions
3. Combine the results
Example: 2¼ + 1½
Step 1: Add whole numbers: 2 + 1 = 3
Step 2: Add fractions: ¼ + ½ = ¼ + ²⁄₄ = ¾
Step 3: Combine: 3 + ¾ = 3¾
Method 2: Convert to improper fractions first
2¼ = ⁹⁄₄, 1½ = ³⁄₂ = ⁶⁄₄
⁹⁄₄ + ⁶⁄₄ = ¹⁵⁄₄ = 3¾
Remember
Always simplify your final answer and convert improper fractions to mixed numbers when needed!
Fraction Addition Practice Quiz
Test your fraction addition skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about adding fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They used unit fractions (fractions with 1 as numerator) and represented them with hieroglyphs.
Fractions in Nature
Fractions appear everywhere in nature! Flower petals often follow fractional patterns (like ⅓, ⅖, or ⅜ arrangements), and honeycomb cells form perfect hexagons that can be divided into fractional parts.
Fractions in Music
Musical rhythms are based on fractions. A whole note lasts 4 beats, a half note 2 beats, a quarter note 1 beat. Musicians add these fractions to create rhythms!
Fraction Records
The fraction with the largest denominator ever used in a published mathematical proof has a denominator of 10^46! But don't worry - you'll only need to work with much smaller fractions.


