Adding Integers - Definition, Examples, Quiz, FAQ, Trivia
Learn to add positive and negative numbers with easy explanations, visual examples, and practice activities
What are Integers?
Integers are whole numbers that can be positive, negative, or zero. They do not have fractions or decimals. Think of integers as steps on a staircase - you can go up (positive), down (negative), or stay on the same step (zero).
Positive integers are numbers greater than zero: 1, 2, 3, 4, ...
Negative integers are numbers less than zero: -1, -2, -3, -4, ...
Zero is neither positive nor negative: 0
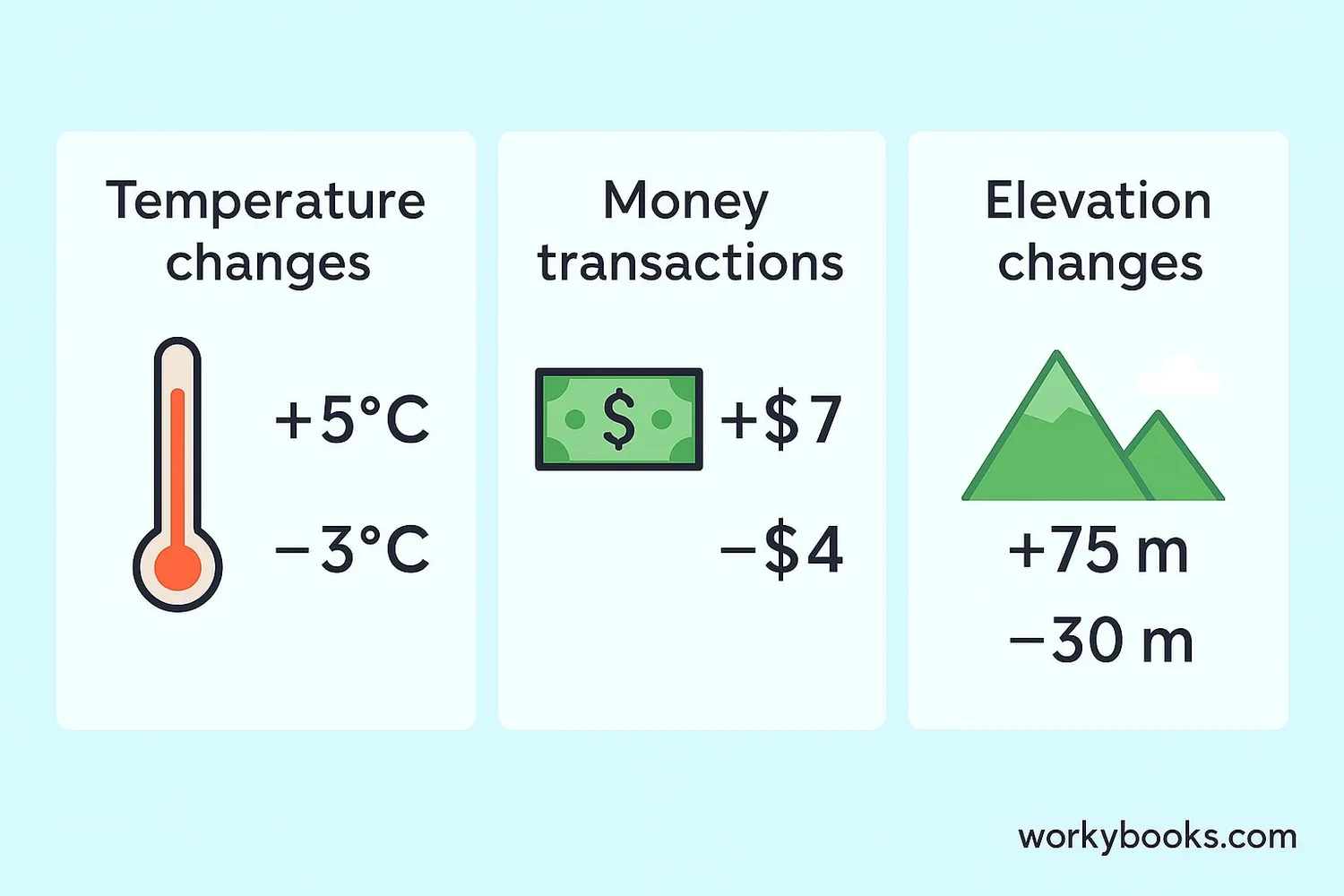
Integers are used in many real-life situations:
- Temperature: +25°C (warm) vs -5°C (cold)
- Elevation: 200m above sea level vs 50m below sea level
- Money: $10 earned vs $5 owed
Key Concept
Integers include all positive whole numbers, their negative counterparts, and zero. They do not include fractions or decimals.
Rules for Adding Integers

Adding integers follows three simple rules. Remembering these will help you solve any integer addition problem!
Same Signs
When both integers have the same sign (both positive or both negative), add their absolute values and keep the sign.
Different Signs
When integers have different signs, subtract the smaller absolute value from the larger one, and keep the sign of the number with the larger absolute value.
Adding Zero
When you add zero to any integer, the result is the integer itself.
Remember
The absolute value of a number is its distance from zero on the number line. For example, both +5 and -5 have an absolute value of 5.
Adding Integers on a Number Line
A number line is a visual tool that helps us understand integer addition. Here's how to use it:
Step 1: Draw a number line with zero in the center, positive numbers to the right, and negative numbers to the left.
Step 2: Start at the first number in your addition problem.
Step 3: Move in the direction of the second number's sign:
- Positive sign → move right
- Negative sign → move left
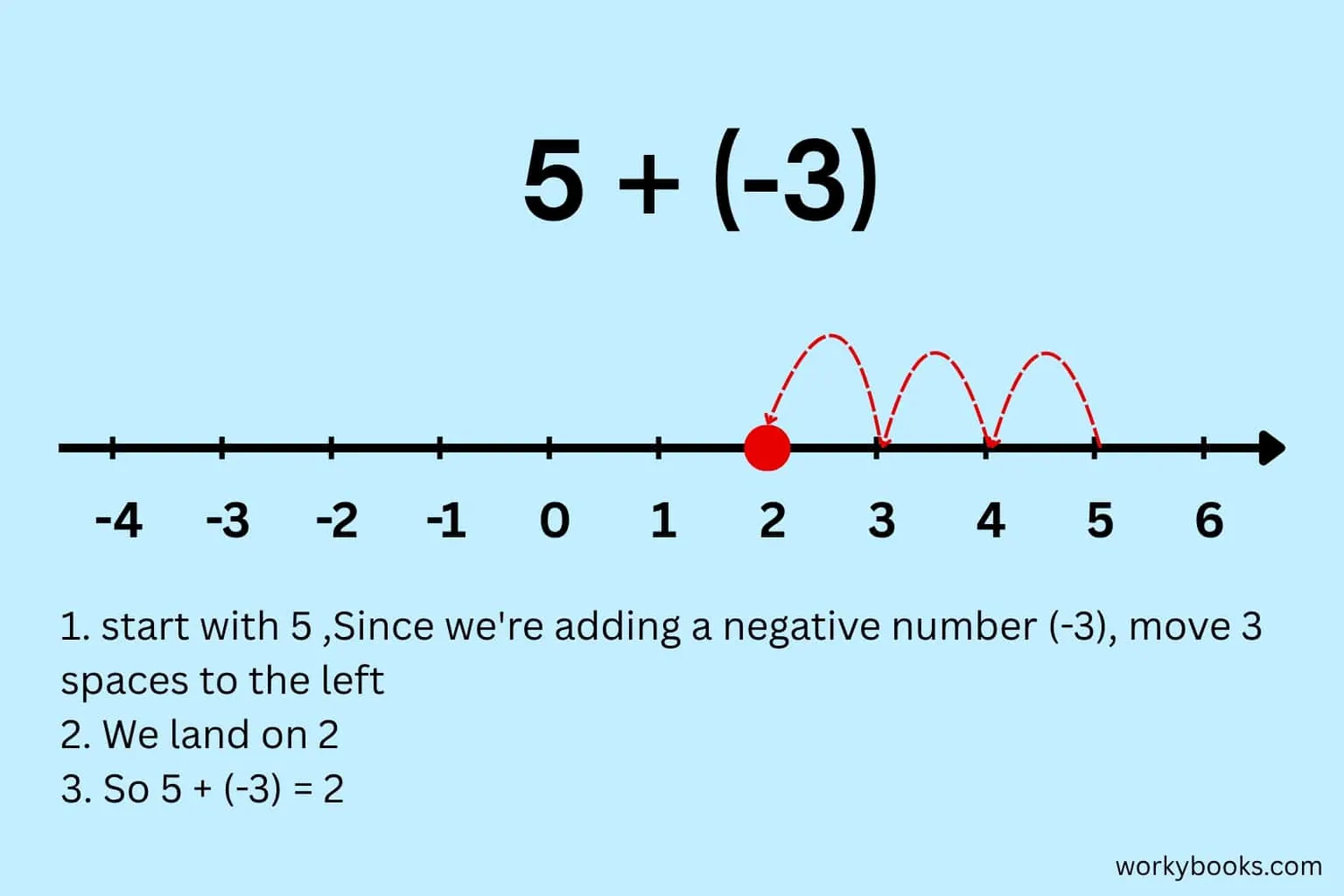
Example: Adding 5 + (-3)
1. Start at 5
2. Since we're adding a negative number (-3), move 3 spaces to the left
3. We land on 2
4. So 5 + (-3) = 2
Tip
Think of adding a positive as moving forward (right) and adding a negative as moving backward (left).
Solved Examples
Let's practice with some real-world examples:
Example 1: Temperature Change
The temperature was -5°C in the morning. By afternoon, it rose by 8°C. What is the new temperature?
Solution: Start at -5, add 8: -5 + 8 = 3°C
Example 2: Money Transactions
Sarah had $20. She spent $12 on a book, then earned $15 from her chores. What is her new balance?
Solution: 20 + (-12) + 15 = (20 - 12) + 15 = 8 + 15 = $23
Example 3: Elevation Change
A submarine was 120 meters below sea level. It rose 45 meters. What is its new position?
Solution: -120 + 45 = -75 meters (75 meters below sea level)
Example 4: Football Yardage
A football team gains 7 yards, then loses 10 yards, then gains 15 yards. What is their net yardage?
Solution: 7 + (-10) + 15 = (7 - 10) + 15 = -3 + 15 = +12 yards
Practice Tip
Look for integer addition in your daily life - temperature changes, money transactions, or video game scores!
Practice Quiz
Test your understanding of integer addition with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about adding integers:
Math Trivia
Discover interesting facts about integers and mathematics:
History of Negative Numbers
Negative numbers were first used in ancient China around 200 BCE. Mathematicians used red rods for positive numbers and black rods for negative numbers in their calculations.
Integers in Science
Integers are essential in physics for concepts like electric charge (positive protons, negative electrons) and direction (positive for forward, negative for backward).
Integers in Computing
Computers use integers for counting and calculations. The largest integer value in many programming languages is 2,147,483,647 because of how computers store numbers in 32 bits.
Integer Properties
Integers are closed under addition - meaning when you add any two integers, you always get another integer. This property makes them fundamental in mathematics.





