Adding Mixed Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn to add mixed numbers with easy explanations, visual examples, and practice activities
What are Mixed Numbers?
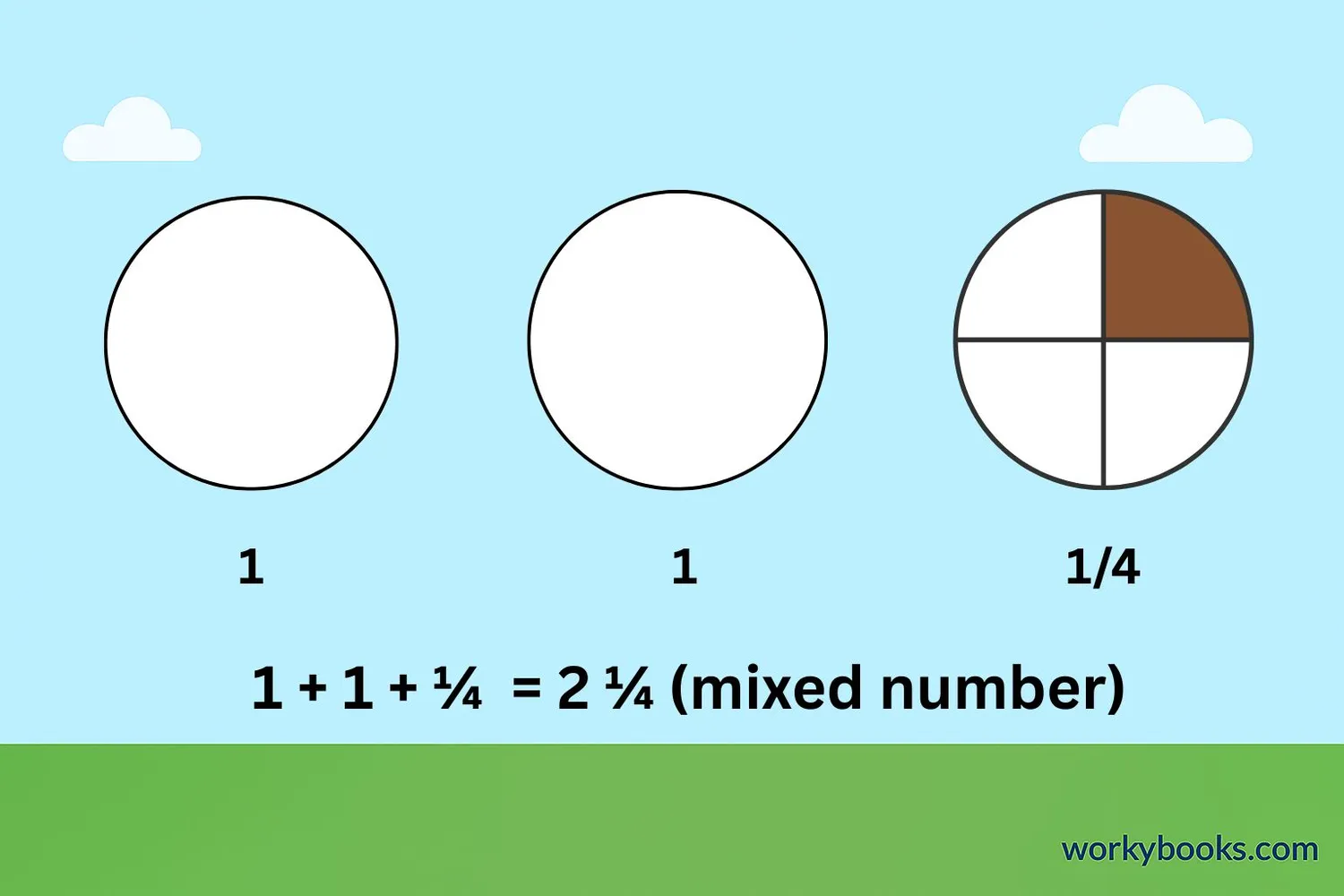
A mixed number combines a whole number and a fraction. For example, 2½ (two and a half) is a mixed number. The whole number is 2 and the fraction is ½.
Mixed numbers are useful when we have more than one whole thing plus part of another. For example, if you have 2 whole pizzas and half of another pizza, you have 2½ pizzas.
When we add mixed numbers, we add the whole numbers and the fractions separately. Sometimes we need to convert the fractions to have common denominators before adding.
Key Concept
A mixed number = whole number + fraction. To add mixed numbers, add the whole numbers and fractions separately.
Adding with Like Denominators

When mixed numbers have fractions with the same denominator, adding is straightforward:
Add just the whole number parts together
Add just the fraction parts together
If the fraction is improper (numerator larger than denominator), convert it to a mixed number and add it to your whole number
Example: 2¾ + 1¼
Remember
Always simplify your fraction after adding. If the fraction is improper, convert it to a mixed number and add it to your whole number.
Adding with Unlike Denominators

When the denominators are different, we need to find a common denominator before we can add the fractions:
Find the least common multiple (LCM) of the denominators
Change both fractions to equivalent fractions with the common denominator
Add the whole numbers together
Add the fractions together
Simplify the fraction and convert to a mixed number if needed
Example: 1½ + 2⅓
Conversion Tip
Always find the smallest common denominator to make your fractions easier to work with.
Practice Examples

Example 1: Like Denominators
Solve: 3⅔ + 2⅓
Example 2: Unlike Denominators
Solve: 4¾ + 2⅔
Example 3: Real-World Problem
Maria walked 1⅖ miles to school and 2⅗ miles to her friend's house. How far did she walk in total?
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about adding mixed numbers:
Fractions Trivia
Discover interesting facts about fractions and mixed numbers:
Ancient Fractions
The ancient Egyptians used fractions over 4,000 years ago. They had special symbols for common fractions like ½, ⅓, and ¼, but represented other fractions as sums of unit fractions.
Fraction Origins
The word "fraction" comes from the Latin word "fractio" which means "to break." This makes sense because fractions break whole numbers into smaller parts.
Fractions in Nature
Fractions appear everywhere in nature! From the spirals in seashells (Fibonacci sequence) to the segments in orange slices, fractions help us describe patterns in the natural world.
Largest Fraction
The largest possible fraction with a numerator and denominator is when the denominator is 1 and the numerator is the largest number you can imagine. But as a mixed number, it would be that whole number!


