Addition and Subtraction of Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn to work with fractions through easy explanations, visual examples, and practice activities
Understanding Fractions
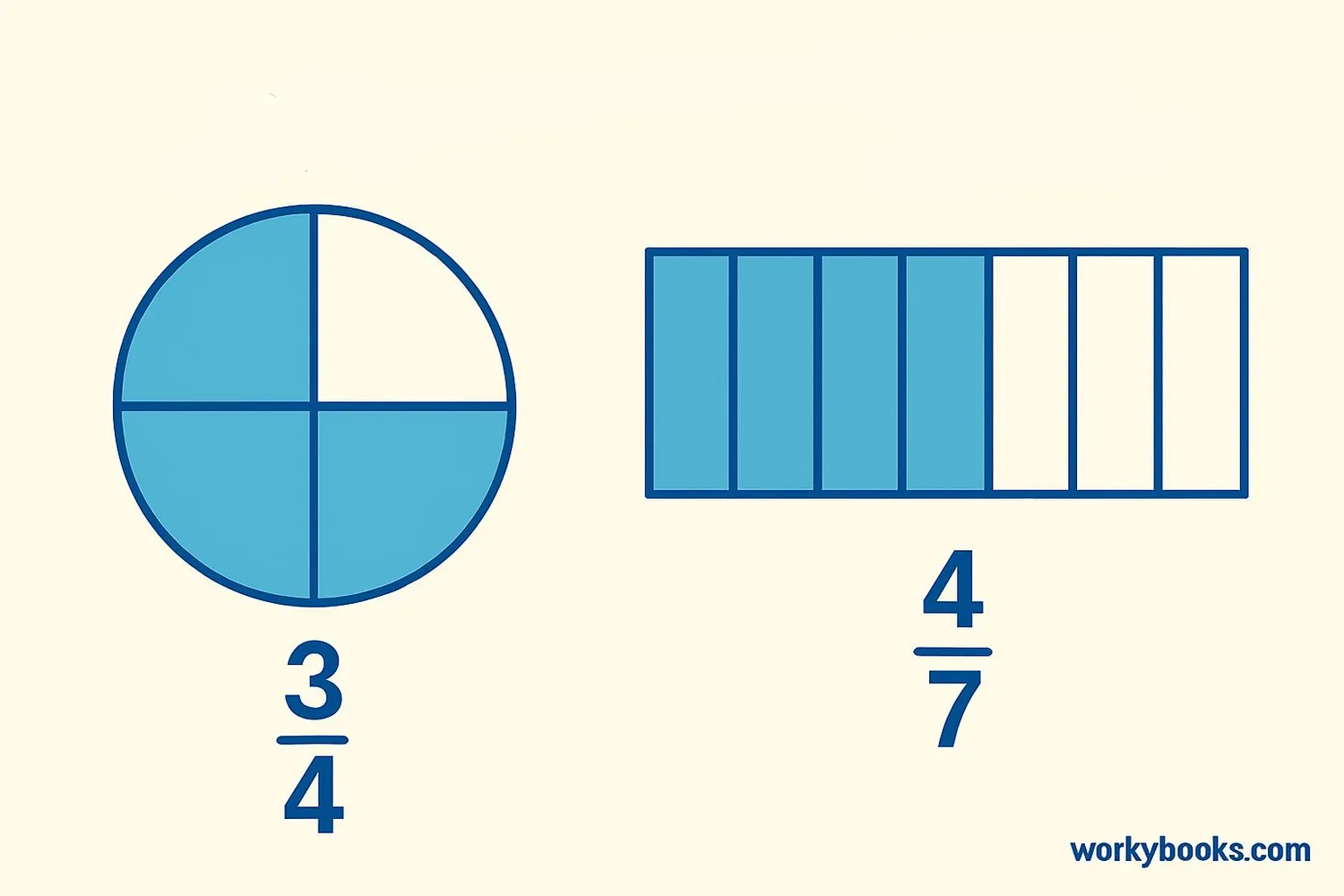
A fraction represents parts of a whole. The top number is called the numerator and tells us how many parts we have. The bottom number is the denominator and tells us how many equal parts the whole is divided into.
For example, in the fraction ¾, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts.
Fractions are used everywhere - when sharing food, measuring ingredients, telling time, and in many math problems. Understanding fractions helps us describe parts of things accurately.
Key Concept
The denominator tells us how many parts make a whole. The numerator tells us how many of those parts we have.
Adding and Subtracting Like Fractions
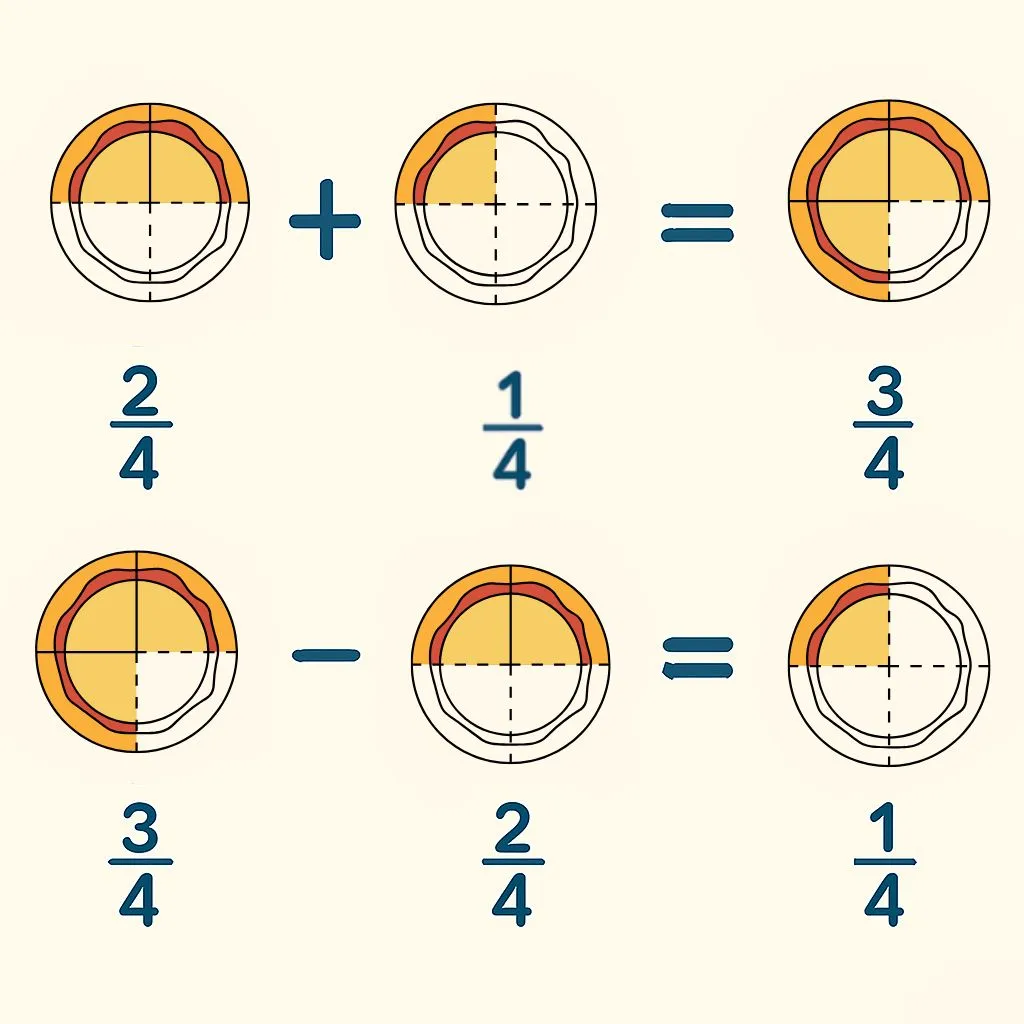
Like fractions have the same denominator. Adding and subtracting them is simple because the denominator stays the same. We only add or subtract the numerators.
Addition Example:
Since the denominators are the same (5), we just add the numerators: 1 + 2 = 3. The denominator stays 5.
Subtraction Example:
Since the denominators are the same (8), we just subtract the numerators: 5 - 3 = 2. The denominator stays 8. Remember to simplify if possible - 2/8 simplifies to 1/4.
Remember
When adding or subtracting like fractions, only the numerators change. The denominator stays the same.
Adding and Subtracting Unlike Fractions
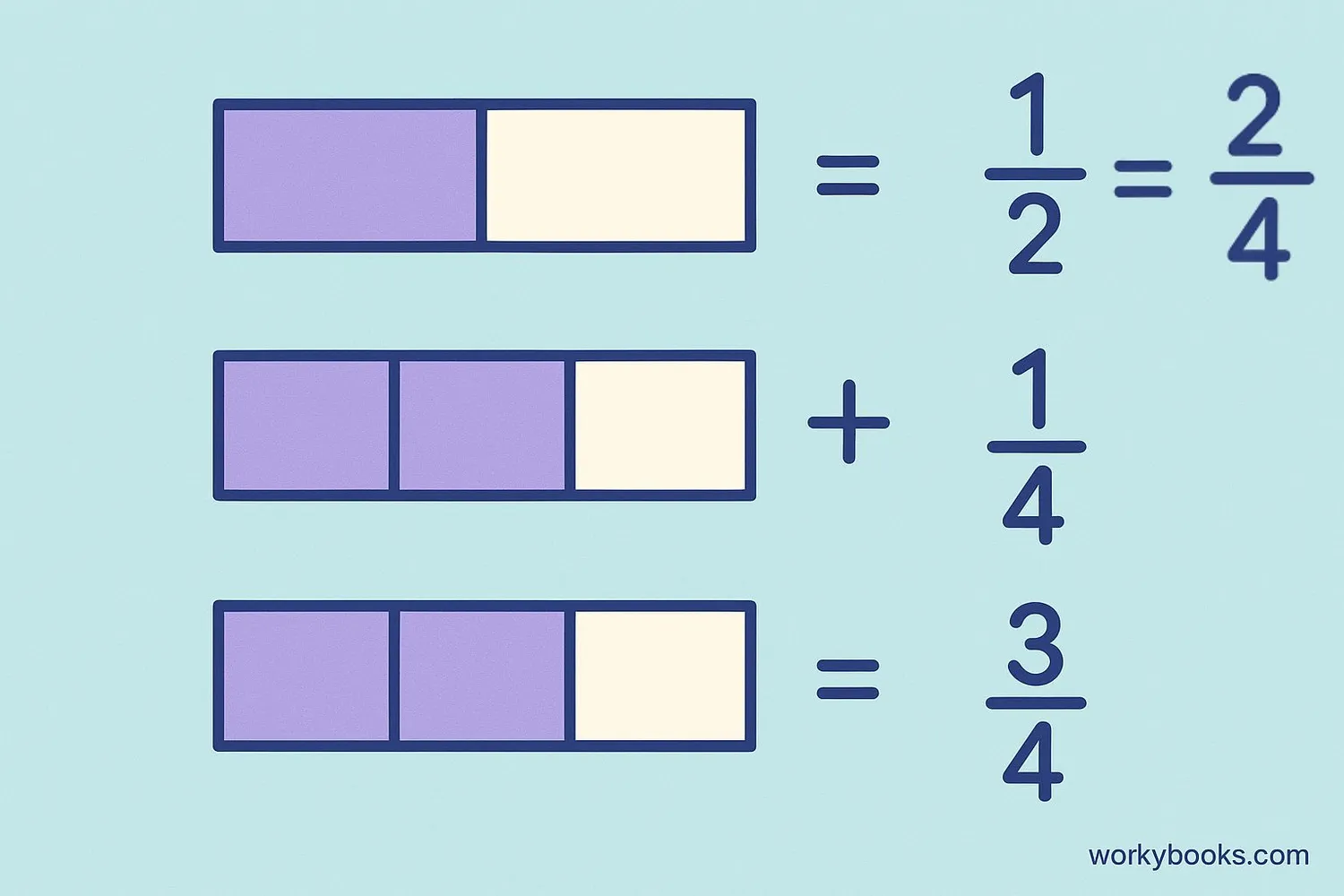
Unlike fractions have different denominators. To add or subtract them, we first need to find a common denominator. The common denominator is a number that both denominators can divide into evenly.
Step-by-Step Addition:
1. Find a common denominator (often the Least Common Multiple of the denominators)
2. Convert both fractions to equivalent fractions with that denominator
3. Add the numerators
4. Simplify the resulting fraction if possible
Example: ½ + ⅓
Step 1: Common denominator of 2 and 3 is 6
Step 2: ½ = 3/6 and ⅓ = 2/6
Step 3: 3/6 + 2/6 = 5/6
Step-by-Step Subtraction:
1. Find a common denominator
2. Convert both fractions
3. Subtract the numerators
4. Simplify if possible
Example: ¾ - ⅙
Step 1: Common denominator of 4 and 6 is 12
Step 2: ¾ = 9/12 and ⅙ = 2/12
Step 3: 9/12 - 2/12 = 7/12
Conversion Tip
The Least Common Denominator (LCD) is the smallest number that is a common multiple of both denominators.
Adding and Subtracting Mixed Numbers
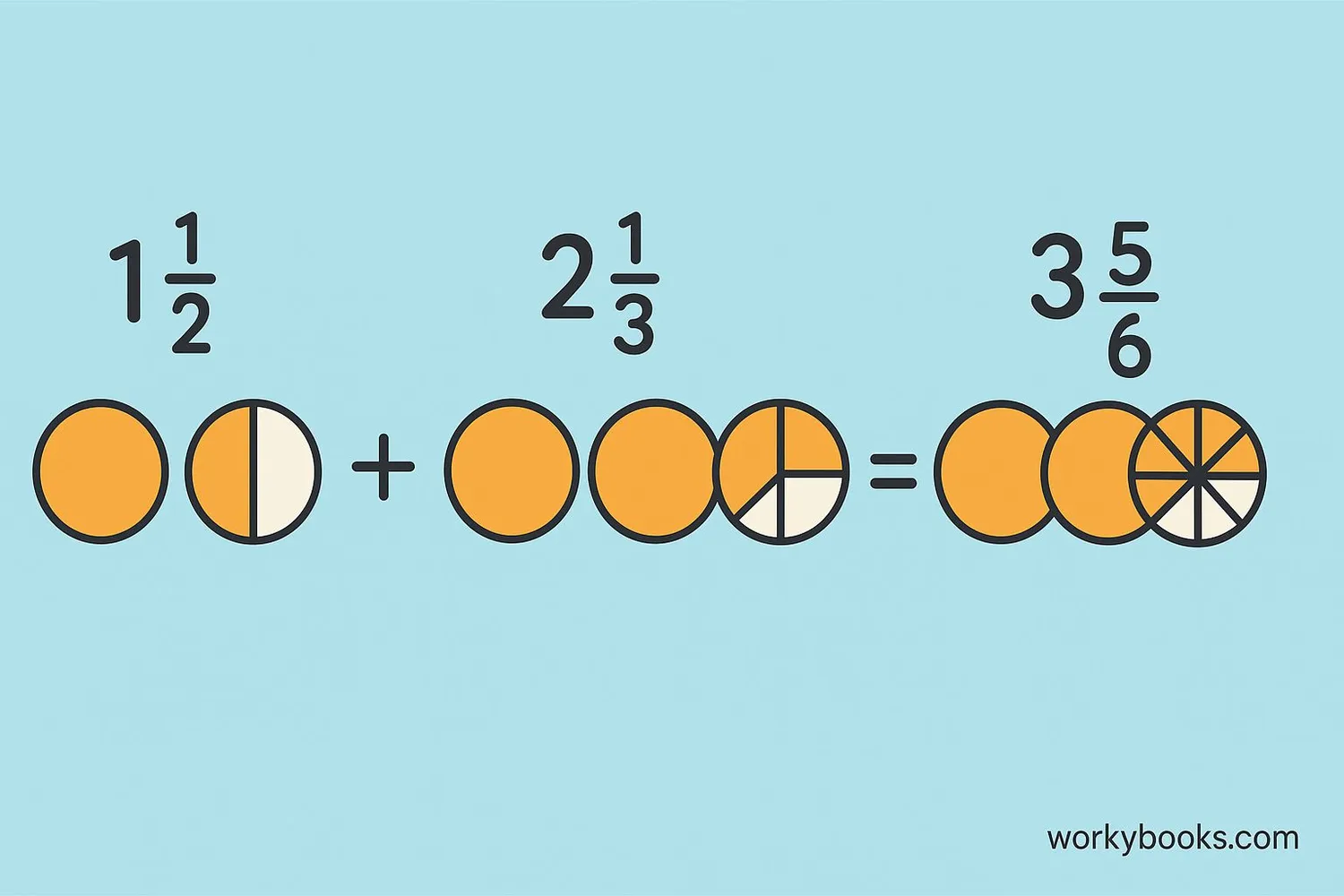
Mixed numbers combine a whole number with a fraction (like 2½). To add or subtract mixed numbers:
Method 1:
1. Add/subtract the whole numbers separately
2. Add/subtract the fractions
3. Combine the results
Example: 2½ + 1¼
Step 1: Whole numbers: 2 + 1 = 3
Step 2: Fractions: ½ + ¼ = ¾
Step 3: Combine: 3 + ¾ = 3¾
Method 2:
1. Convert mixed numbers to improper fractions
2. Add/subtract the improper fractions
3. Convert back to mixed numbers
Example: 2½ - 1⅓
Step 1: 2½ = 5/2, 1⅓ = 4/3
Step 2: Common denominator of 2 and 3 is 6
5/2 = 15/6, 4/3 = 8/6
15/6 - 8/6 = 7/6
Step 3: 7/6 = 1⅙
Both methods work, but Method 1 is often easier when fractions have common denominators, while Method 2 is useful when denominators are different.
Remember
When subtracting mixed numbers, you might need to borrow from the whole number if the fraction being subtracted is larger.
Fractions Practice Quiz
Test your fraction skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about adding and subtracting fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They had special symbols for fractions with 1 in the numerator, like 1/2, 1/3, and 1/4. These were called unit fractions.
Fractions in Nature
Fractions appear throughout nature. The patterns in flower petals, leaves on stems, and even the spirals in pinecones and sunflowers follow the Fibonacci sequence, which creates fractions.
Fractions in Music
Musical notes represent fractions of time. A whole note lasts four beats, a half note lasts two beats, a quarter note lasts one beat, and so on. Rhythm is essentially fractions in action!
Fraction Records
The fraction with the largest denominator ever used in a mathematical proof is 1/2,217,421,013. Mathematicians sometimes work with incredibly small fractions!


