Adjacent Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn about angle relationships with easy explanations, visual examples, and practice activities
What are Adjacent Angles?
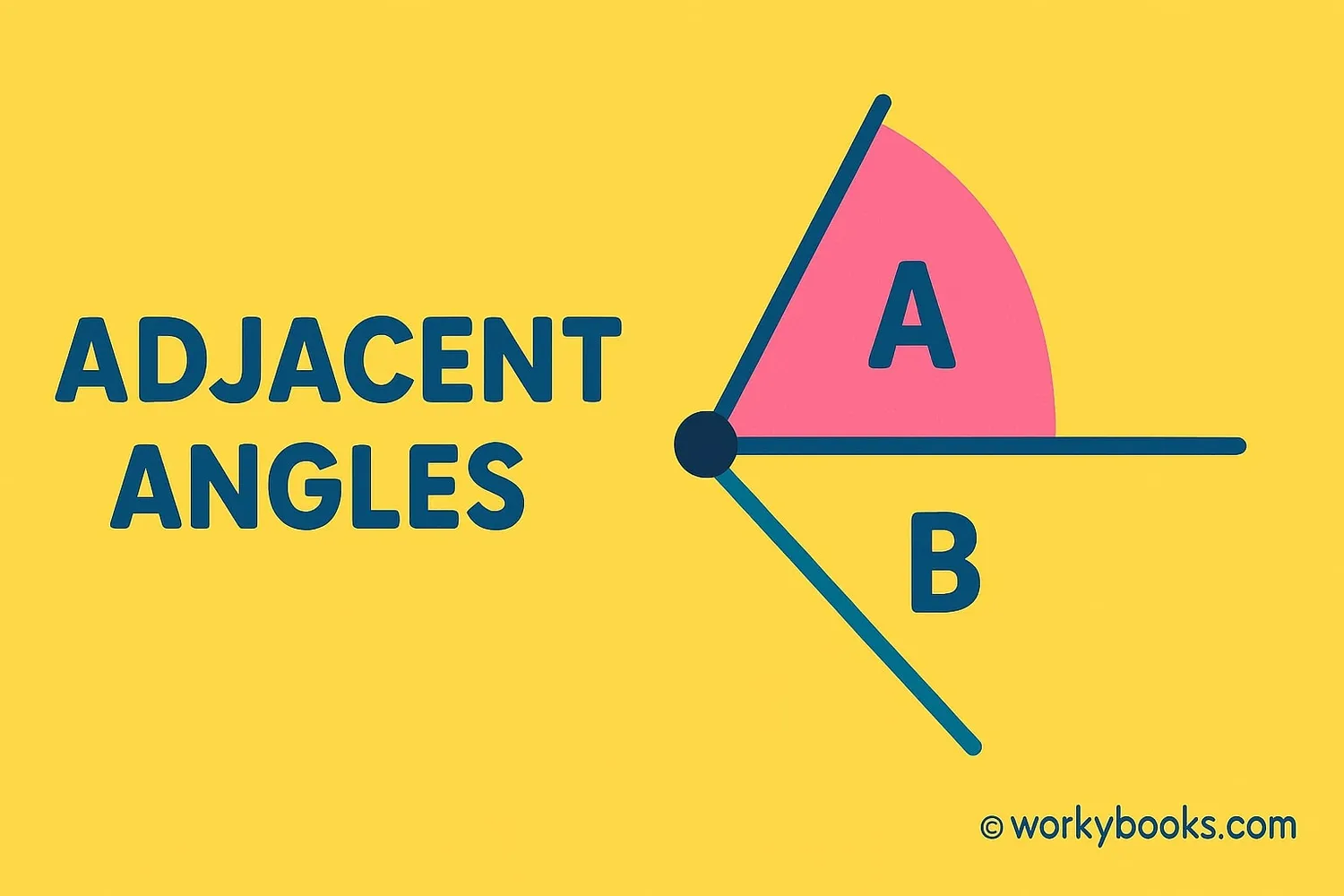
Adjacent angles are two angles that are next to each other and share two important things:
1. A common vertex (the corner point where angles meet)
2. A common side (the ray between them)
Adjacent angles don't overlap and are side-by-side. They can be any size - big or small - as long as they share the same vertex and one side.
Think of adjacent angles like neighbors who share a fence. Each neighbor has their own yard (angle), but they share the fence line (common side) and the corner post (common vertex).
Key Concept
Adjacent angles must share both a common vertex and a common side. If angles share only a vertex but not a side, they are vertical angles, not adjacent.
Properties of Adjacent Angles
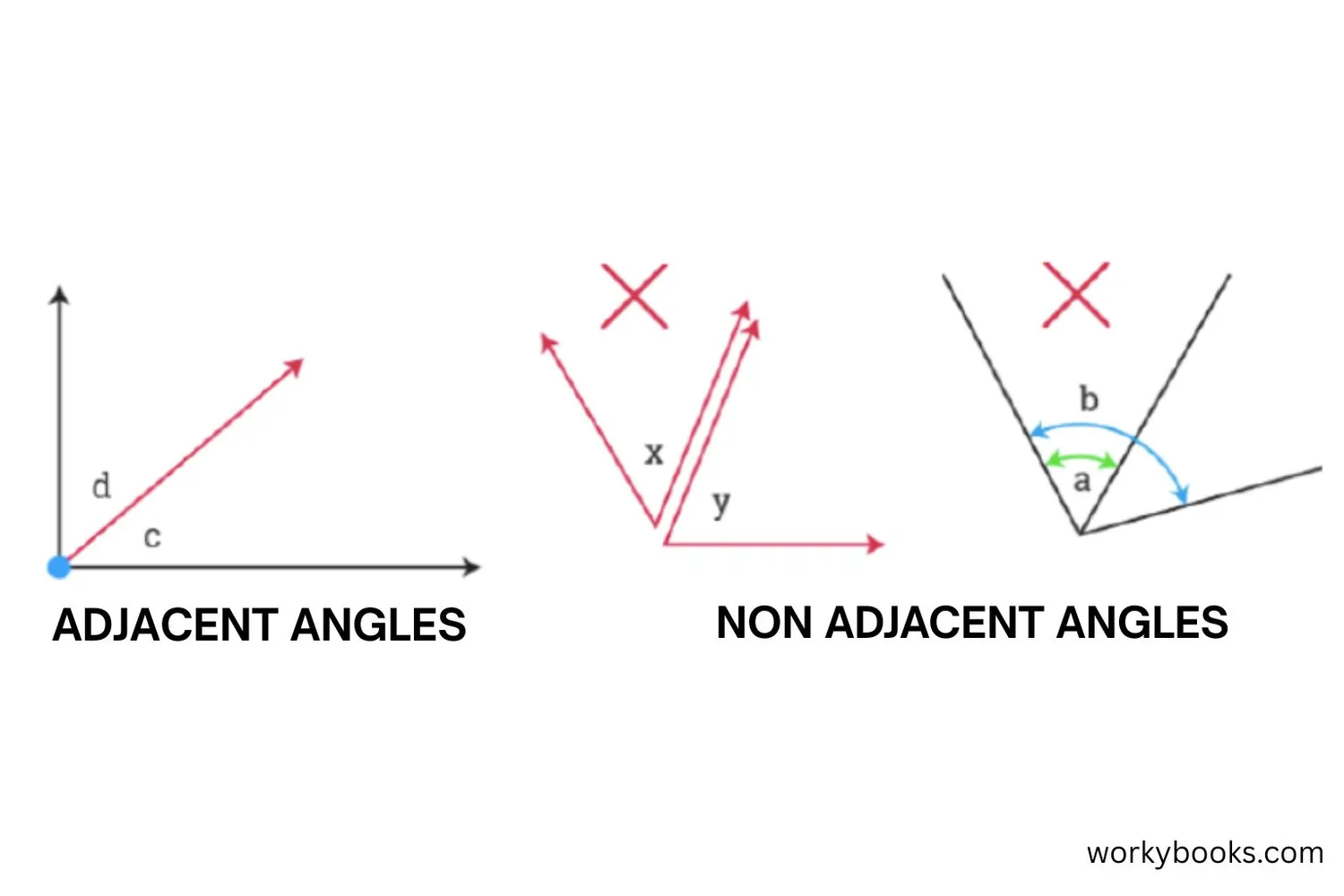
Adjacent angles have special properties that help us identify them:
1. Common Vertex: Both angles must share the same corner point.
2. Common Side: The angles must share one side between them.
3. No Overlap: The angles do not overlap each other.
4. Side-by-Side: They are positioned next to each other.
5. Same Plane: Both angles lie on the same flat surface.
Adjacent angles can be any size, but when they form a straight line together, they have special properties. These are called a linear pair and they always add up to 180°.
Remember
Adjacent angles don't have to be equal. They can be different sizes as long as they share a vertex and a side without overlapping.
Adjacent Angles and Other Angle Relationships
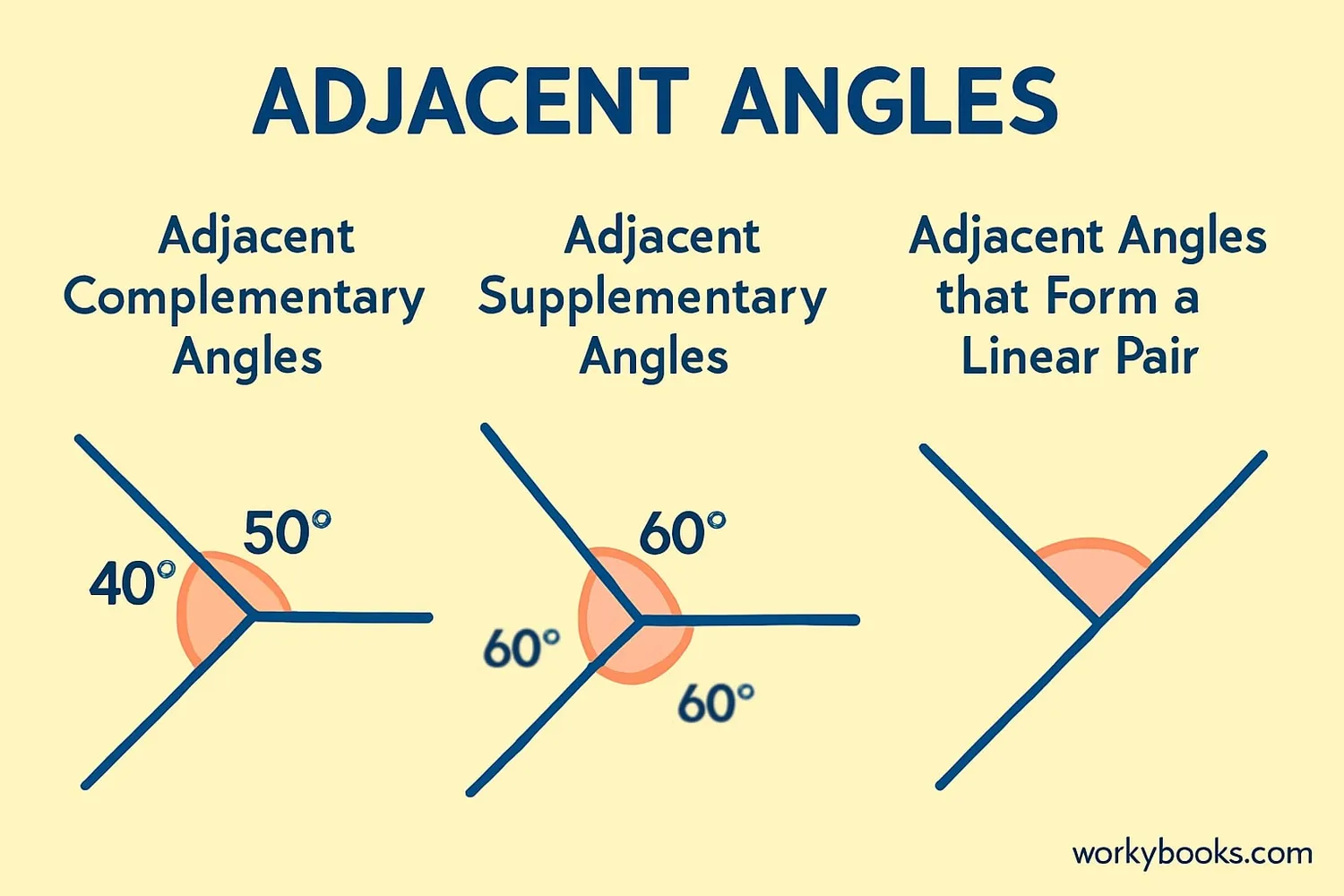
Adjacent angles can have special relationships with each other:
Complementary Adjacent Angles: When two adjacent angles add up to 90°. For example, 30° and 60° angles that share a common vertex and side.
Supplementary Adjacent Angles: When two adjacent angles add up to 180°. These are also called a linear pair. For example, 120° and 60° angles that form a straight line together.
Adjacent angles are different from:
Vertical Angles: Angles opposite each other when two lines cross. They share a vertex but not a side.
Alternate Angles: Angles on opposite sides of a transversal line.
In a parallelogram, consecutive angles are adjacent and supplementary - they always add up to 180°.
Important Note
Not all adjacent angles are complementary or supplementary. They can have any measures as long as they share a vertex and side.
Real-World Examples

Adjacent angles appear all around us in everyday objects:
Example 1: Scissors
When you open scissors, the angles formed between the blades and the handle are adjacent angles. They share a common vertex at the screw that holds the blades together.
Example 2: Clock
The hands of a clock form adjacent angles with the center of the clock as their common vertex. The angle between the hour and minute hands changes as time passes.
Example 3: Book
When you open a book, the angles formed at the spine are adjacent angles. Each page forms adjacent angles with the spine as the common side.
Example 4: Ladder
A ladder leaning against a wall forms adjacent angles with the ground and the wall. The angle between the ladder and the ground and the angle between the ladder and the wall are adjacent angles sharing the point where the ladder touches the ground.
Real-World Tip
Look for corners and joints in objects - these are often vertices where adjacent angles form.
Adjacent Angles Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about adjacent angles:
Geometry Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Measurement
The Babylonians first divided circles into 360 degrees around 1800 BCE. They chose 360 because it has many divisors and matched their base-60 number system.
Nature's Angles
Honeybees build their honeycombs with perfect hexagonal cells. The adjacent angles in these hexagons are always 120°, creating the most efficient shape for storing honey.
Architecture Angles
The Great Pyramid of Giza in Egypt has sides that slope at an angle of about 51.8°. This angle was chosen because it creates a pyramid with height and base measurements in the golden ratio.
Right Angle Dominance
In a survey of all man-made structures, right angles (90°) are the most common angle by far. This is because right angles create stable, efficient structures and are easier to measure and construct.





