Alternate Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn about alternate interior and exterior angles with visual examples and practice activities
What Are Alternate Angles?
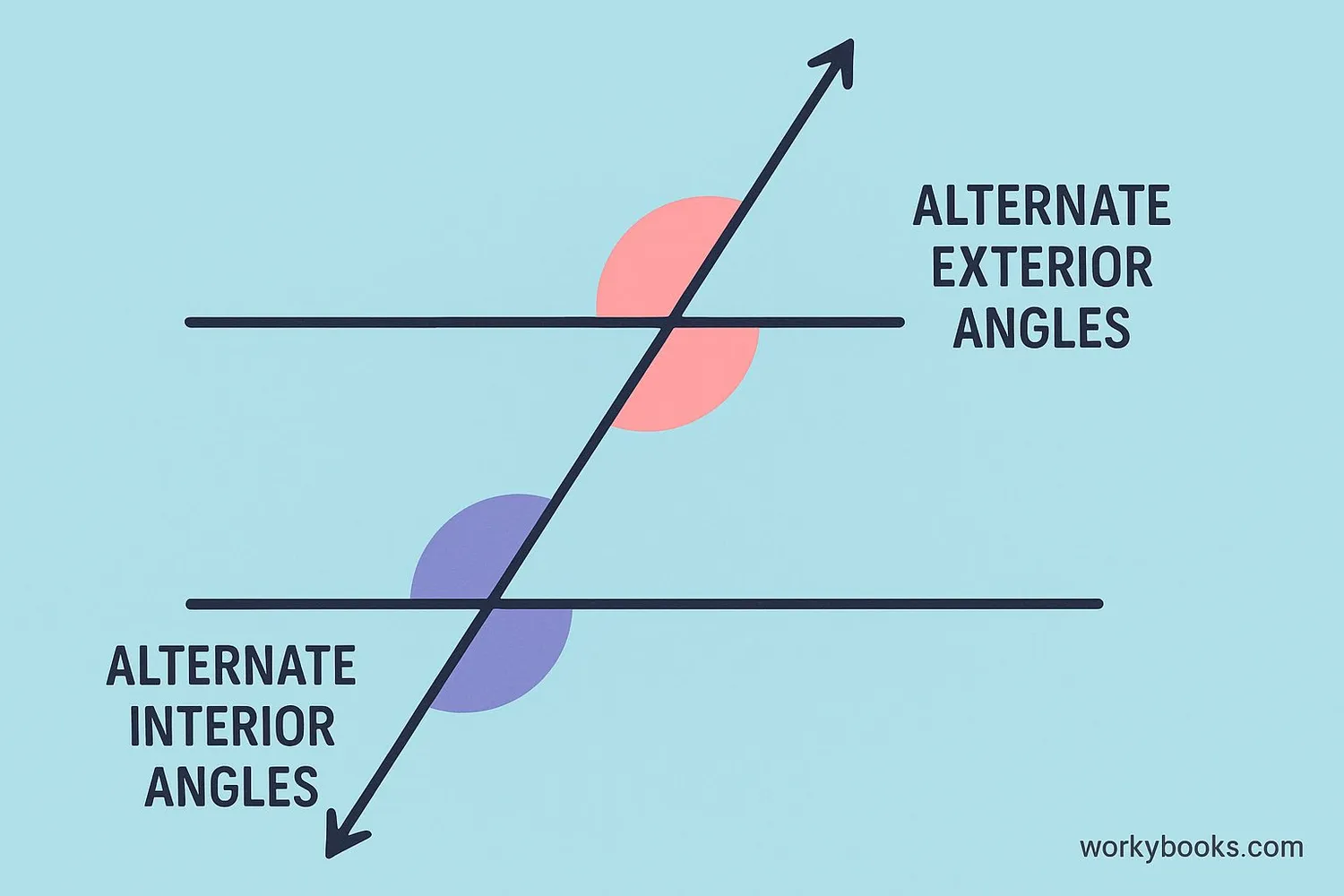
Alternate angles are special pairs of angles formed when two parallel lines are crossed by another line called a transversal. These angles are found on opposite sides of the transversal and have equal measurements.
When two parallel lines are cut by a transversal:
- Eight angles are created
- Four interior angles are between the parallel lines
- Four exterior angles are outside the parallel lines
- Alternate angles are pairs that are equal in measure
Key Concept
Alternate angles are always equal when formed by parallel lines and a transversal. They create a "Z" shape pattern.
Types of Alternate Angles
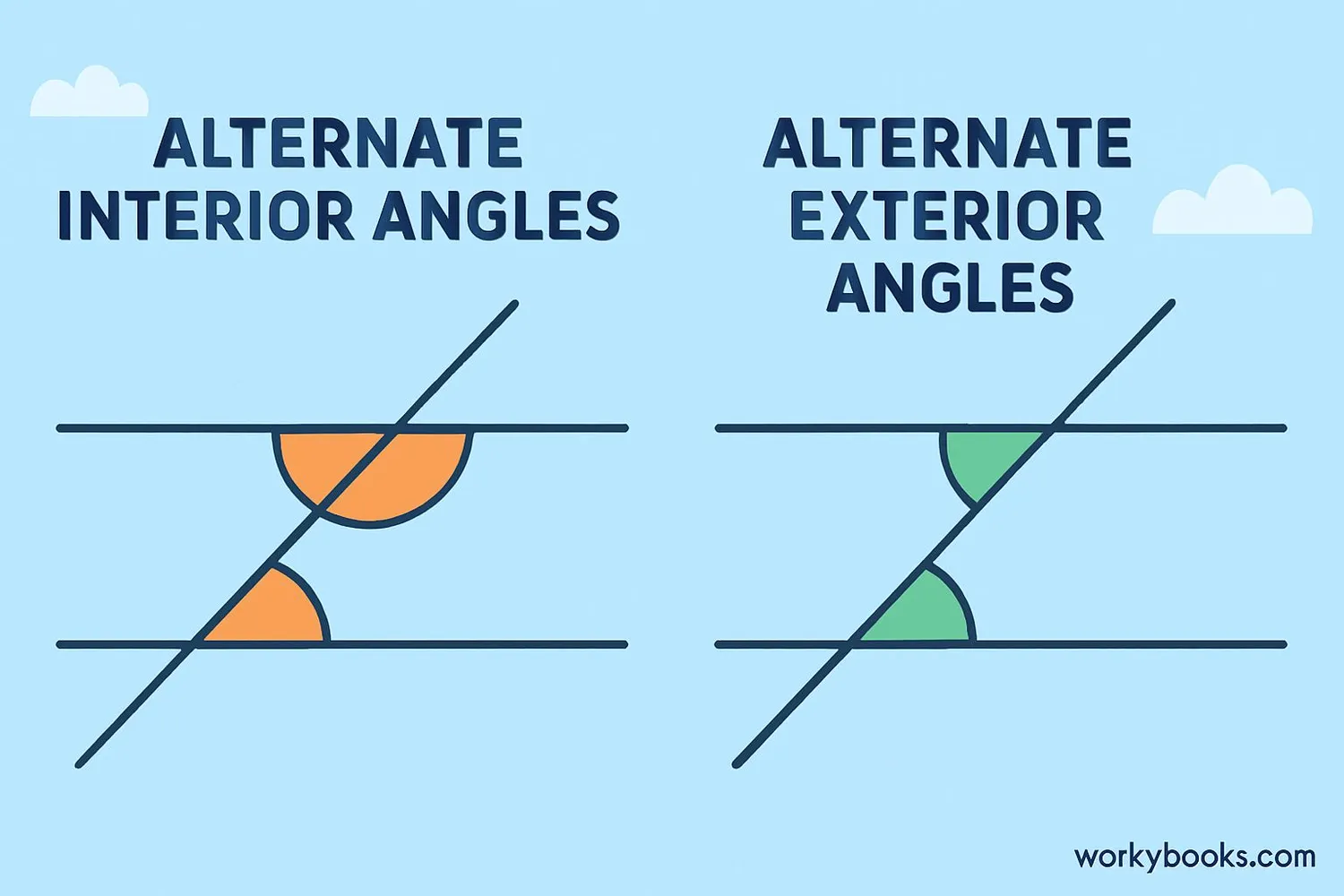
There are two main types of alternate angles:
1. Alternate Interior Angles
These angles are inside the parallel lines and on opposite sides of the transversal. They form a "Z" shape.
∠4 and ∠5
2. Alternate Exterior Angles
These angles are outside the parallel lines and on opposite sides of the transversal. They form a backwards "Z" shape.
∠2 and ∠7
Remember
Alternate angles are only equal when the lines are parallel. If the lines aren't parallel, the angles won't be equal.
Theorems and Properties
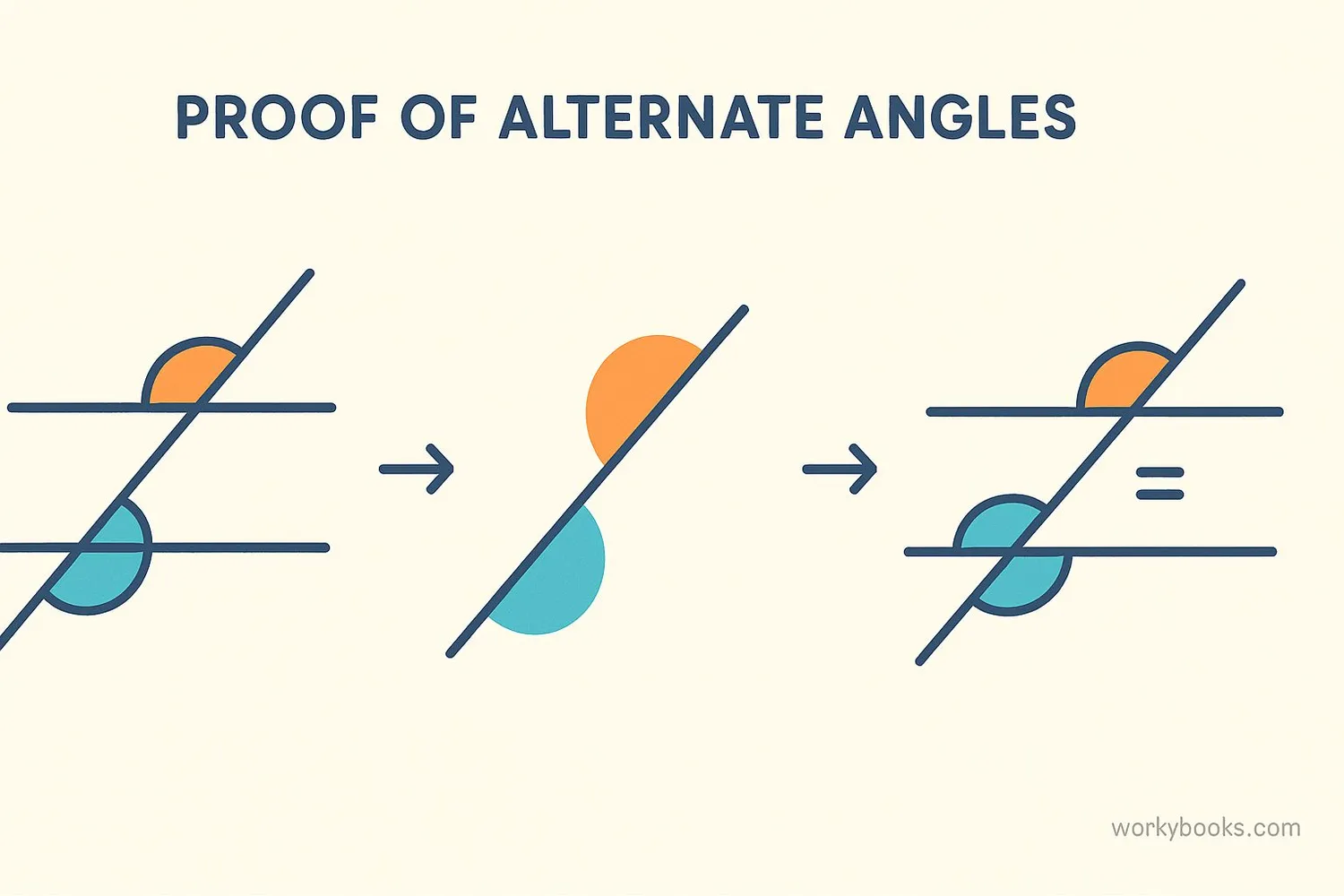
The properties of alternate angles are described by two important theorems:
Alternate Interior Angles Theorem: If two parallel lines are cut by a transversal, then the alternate interior angles are congruent (equal).
Alternate Exterior Angles Theorem: If two parallel lines are cut by a transversal, then the alternate exterior angles are congruent (equal).
These theorems help us solve for unknown angles in geometric figures. Here are some key properties:
| Angle Type | Position | Relationship |
|---|---|---|
| Alternate Interior | Inside parallel lines | Equal |
| Alternate Exterior | Outside parallel lines | Equal |
| Corresponding | Same relative position | Equal |
| Consecutive Interior | Same side of transversal | Supplementary (add to 180°) |
| Vertical Angles | Opposite each other | Equal |
Memory Tip
Remember "Alternate angles make Z's!" - the shape of alternate angles resembles the letter Z.
Real-World Examples
Let's solve some examples using alternate angles:
Example 1: In the diagram, lines l and m are parallel. If ∠3 = 65°, what is ∠6?
Solution: Since ∠3 and ∠6 are alternate interior angles, ∠6 = 65°.
Example 2: Lines a and b are parallel. If ∠1 = 110°, what is ∠8?
Solution: ∠1 and ∠8 are alternate exterior angles, so ∠8 = 110°.
Example 3: Find the measure of angle x in the diagram:
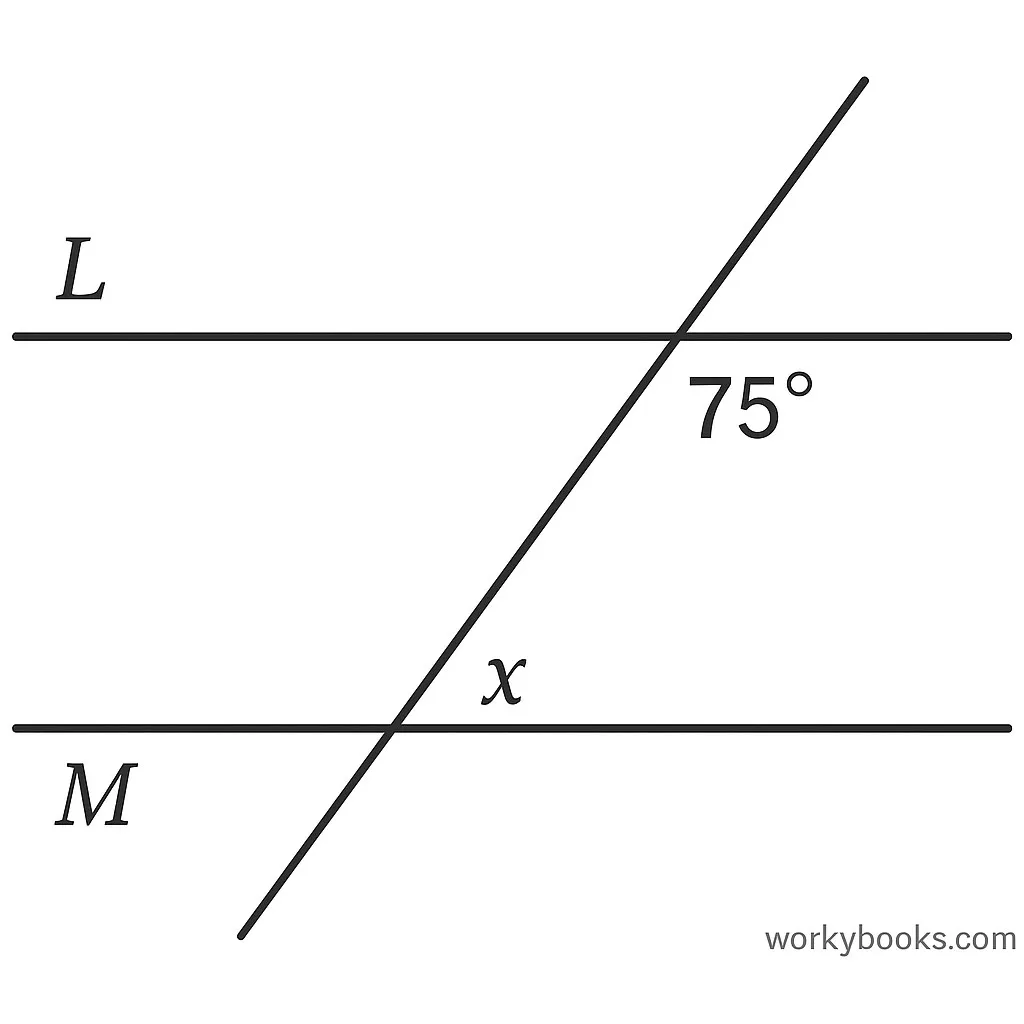
Solution: Since the lines are parallel, the alternate interior angles are equal. Therefore, x = 75°.
Example 4: In a building design, two parallel beams are crossed by a support beam. If one interior angle is 45°, what is the alternate interior angle?
Solution: Alternate interior angles are equal, so the other angle is also 45°.
Application Tip
Architects and engineers use alternate angle properties when designing structures with parallel elements like bridges and buildings.
Alternate Angles Quiz
Test your understanding of alternate angles with this 5-question quiz:
Frequently Asked Questions
Common questions about alternate angles:
Geometry Trivia
Fascinating facts about angles and geometry:
Ancient Angle Masters
The ancient Egyptians used angle properties to build the pyramids over 4,500 years ago. Their understanding of geometry was remarkably advanced for the time.
Nature's Geometry
Honeybees build honeycombs with perfect hexagonal shapes that demonstrate angle relationships. These hexagons use 120° angles, which are formed by alternate angle principles.
Art and Angles
Renaissance artists like Leonardo da Vinci used angle properties to create perspective in their paintings. This technique made flat images appear three-dimensional.
Angle Measurement
The concept of measuring angles in degrees dates back to ancient Babylonians around 3,000 years ago. They used a base-60 number system which is why circles have 360 degrees (6 × 60).




