Angle Bisector - Definition, Examples, Quiz, FAQ, Trivia
Learn to divide angles equally with step-by-step constructions, examples, and practice activities
What is an Angle Bisector?
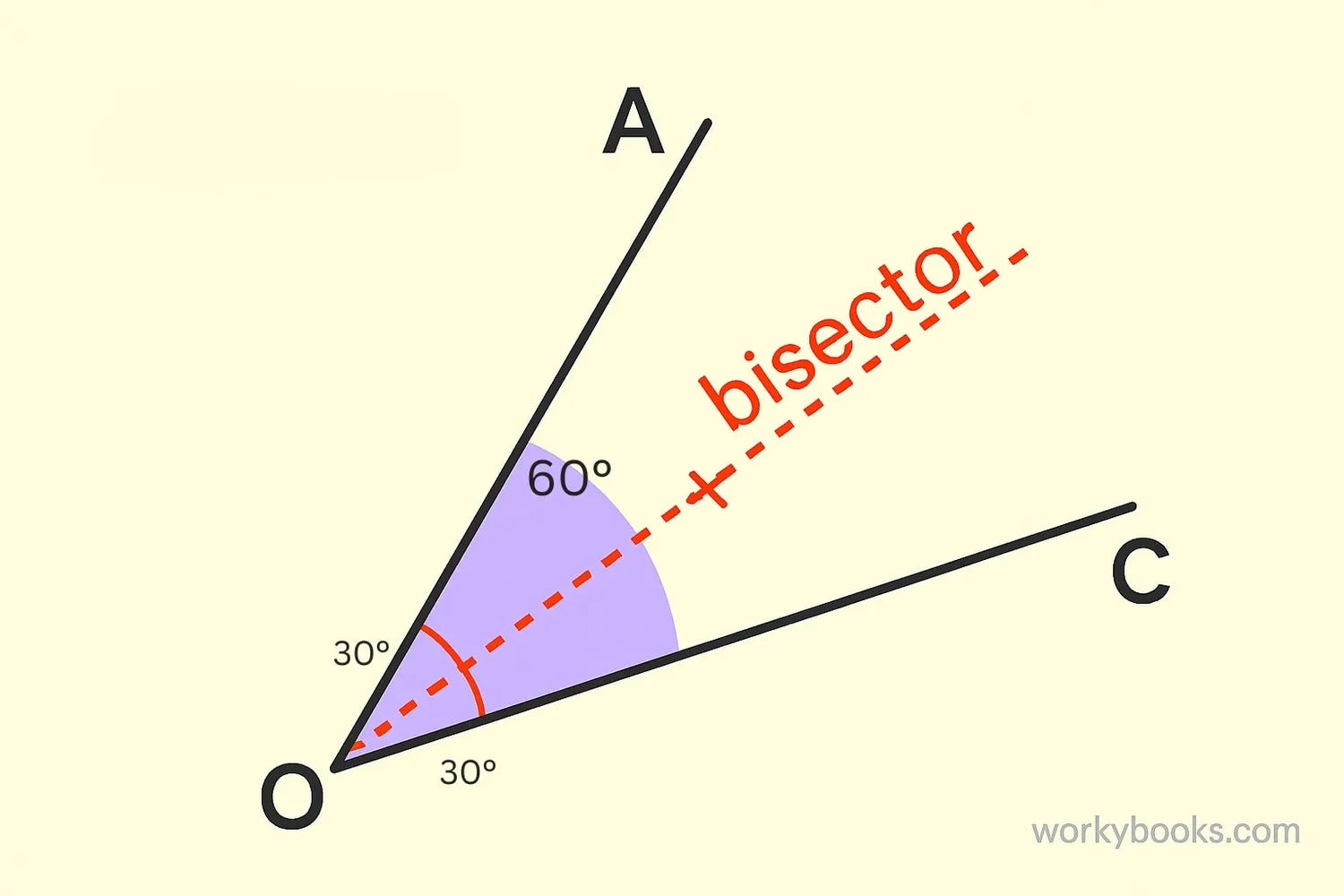
An angle bisector is a line or ray that divides an angle into two equal angles. Imagine you have a slice of pizza. If you cut it exactly in half from the tip to the crust, you're creating an angle bisector!
Every angle has exactly one angle bisector. This special line starts at the vertex (corner point) of the angle and extends outward. The angle bisector is important in geometry because it helps create equal angles and symmetrical shapes.
Angle bisectors are used in many real-world applications like architecture, engineering, and even sports. For example, when soccer players take a penalty kick, they try to aim at the angle bisector of the goal for the best chance of scoring.
Key Concept
An angle bisector divides an angle into two equal smaller angles. If the original angle is 90°, the bisector creates two 45° angles.
How to Construct an Angle Bisector
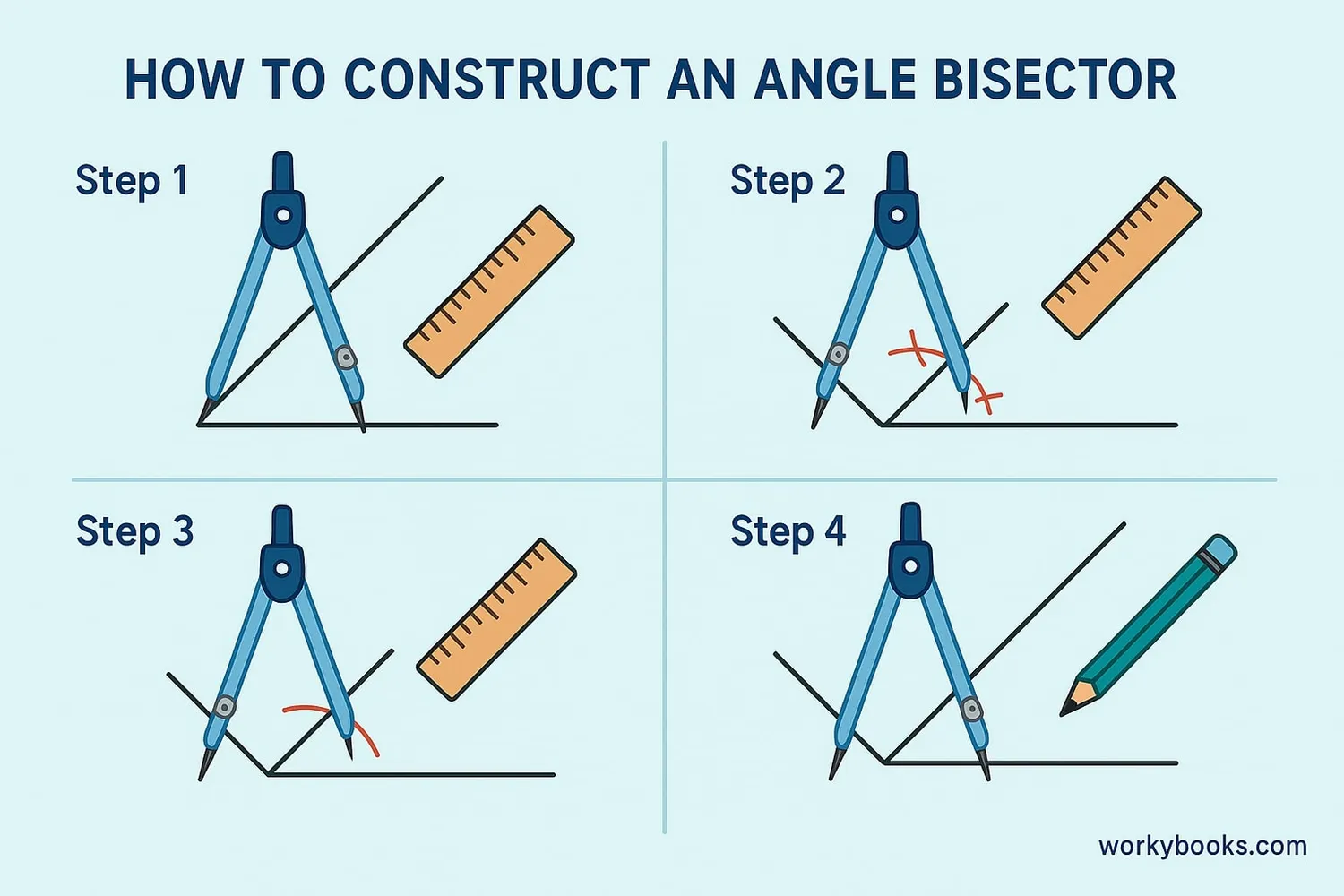
You can create an angle bisector using just a compass and straightedge. This is a fundamental geometric construction. Let's learn how to do it:
Draw an angle using your straightedge
Place compass at vertex, draw arc crossing both rays
From each intersection, draw arcs inside the angle
Connect vertex to intersection of arcs
Detailed Steps:
1. Start with angle BAC (angle at point A between points B and C).
2. Place your compass on point A and draw an arc that crosses both rays of the angle. Label these intersection points as D and E.
3. Place your compass on point D and draw an arc inside the angle. Without changing the compass width, place the compass on point E and draw another arc that crosses the first arc. Label this intersection F.
4. Draw a straight line from point A through point F. This line AF is your angle bisector!
Remember
When constructing an angle bisector, it's important to keep your compass at the same width when drawing the intersecting arcs in step 3.
Angle Bisector Theorem
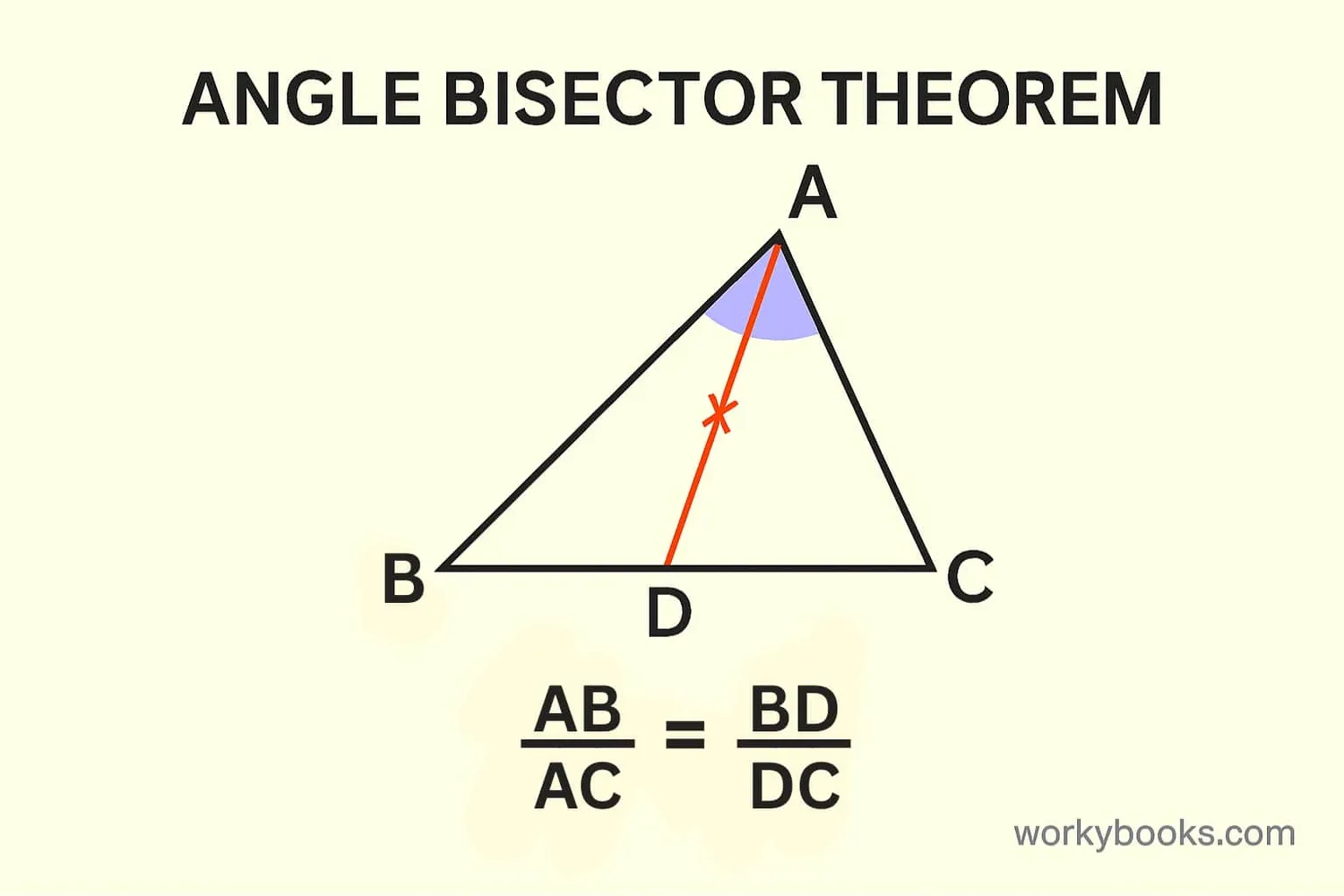
The angle bisector theorem is an important rule that connects the angle bisector to the sides of a triangle:
Angle Bisector Theorem
If a ray bisects an angle of a triangle, it divides the opposite side into segments proportional to the adjacent sides.
Example: In triangle ABC, if the bisector of angle A meets side BC at point D, then:
BD/DC = AB/AC
This means the ratio of the lengths of the two segments of the divided side equals the ratio of the other two sides of the triangle.
Practical Application: If AB = 6 cm, AC = 4 cm, and BC = 5 cm, then:
BD/DC = AB/AC = 6/4 = 3/2
Since BD + DC = BC = 5 cm, we can solve BD = 3 cm and DC = 2 cm.
Theorem Tip
The angle bisector theorem only works for triangles. It doesn't apply to other polygons directly.
Properties of Angle Bisectors
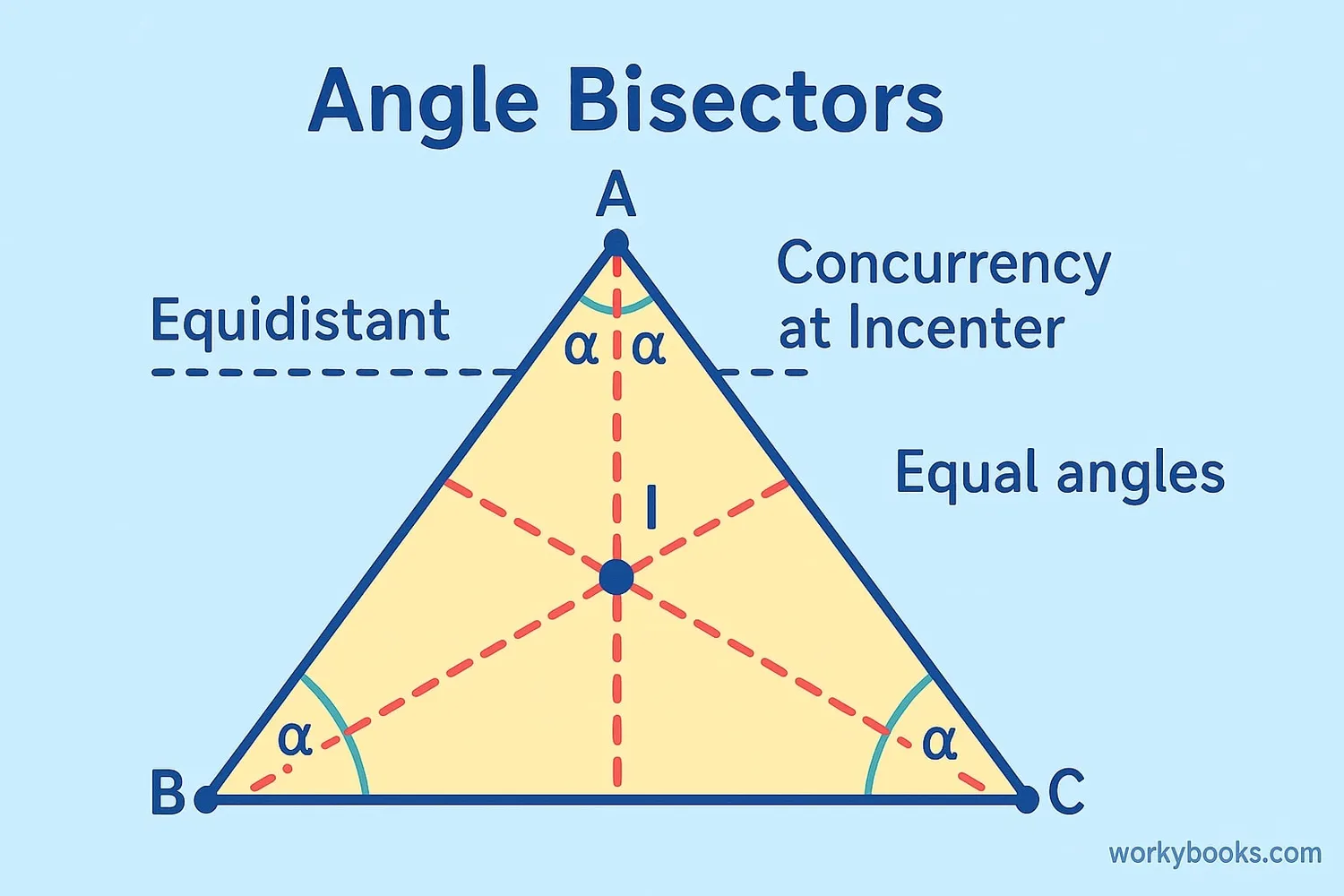
Angle bisectors have several important properties that make them useful in geometry:
- Equidistance: Any point on the angle bisector is equidistant (same distance) from the two sides of the angle.
- Triangle Incenter: The three angle bisectors of a triangle always meet at a single point called the incenter, which is the center of the triangle's incircle.
- Symmetry: The angle bisector is a line of symmetry for the angle.
- Perpendicularity: In a rhombus or square, the diagonals are angle bisectors and are perpendicular to each other.
- Equal Angles: The angles created by the bisector are always equal and each is half the measure of the original angle.
Special Property
In an equilateral triangle, all angle bisectors are also altitudes, medians, and perpendicular bisectors.
Real-World Examples
Angle bisectors aren't just for math class - they appear in many real-world situations:
Example 1: Soccer
When a player takes a penalty kick, the best position to aim is along the angle bisector of the goal. This gives the goalkeeper the least advantage.
Example 2: Architecture
Architects use angle bisectors to create symmetrical designs and ensure proper weight distribution in structures like roofs and bridges.
Example 3: Navigation
Navigators use the concept of angle bisectors when charting courses, especially when they need to find a midpoint direction between two points.
Example 4: Art and Design
Artists use angle bisectors to create balanced compositions and symmetrical patterns in their artwork.
Example 5: Robotics
Robots use angle bisector calculations to navigate efficiently between obstacles and reach their destinations.
Try This
Take a piece of paper and fold it so that two edges meet. The crease you make is an angle bisector!
Angle Bisector Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about angle bisectors:
Geometry Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Masters
The ancient Egyptians were using angle bisectors in pyramid construction as early as 2600 BC. Their precise measurements show advanced understanding of geometry.
Nature's Angles
Honeybees use angle bisectors when building honeycombs. The hexagonal cells have angles precisely bisected to create the most efficient storage space.
Space Geometry
NASA engineers use angle bisector principles when calculating spacecraft trajectories. Precise angle division helps spacecraft navigate efficiently through space.
Perfect Angles
The most precise angle bisector ever constructed was made by scientists at the National Institute of Standards and Technology, accurate to within 0.000001 degrees!





