Angles of Parallelogram - Definition, Examples, Quiz, FAQ, Trivia
Learn about parallelogram angles with simple explanations, properties, examples, and interactive quizzes
What is a Parallelogram?
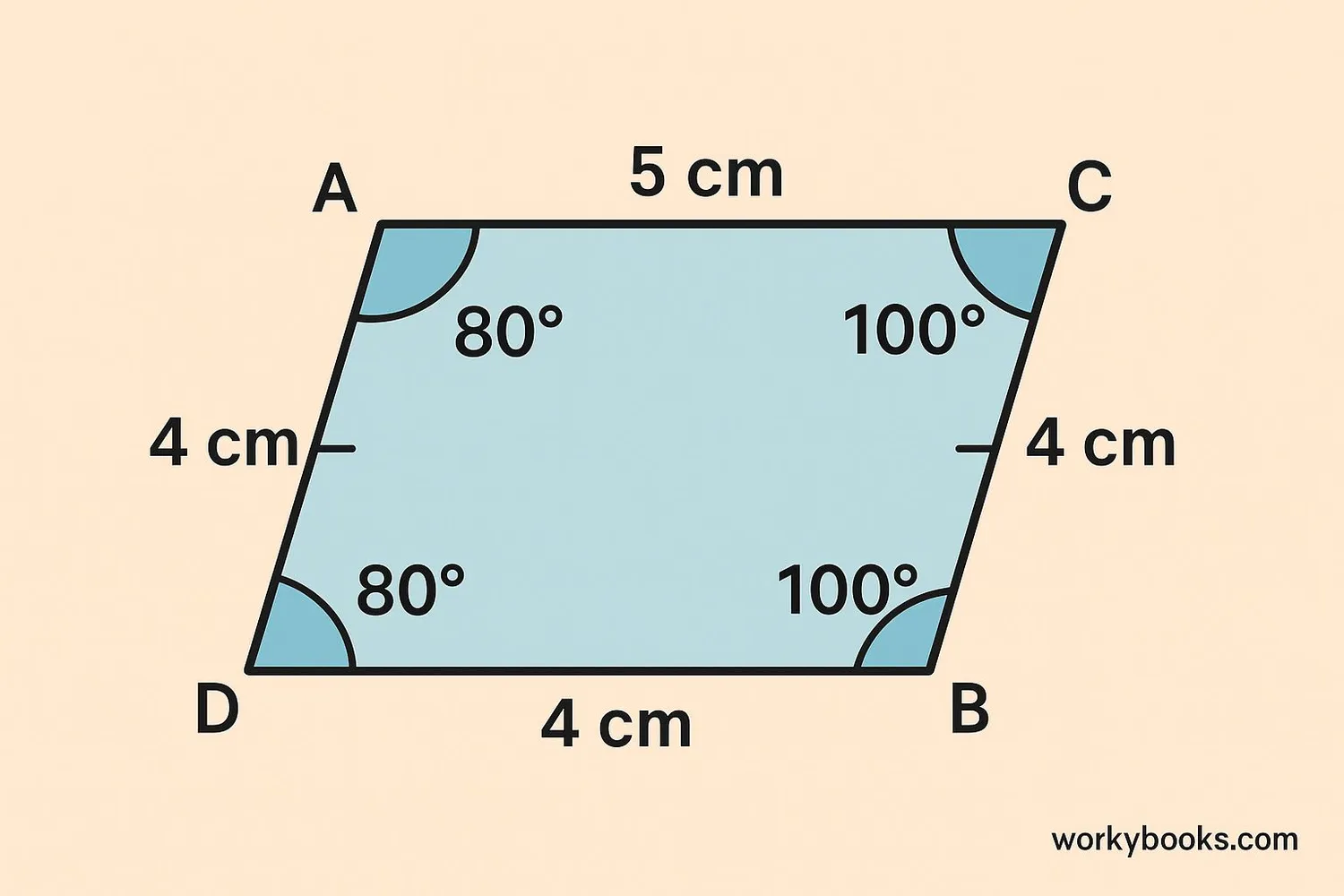
A parallelogram is a special type of quadrilateral (4-sided shape) where opposite sides are parallel and equal in length. This special shape has some amazing properties when it comes to its angles!
Think of it like a rectangle that's been pushed to one side. Even though it looks slanted, the angles follow special rules that make it easy to work with.
In any parallelogram:
- Opposite sides are equal in length
- Opposite angles are equal
- Consecutive angles add up to 180°
Key Concept
A parallelogram is a quadrilateral with two pairs of parallel sides. This simple definition leads to all its special angle properties.
Angle Properties of Parallelograms
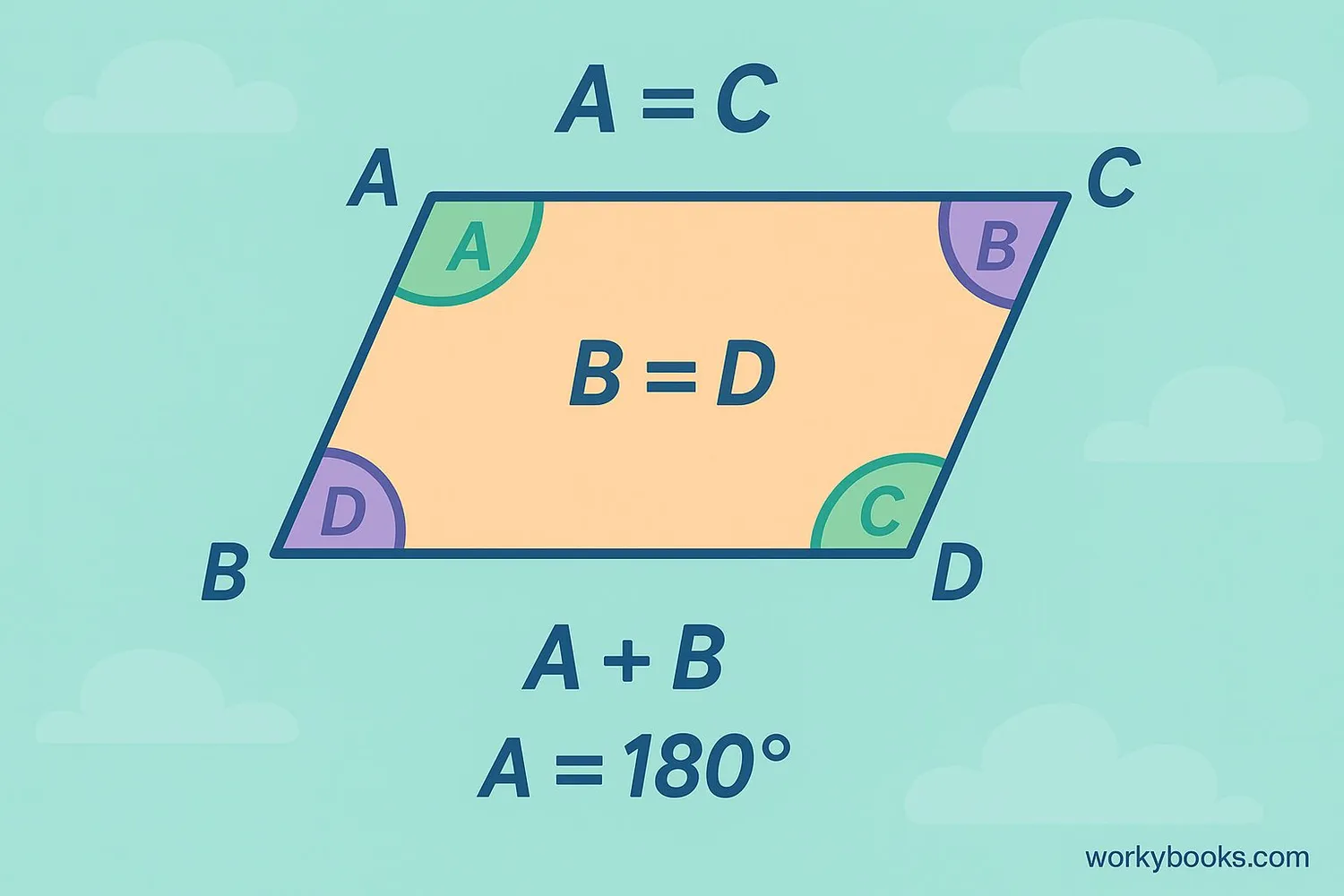
Parallelograms have two important angle properties that always hold true:
1. Opposite angles are equal: Angle A = Angle C and Angle B = Angle D
2. Consecutive angles are supplementary: This means they add up to 180°. For example:
- Angle A + Angle B = 180°
- Angle B + Angle C = 180°
- And so on for all adjacent angles
Why does this happen? When two parallel lines are crossed by another line (called a transversal), they create special angle relationships. In a parallelogram, each side acts as a transversal to the parallel sides.
Parallelogram Angle Theorem
Any two consecutive angles in a parallelogram add up to 180°
Remember
Because consecutive angles are supplementary, if you know one angle in a parallelogram, you can find all the others!
How to Find Missing Angles
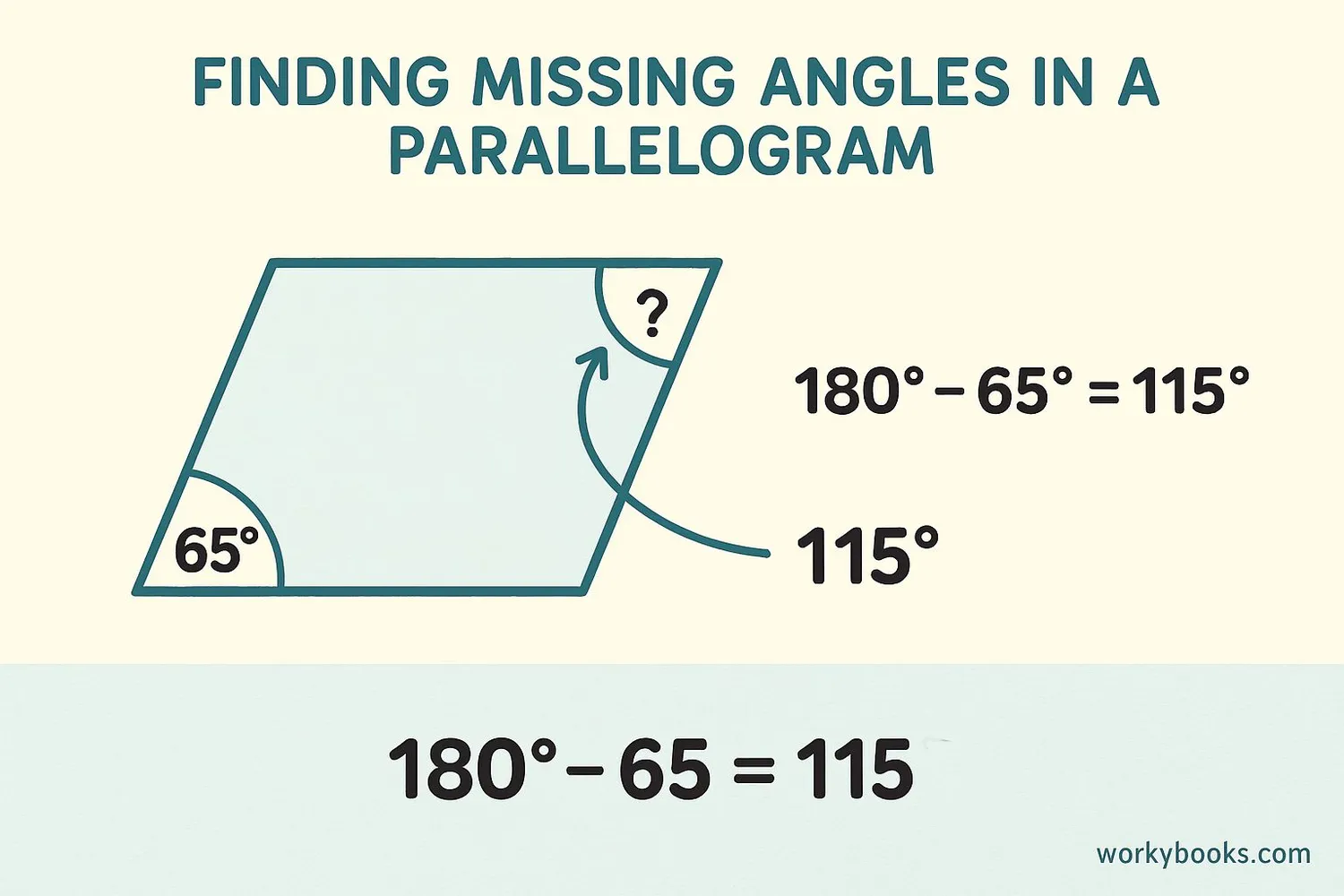
Finding missing angles in a parallelogram is easy when you remember the properties we learned:
Step 1: Identify what you know - at least one angle measurement
Step 2: Find the angle opposite to it - they're equal!
Step 3: Find the consecutive angles - subtract your known angle from 180° to find adjacent angles
Example: If one angle is 65°, then:
- The opposite angle is also 65°
- The adjacent angles are 180° - 65° = 115° each
So all angles are either 65° or 115°. Let's check: 65° + 115° = 180°, which matches our supplementary rule!
Tip
The sum of all interior angles in any quadrilateral is 360°. For a parallelogram, this means two angles are acute and two are obtuse (unless it's a rectangle).
Solved Examples
Let's practice with some examples:
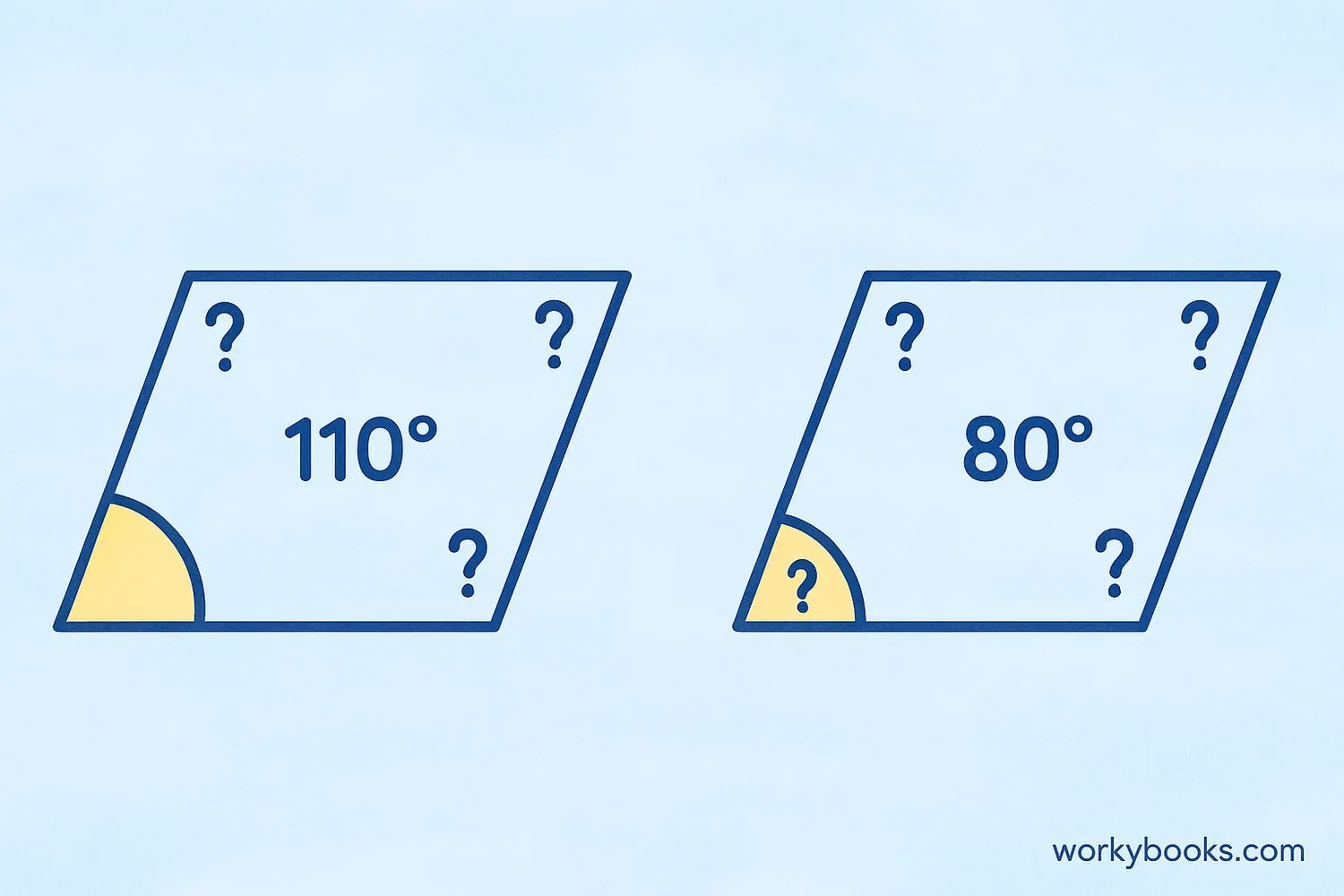
Example 1: In parallelogram PQRS, angle P = 110°. Find the other angles.
Solution:
- Angle R (opposite to P) = 110°
- Angle Q (adjacent to P) = 180° - 110° = 70°
- Angle S (opposite to Q) = 70°
Example 2: In parallelogram ABCD, angle B = 80°. Find angle D.
Solution:
- Angle D is opposite to angle B? No! Opposite angles are A-C and B-D.
- So angle D is opposite to angle B? Actually, opposite angles are equal, so angle D = angle B = 80°.
Example 3: In parallelogram LMNO, angle L = 55°. Find angle M.
Solution:
- Angle M is consecutive to angle L, so they are supplementary.
- Angle M = 180° - 55° = 125°
Remember
When labeling parallelograms, opposite angles are always equal, regardless of how the shape is rotated or labeled.
Practice Quiz
Test your understanding with these 5 questions about parallelogram angles:
Frequently Asked Questions
Here are answers to common questions about parallelogram angles:
Geometry Trivia
Discover interesting facts about parallelograms and geometry:
Ancient Geometry
The concept of parallelograms dates back to ancient Egypt, where surveyors used their properties to measure land after Nile River floods.
Real-World Applications
Parallelogram properties are used in engineering for structures like bridges and roofs, where stability is crucial.
The Parallelogram Law
In physics, the parallelogram law describes how to add two vectors. The diagonal of the parallelogram represents the sum of the vectors.
Special Parallelograms
A rhombus is a parallelogram with all sides equal. A rectangle is a parallelogram with all angles equal. A square is both a rhombus and a rectangle!





