Area of 2D Shapes - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate the area of squares, rectangles, triangles, circles and more with simple formulas and practice activities
What is Area?
Area is the amount of space inside a two-dimensional shape. Think of it as how many square units it would take to completely cover the shape without any gaps or overlaps.
Why is area important? We use area in many real-life situations:
- Calculating how much paint you need for a wall
- Determining the size of a carpet for a room
- Figuring out how much seed to buy for a garden
- Designing objects like books, phones, and furniture
Area is always measured in square units, like square centimeters (cm²), square inches (in²), or square meters (m²).
Key Concept
Area measures the surface covered by a 2D shape. The larger the area, the more space the shape covers!
Area of Common 2D Shapes
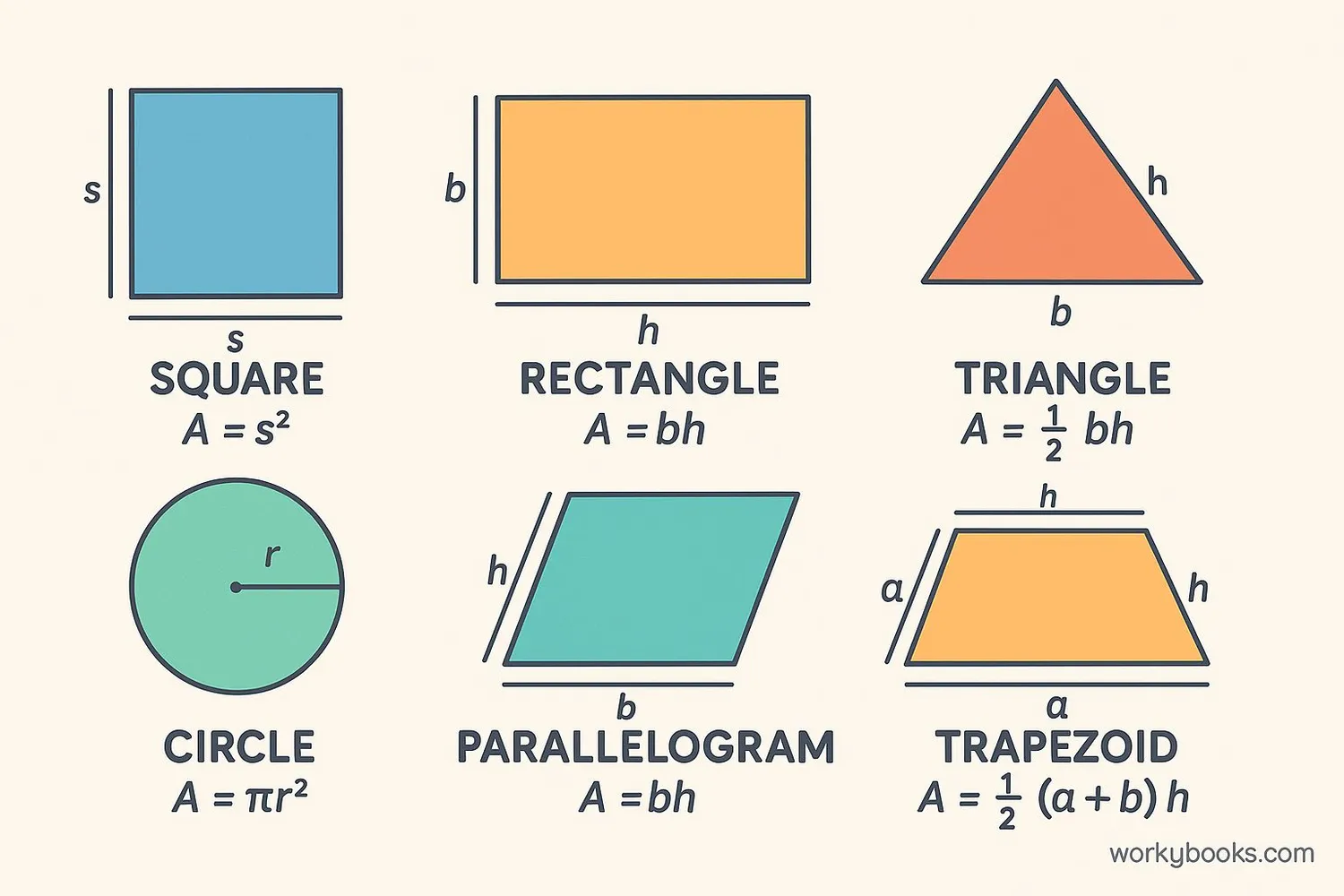
Different shapes have different area formulas. Let's look at the most common 2D shapes:
Square
All sides equal, all angles 90°
s = side length
Rectangle
Opposite sides equal, all angles 90°
l = length, w = width
Triangle
Three sides, three angles
b = base, h = height
Circle
Round shape, no corners
r = radius, π ≈ 3.14
Remember
The height of a shape is always perpendicular (at a 90° angle) to the base. This is especially important for triangles and parallelograms.
Area Formulas Reference
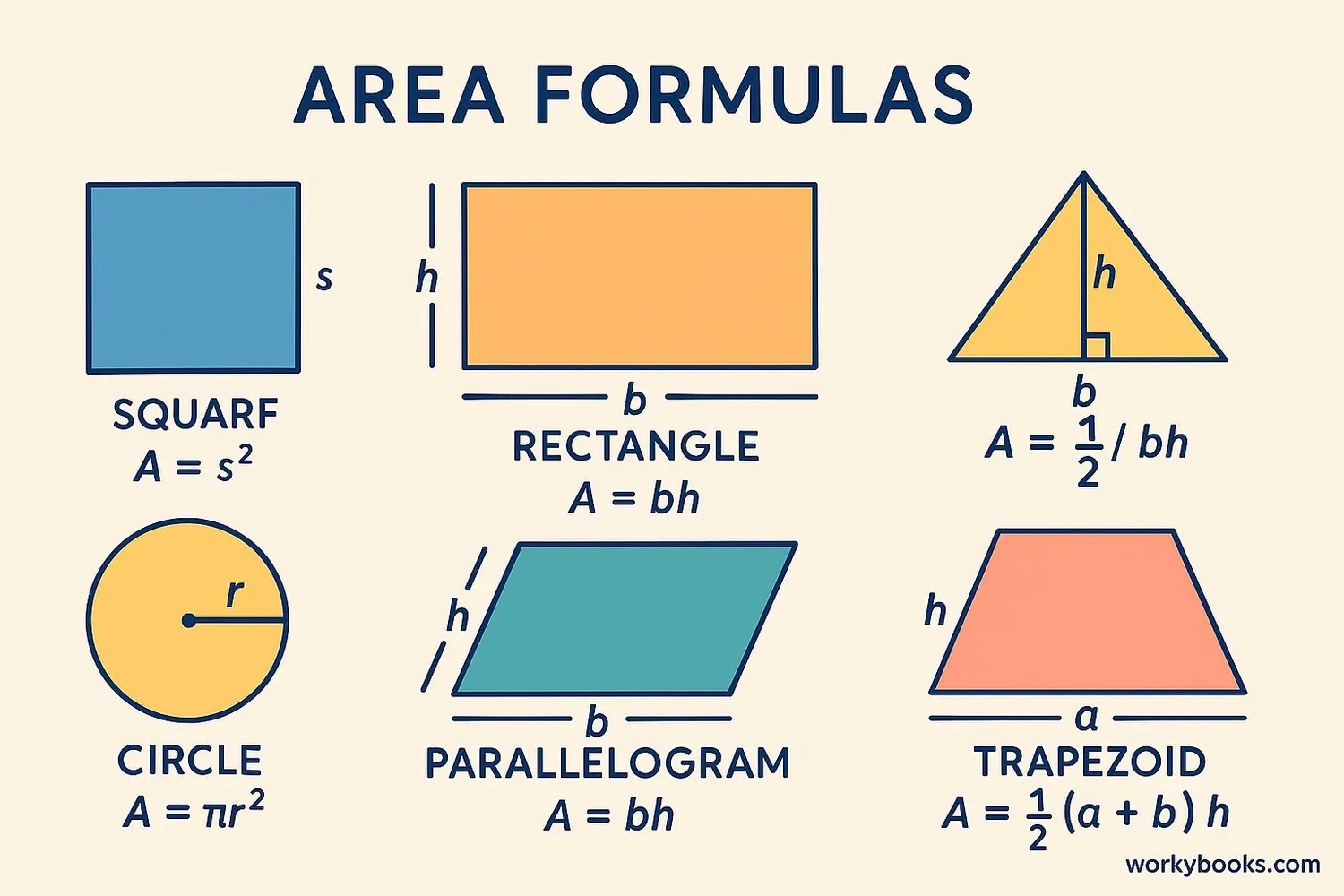
Here's a complete reference table for area formulas of common 2D shapes:
| Shape | Formula | Variables |
|---|---|---|
| Square | A = s² | s = side length |
| Rectangle | A = l × w | l = length, w = width |
| Triangle | A = ½ × b × h | b = base, h = height |
| Circle | A = πr² | r = radius, π ≈ 3.14159 |
| Parallelogram | A = b × h | b = base, h = height |
| Trapezoid | A = ½ × (b₁ + b₂) × h | b₁, b₂ = parallel sides, h = height |
| Rhombus | A = d₁ × d₂ × 0.5 | d₁, d₂ = diagonals |
Formula Tip
All area formulas require two measurements. For squares, you only need one because all sides are equal!
Area Calculation Examples
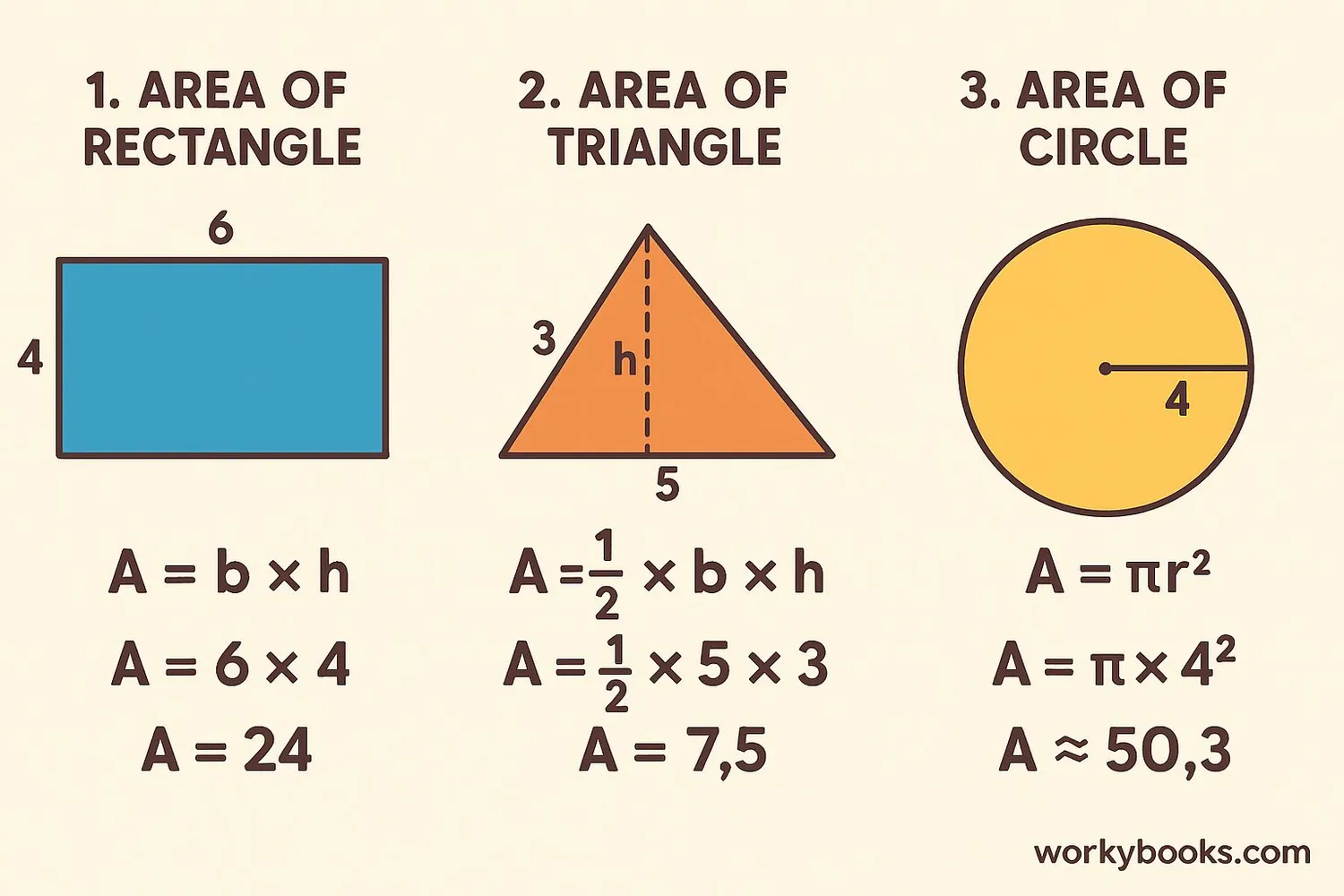
Let's practice calculating area with some examples:
Example 1: Rectangle
A classroom whiteboard is 120 cm long and 90 cm wide. What is its area?
Solution: Area = length × width = 120 cm × 90 cm = 10,800 cm²
Example 2: Triangle
A triangular sail has a base of 4 meters and height of 6 meters. What is its area?
Solution: Area = ½ × base × height = 0.5 × 4 m × 6 m = 12 m²
Example 3: Circle
A circular pizza has a radius of 15 cm. What is its area?
Solution: Area = πr² = 3.14 × (15 cm)² = 3.14 × 225 = 706.5 cm²
Example 4: Composite Shape
A garden consists of a rectangle (10m × 6m) and a semicircle on one end (diameter 6m). What is the total area?
Solution:
Rectangle area = 10 × 6 = 60 m²
Semicircle area = ½ × πr² = 0.5 × 3.14 × (3)² = 0.5 × 3.14 × 9 ≈ 14.13 m²
Total area = 60 + 14.13 = 74.13 m²
Practice Tip
Always include units in your answer! Area is always in square units (cm², m², etc.).
Area Calculation Quiz
Test your area calculation skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about area of 2D shapes:
Shape Trivia
Discover interesting facts about shapes and area:
Ancient Area Calculations
The ancient Egyptians developed early area formulas around 1850 BC to measure farmland after Nile River floods. They used ropes to measure and calculate areas of rectangular fields.
Circle Measurement
The value of π was first calculated by Archimedes around 250 BC. He approximated π by inscribing and circumscribing polygons around a circle and calculating their perimeters.
Largest 2D Shape
The largest 2D shape by area that can exist in our universe is limited only by the size of the universe itself! In mathematics, shapes can be infinitely large in theory.
Painting Records
The world's largest painting by area is 17,000 m² (over 4 acres), created in Dubai in 2020. That's equivalent to about 2.5 football fields!





