Area of a Pentagon - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate the area of pentagons with easy explanations, formulas, and practice activities
What is a Pentagon?
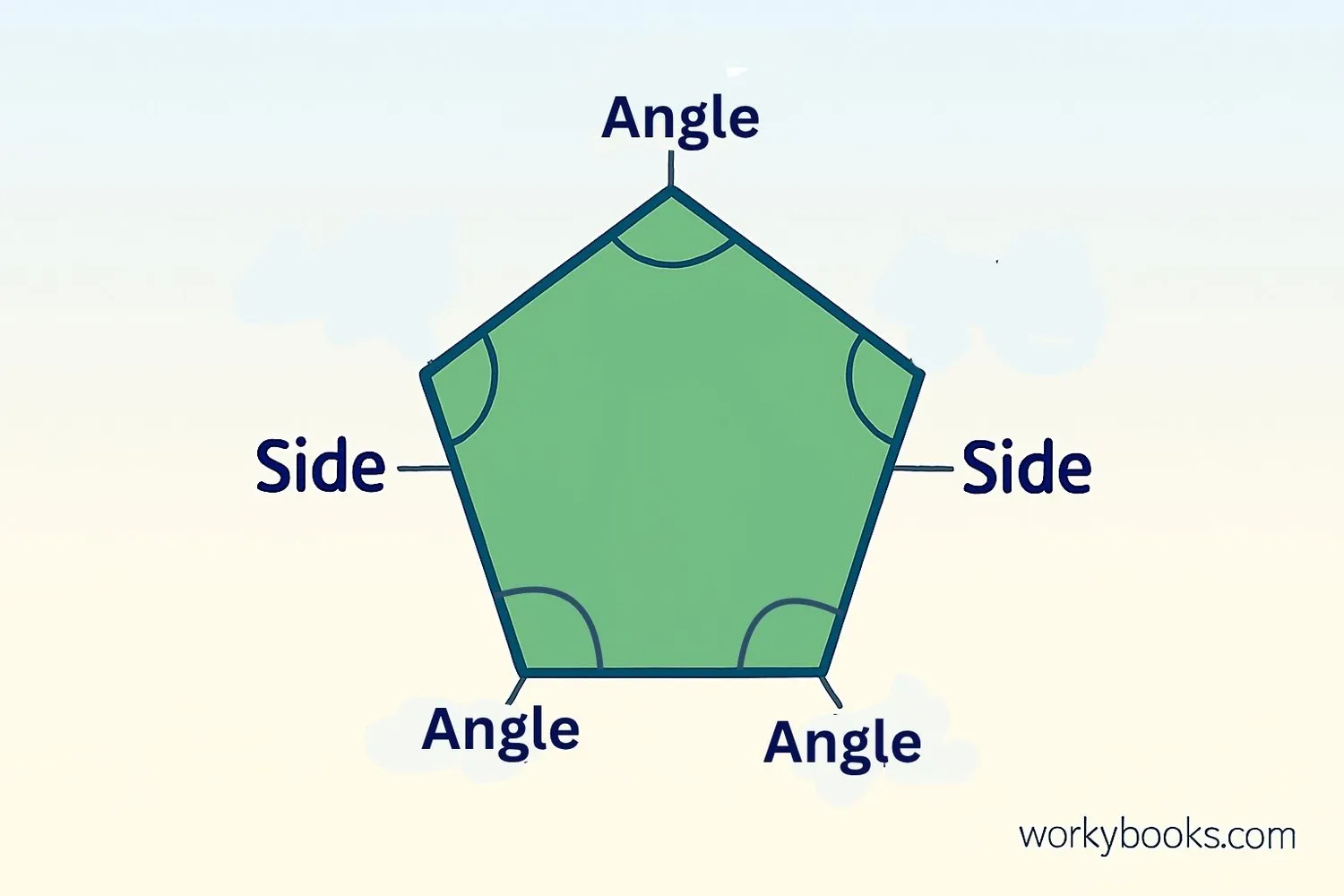
A pentagon is a special polygon with five sides and five angles. The word "pentagon" comes from the Greek words "pente" meaning five and "gonia" meaning angle.
Pentagons are all around us! You can see them in:
- Home plate in baseball
- The shape of some flowers
- Certain types of nuts and bolts
- Architectural designs like the Pentagon building
To find the area of a pentagon, we need to measure how much space is inside its five sides. This is especially important for regular pentagons where all sides and angles are equal.
Key Concept
All pentagons have five straight sides and five angles, but only regular pentagons have equal sides and angles.
Types of Pentagons
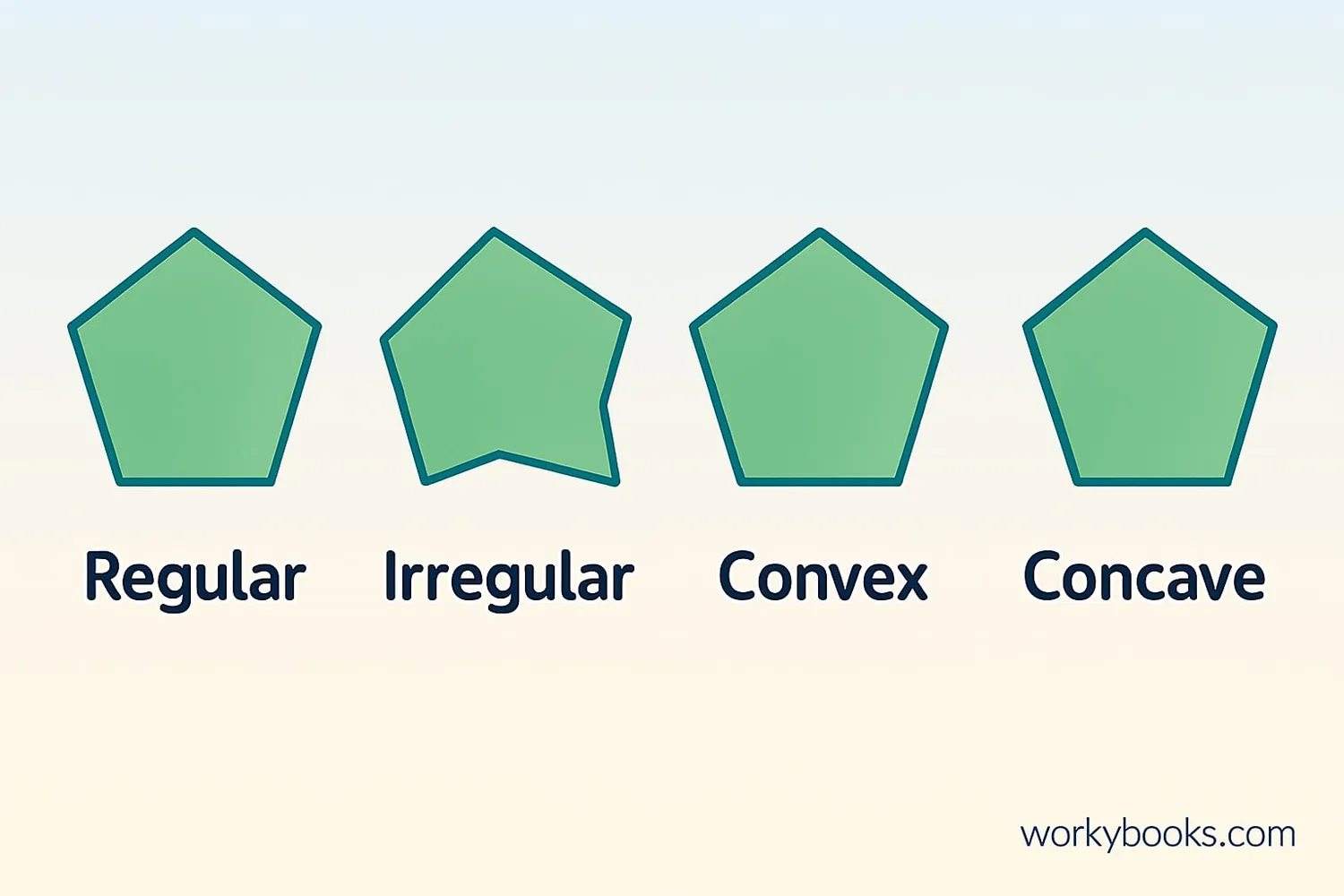
Pentagons come in different forms. Understanding these types helps us calculate area correctly:
Regular Pentagon: All five sides are equal length, and all five angles are equal (108° each). These have symmetry and are the easiest to calculate area for.
Irregular Pentagon: Sides and angles are not equal. These require different methods to calculate area.
Convex Pentagon: All interior angles are less than 180° and all vertices point outward. You can draw a straight line between any two points without leaving the shape.
Concave Pentagon: At least one interior angle is greater than 180° and at least one vertex points inward. These have a "caved-in" appearance.
Remember
Most formulas for pentagon area are designed for regular pentagons. Irregular pentagons require dividing into triangles and other shapes.
Area of a Regular Pentagon
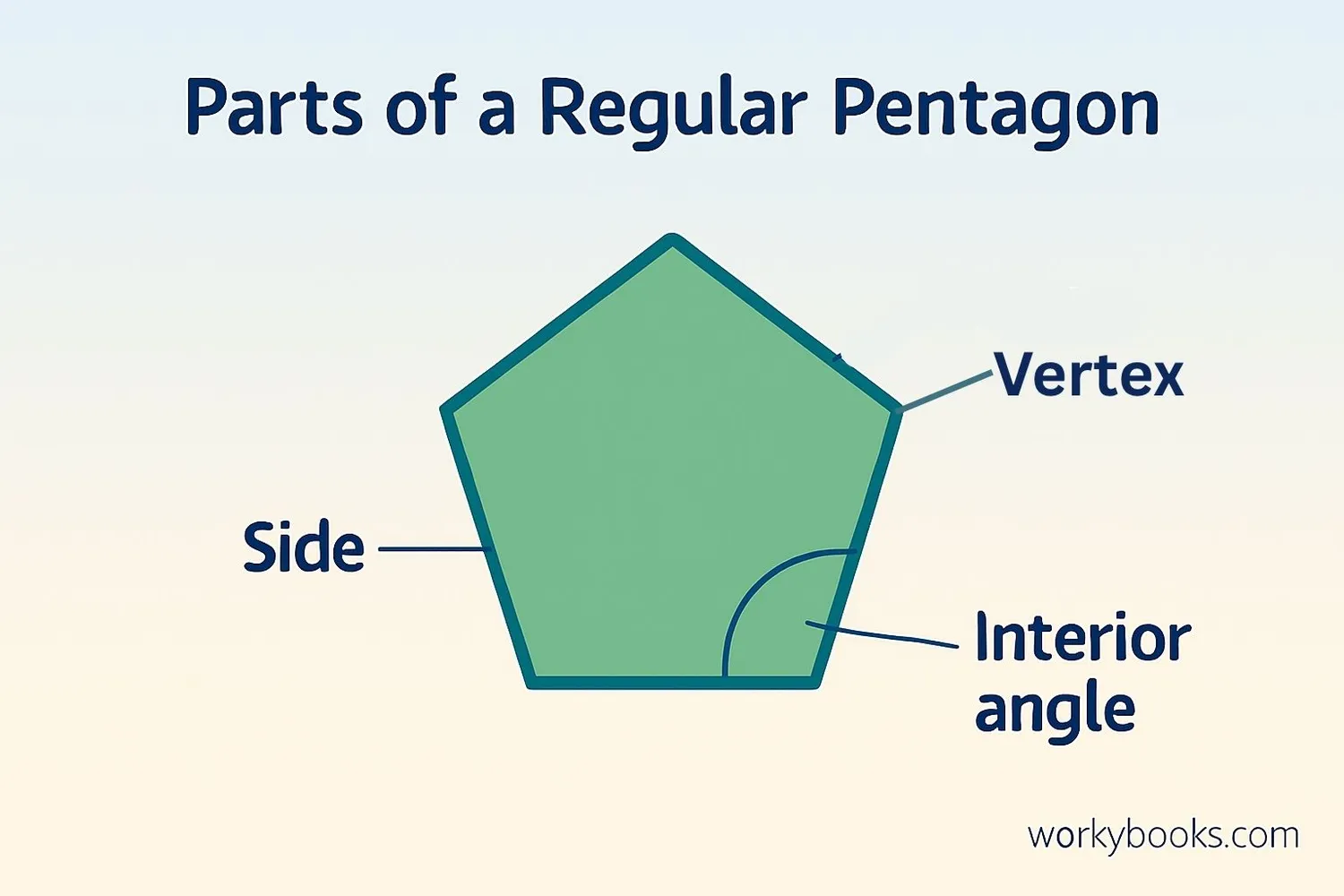
For regular pentagons, we have two main ways to calculate area:
Using Apothem and Perimeter
The apothem (a) is a line from the center to the middle of a side, perpendicular to that side.
Using Only Side Length
Where s is the length of one side. This formula uses the mathematical constant √5 (square root of 5).
Step 1: Find perimeter → Perimeter = 5 × 6 = 30 cm
Step 2: Apply formula → Area = ½ × 30 × 4.13
Step 3: Calculate → Area = 61.95 cm²
Remember
The apothem is always perpendicular to the side it touches. For a regular pentagon, all apothems are equal.
Area of an Irregular Pentagon
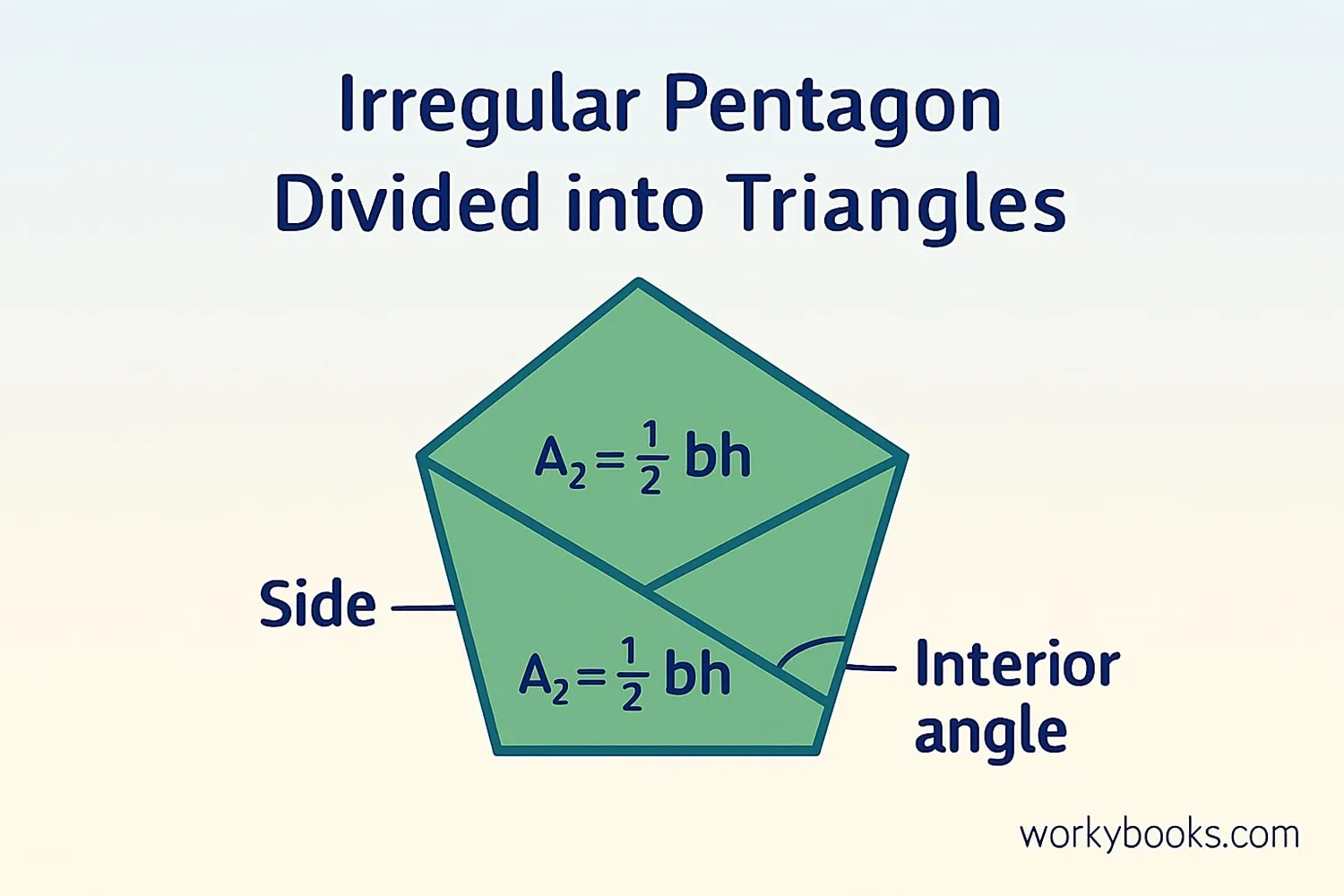
For irregular pentagons (where sides and angles are different), we use a different approach:
1. Divide the pentagon into triangles and other shapes (usually three triangles)
2. Calculate the area of each triangle
3. Add all the areas together
Example: Find the area of an irregular pentagon divided into three triangles:
Triangle 1: Base = 4 cm, Height = 3 cm → Area = ½ × 4 × 3 = 6 cm²
Triangle 2: Base = 5 cm, Height = 4 cm → Area = ½ × 5 × 4 = 10 cm²
Triangle 3: Base = 6 cm, Height = 4 cm → Area = ½ × 6 × 4 = 12 cm²
Total Area = 6 + 10 + 12 = 28 cm²
Helpful Tip
You can divide irregular pentagons into any combination of triangles and rectangles that makes calculation easier.
Real-World Examples
Let's practice with some real-world examples:
Example 1: A baseball home plate is a pentagon with side lengths of 17 cm, 17 cm, 17 cm, 17 cm, and 25.5 cm. If divided into a rectangle and two triangles, with rectangle area 289 cm² and each triangle 72.25 cm², what's the total area?
Solution: 289 + 72.25 + 72.25 = 433.5 cm²
Example 2: A regular pentagon-shaped tile has sides measuring 10 cm. Using the formula with √5 ≈ 2.236, what is its area?
Solution: Area = (¼) × √(5(5+2×2.236)) × 10² ≈ (0.25) × √(5×9.472) × 100 ≈ (0.25) × √47.36 × 100 ≈ (0.25) × 6.88 × 100 ≈ 172 cm²
Example 3: A pentagonal garden has been divided into three triangles with areas 15 m², 20 m², and 18 m². What is the total area of the garden?
Solution: 15 + 20 + 18 = 53 m²
Try measuring pentagon-shaped objects around you and calculate their area!
Remember
For real-world applications, always include units (cm², m², etc.) with your area calculations.
Pentagon Area Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about pentagons:
Pentagon Trivia
Discover interesting facts about pentagons:
Nature's Pentagons
Many flowers like morning glories and periwinkles have pentagonal symmetry. Starfish typically have five arms arranged in pentagonal symmetry.
The Pentagon Building
The United States Pentagon is the world's largest low-rise office building. It has five sides, five floors above ground, and five ring corridors per floor.
Golden Ratio Connection
In a regular pentagon, the ratio of a diagonal to a side is the golden ratio (approximately 1.618). This appears in many natural patterns.
Home Plate
In baseball, home plate is a pentagon with two right angles and three other angles. This unique shape helps define the strike zone.





