Area of a Quadrilateral - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate the area of different quadrilaterals with formulas, examples, and interactive activities
What is a Quadrilateral?
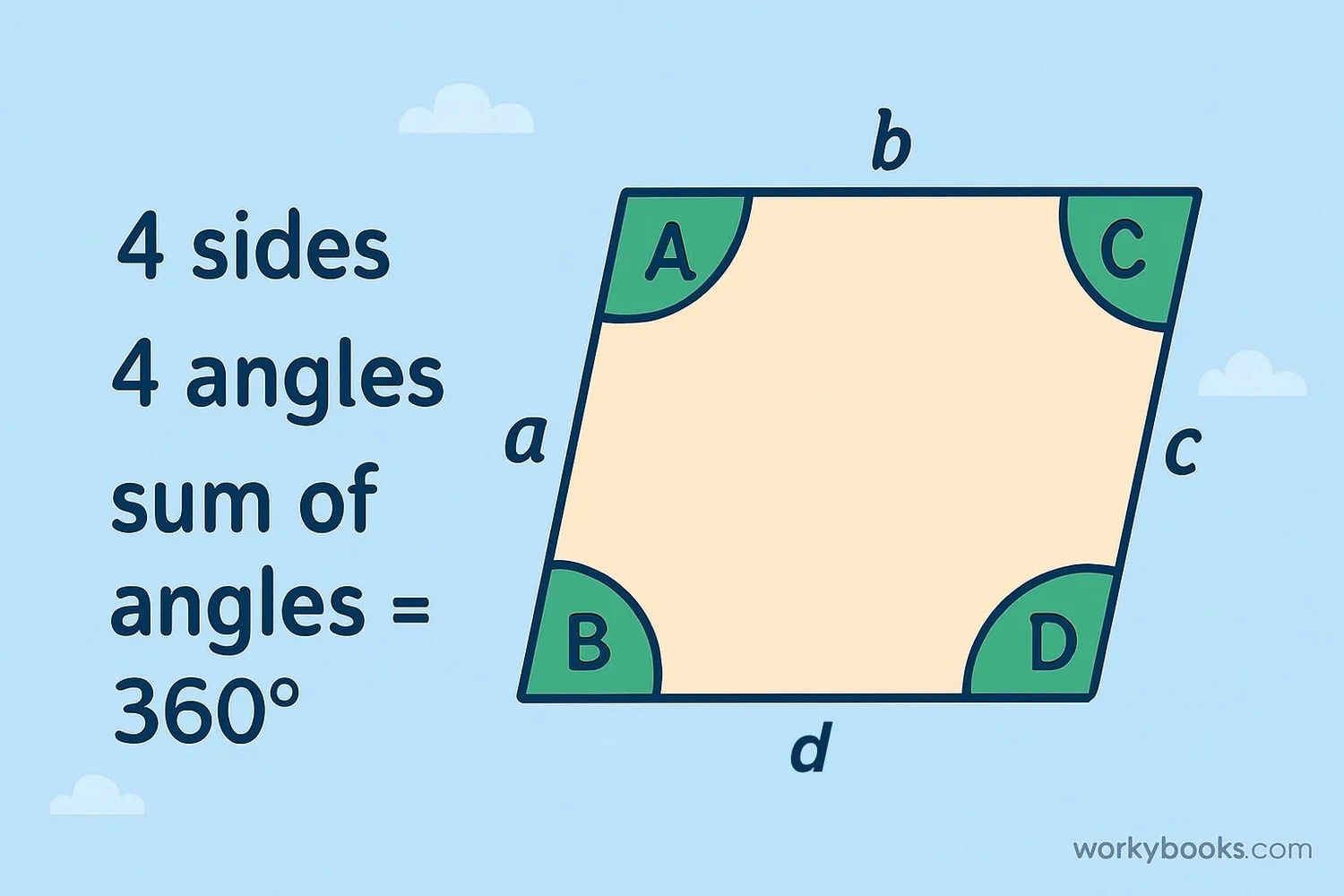
A quadrilateral is a polygon with four sides, four angles, and four vertices (corners). The word "quadrilateral" comes from Latin words "quadri" meaning four and "latus" meaning side.
All quadrilaterals have these properties:
- Four sides (edges)
- Four vertices (corners)
- Four interior angles
- The sum of all interior angles is always 360 degrees
Quadrilaterals are everywhere in our daily lives - windows, doors, books, and computer screens are all quadrilaterals!
Key Concept
All quadrilaterals have four straight sides that connect to form a closed shape. The sum of their interior angles is always 360 degrees.
Types of Quadrilaterals
There are several special types of quadrilaterals, each with their own unique properties:
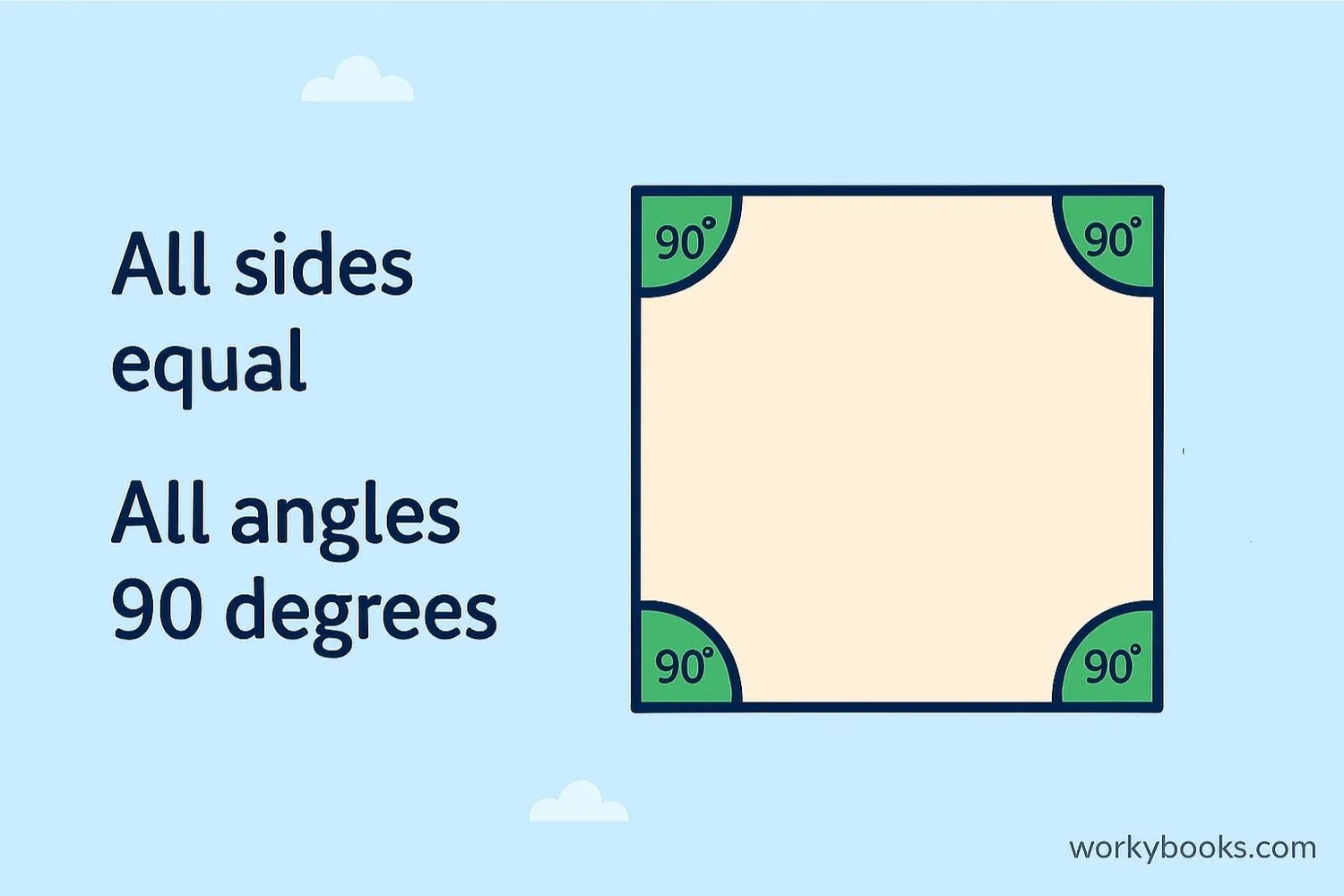
Square
All sides equal, all angles 90°.
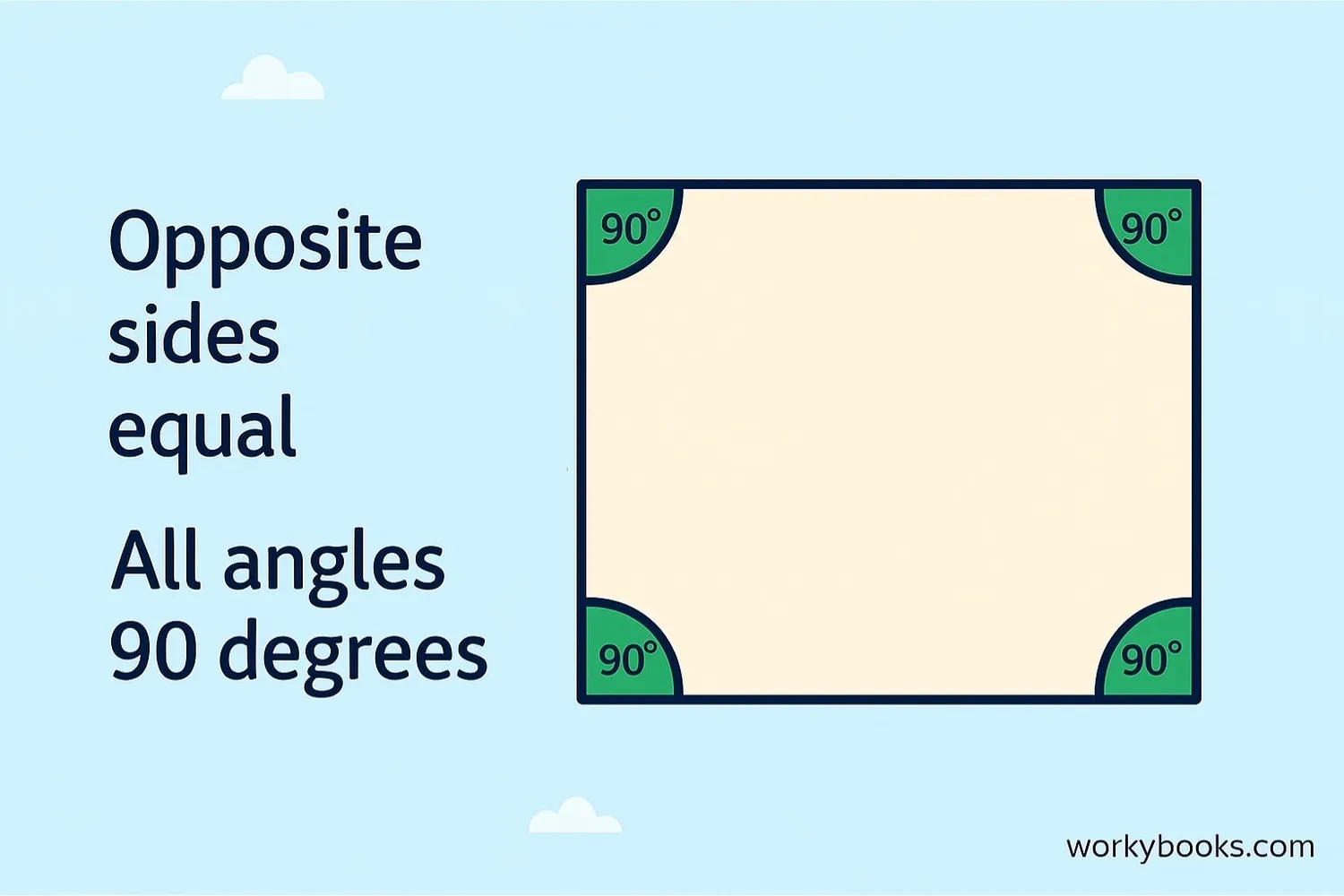
Rectangle
Opposite sides equal, all angles 90°.
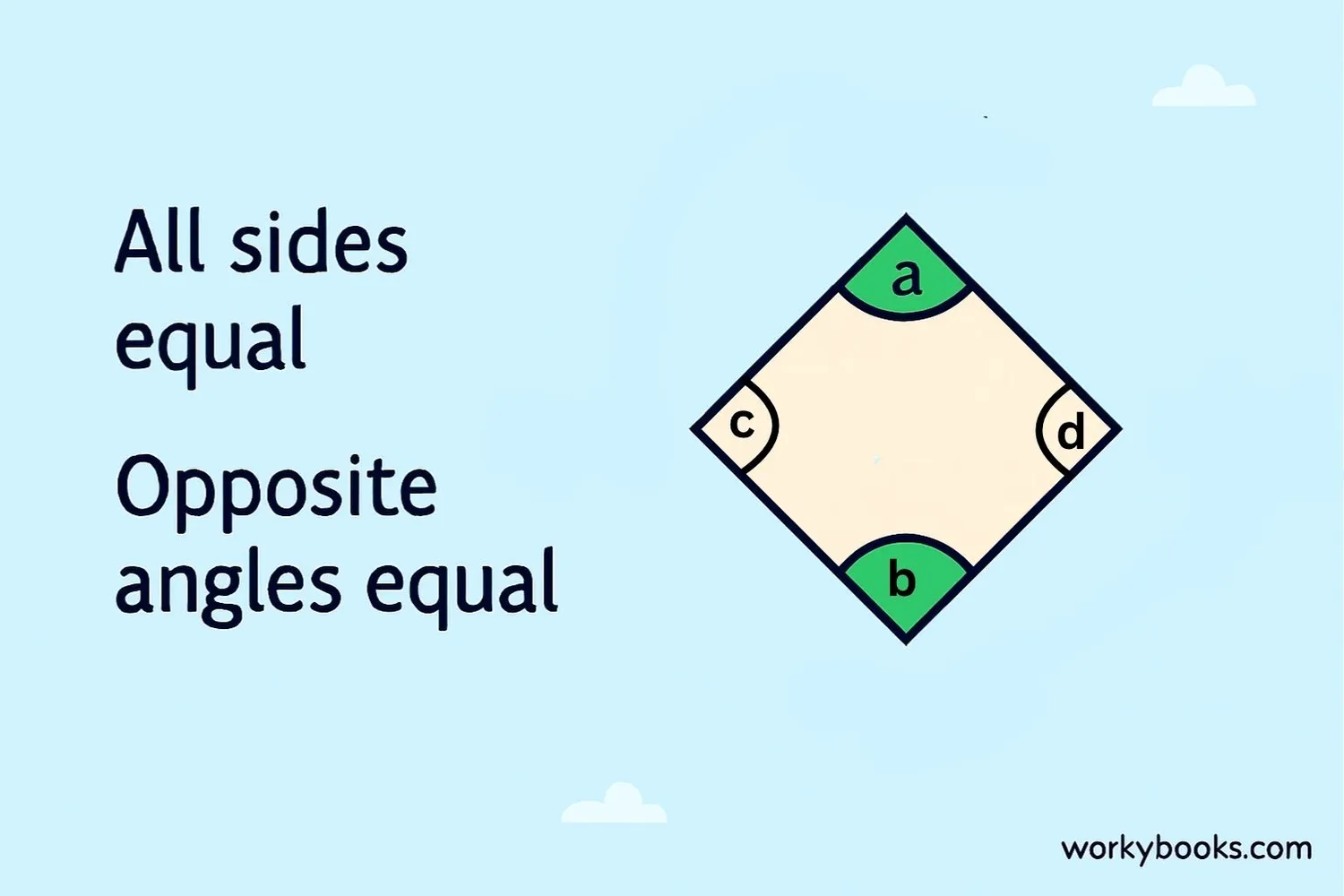
Rhombus
All sides equal, opposite angles equal.
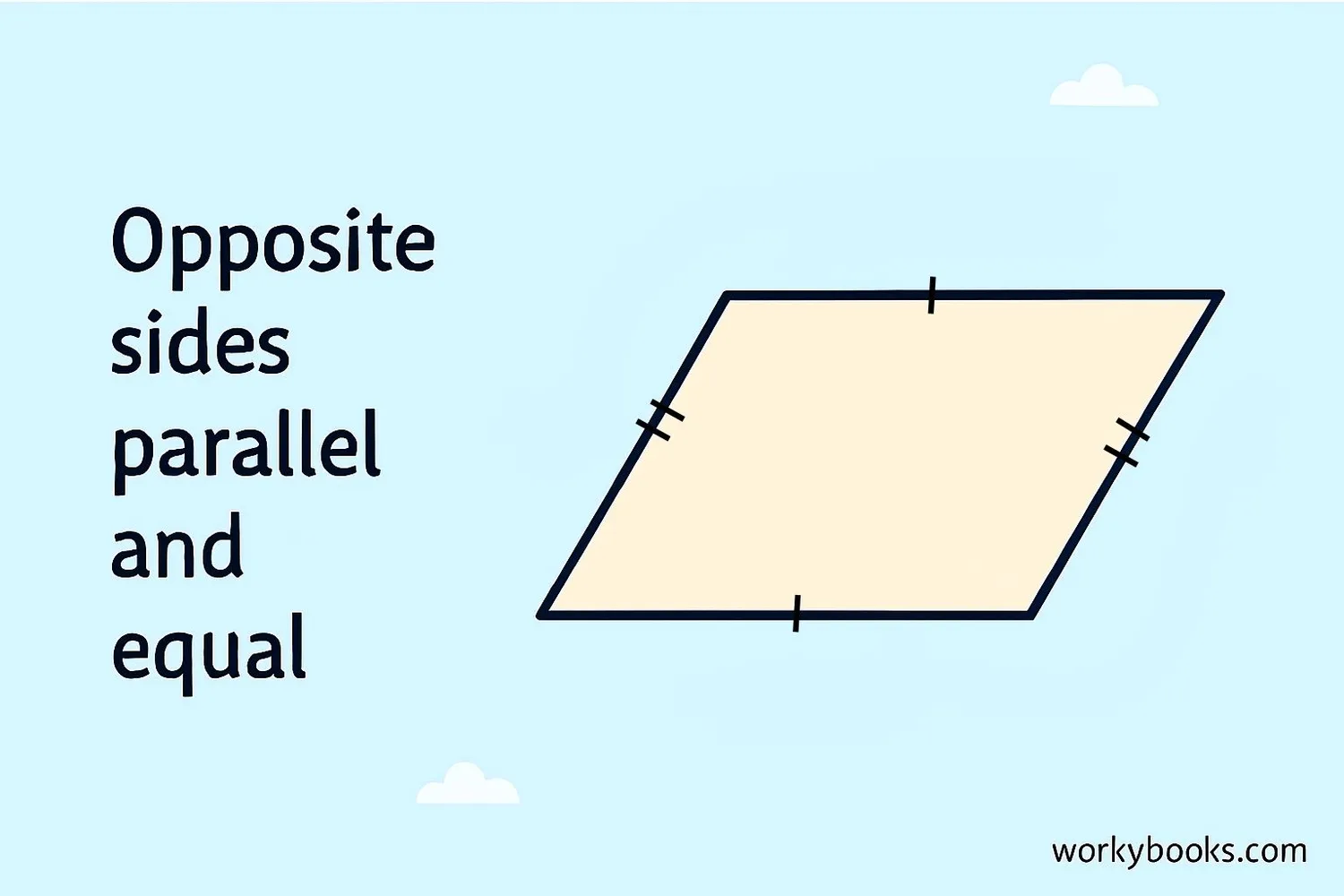
Parallelogram
Opposite sides parallel and equal.
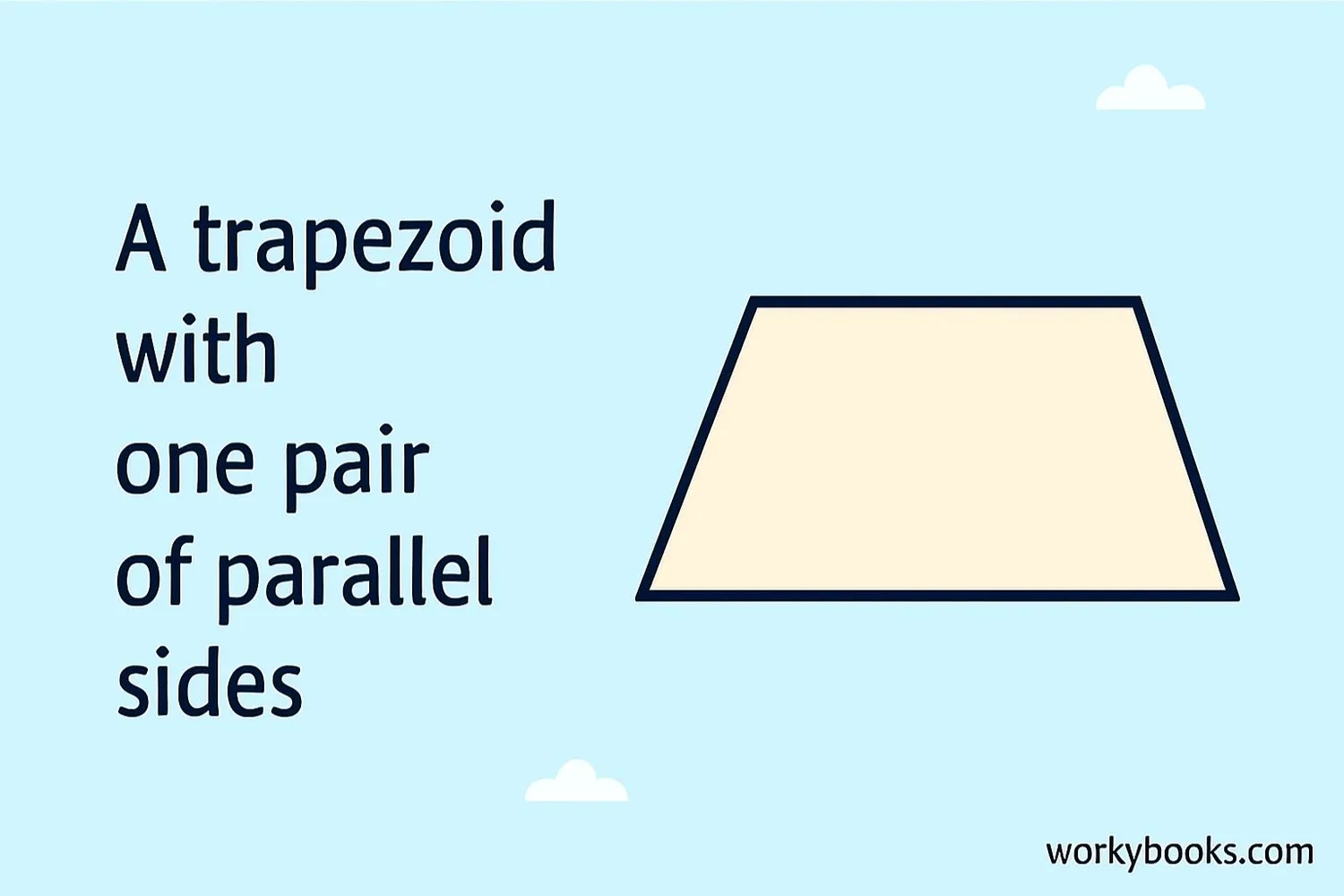
Trapezoid
One pair of parallel sides.
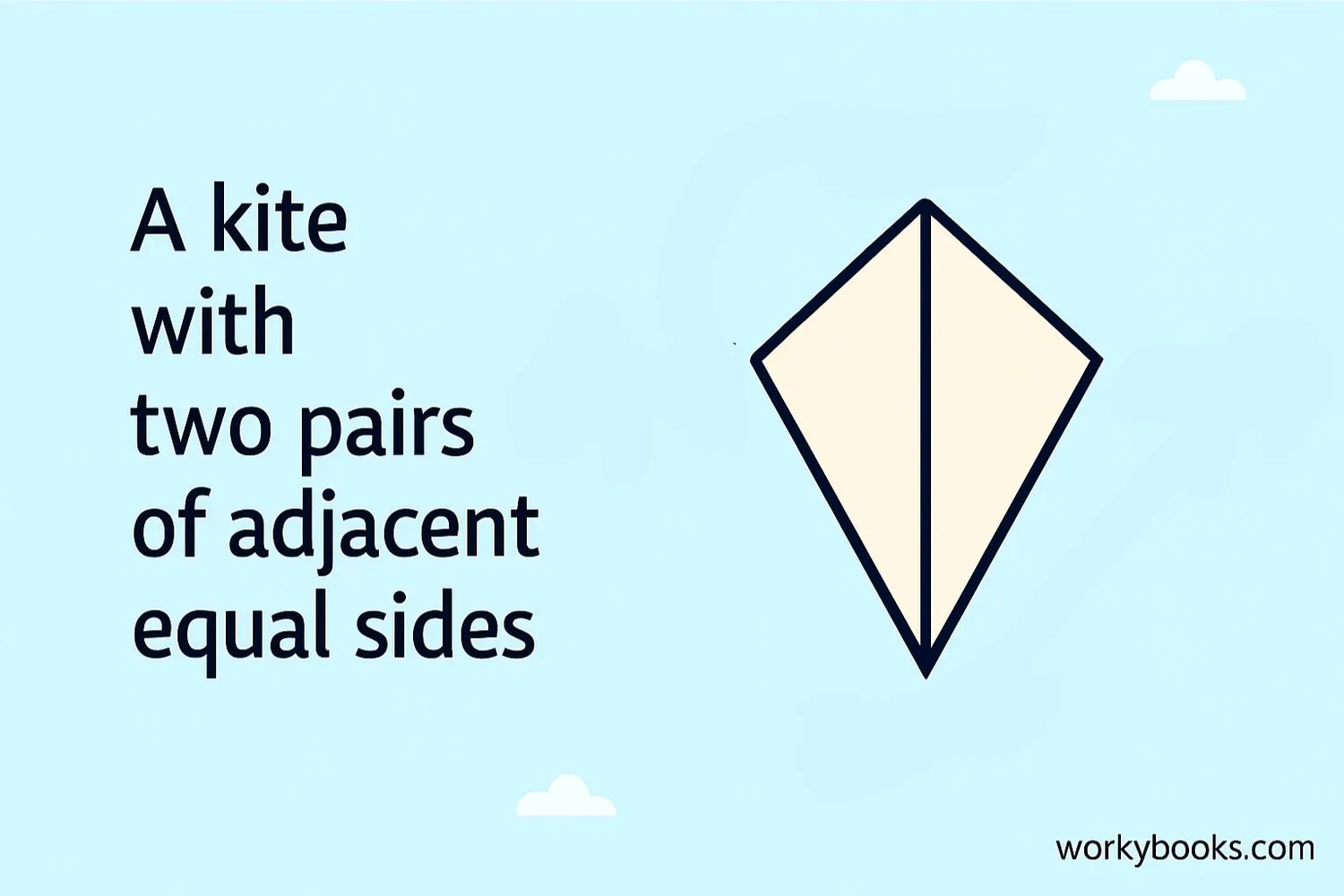
Kite
Two pairs of adjacent equal sides.
Remember
Some quadrilaterals can be classified in multiple categories. For example, a square is also a rectangle, rhombus, and parallelogram!
Area Formulas
Each type of quadrilateral has its own formula for calculating area:
Square
Since all sides are equal
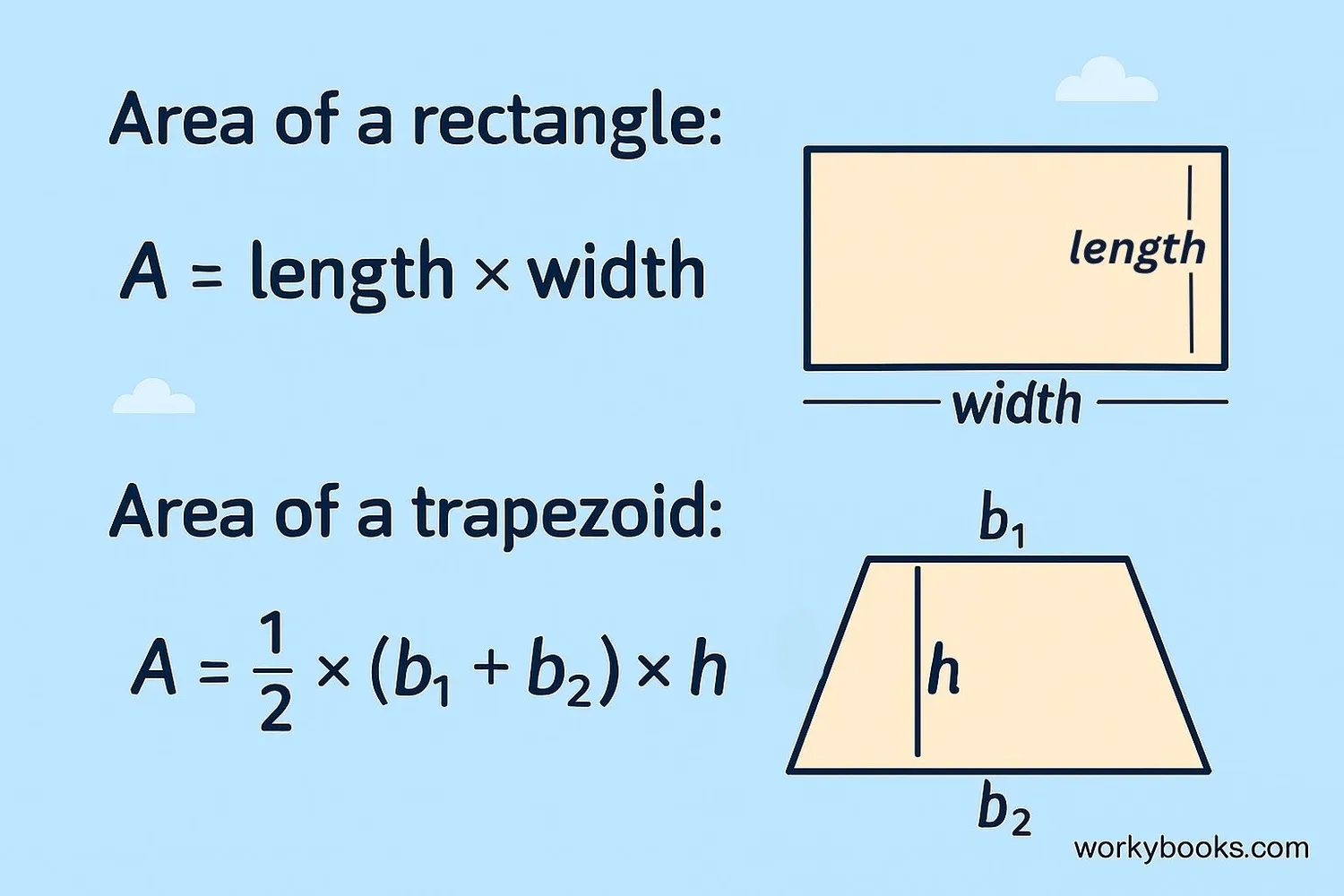
Rectangle
Multiply length and width
Rhombus
d₁ and d₂ are diagonals
Parallelogram
Height is perpendicular to base
Trapezoid
b₁ and b₂ are parallel sides
Kite
d₁ and d₂ are diagonals
General Quadrilateral Formula
For any quadrilateral, you can divide it into two triangles and add their areas:
How to Calculate Area
Let's learn how to calculate area step by step:
Step 1: Identify the type of quadrilateral
Determine which special quadrilateral you have (square, rectangle, etc.)
Step 2: Measure the required dimensions
Depending on the type, you may need sides, height, or diagonals
Step 3: Apply the correct formula
Use the appropriate area formula for your quadrilateral
Example: Finding area of a rectangle
A rectangle has length 8 cm and width 5 cm.
Area = length × width = 8 cm × 5 cm = 40 cm²
Example: Finding area of a trapezoid
A trapezoid has parallel sides 6 cm and 10 cm, height 4 cm.
Area = ½ × (6 cm + 10 cm) × 4 cm = ½ × 16 cm × 4 cm = 32 cm²
Area Units
Area is always measured in square units (cm², m², etc.). Remember to include the square unit in your answer!
Real-World Examples
Quadrilaterals are all around us! Let's practice with some real-world examples:
Example 1: Soccer Field
A rectangular soccer field is 100 meters long and 60 meters wide.
Area = length × width = 100 m × 60 m = 6,000 m²
Example 2: Kite
A kite has diagonals measuring 40 cm and 60 cm.
Area = (d₁ × d₂) ÷ 2 = (40 cm × 60 cm) ÷ 2 = 1,200 cm²
Example 3: Garden Plot
A trapezoidal garden has parallel sides 8 m and 12 m, with height 5 m.
Area = ½ × (8 m + 12 m) × 5 m = ½ × 20 m × 5 m = 50 m²
Example 4: Floor Tile
A square floor tile has sides of 30 cm.
Area = side × side = 30 cm × 30 cm = 900 cm²
Practice Tip
Look for quadrilaterals around your home and school. Measure their dimensions and practice calculating their areas!
Area Calculation Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about quadrilaterals and their areas:
Geometry Trivia
Discover interesting facts about quadrilaterals and geometry:
Ancient Geometry
The ancient Egyptians were using geometry to measure land areas as early as 3000 BC. They needed to re-establish field boundaries after the annual Nile floods.
Largest Quadrilateral
The largest man-made quadrilateral is the rectangular Kaesong Industrial Region in North Korea, covering over 20 million square meters.
Quadrilateral Angles
The sum of interior angles in any quadrilateral is always 360 degrees. This is because every quadrilateral can be divided into two triangles (180° + 180° = 360°).
Quadrilaterals in Nature
While most natural shapes are curved, some minerals like pyrite form cubic crystals which are perfect quadrilaterals when viewed from certain angles.





