Area of a Semicircle - Definition, Examples, Quiz, FAQ, Trivia
Learn about semicircles with simple explanations, formulas, examples, and practice activities
What is a Semicircle?

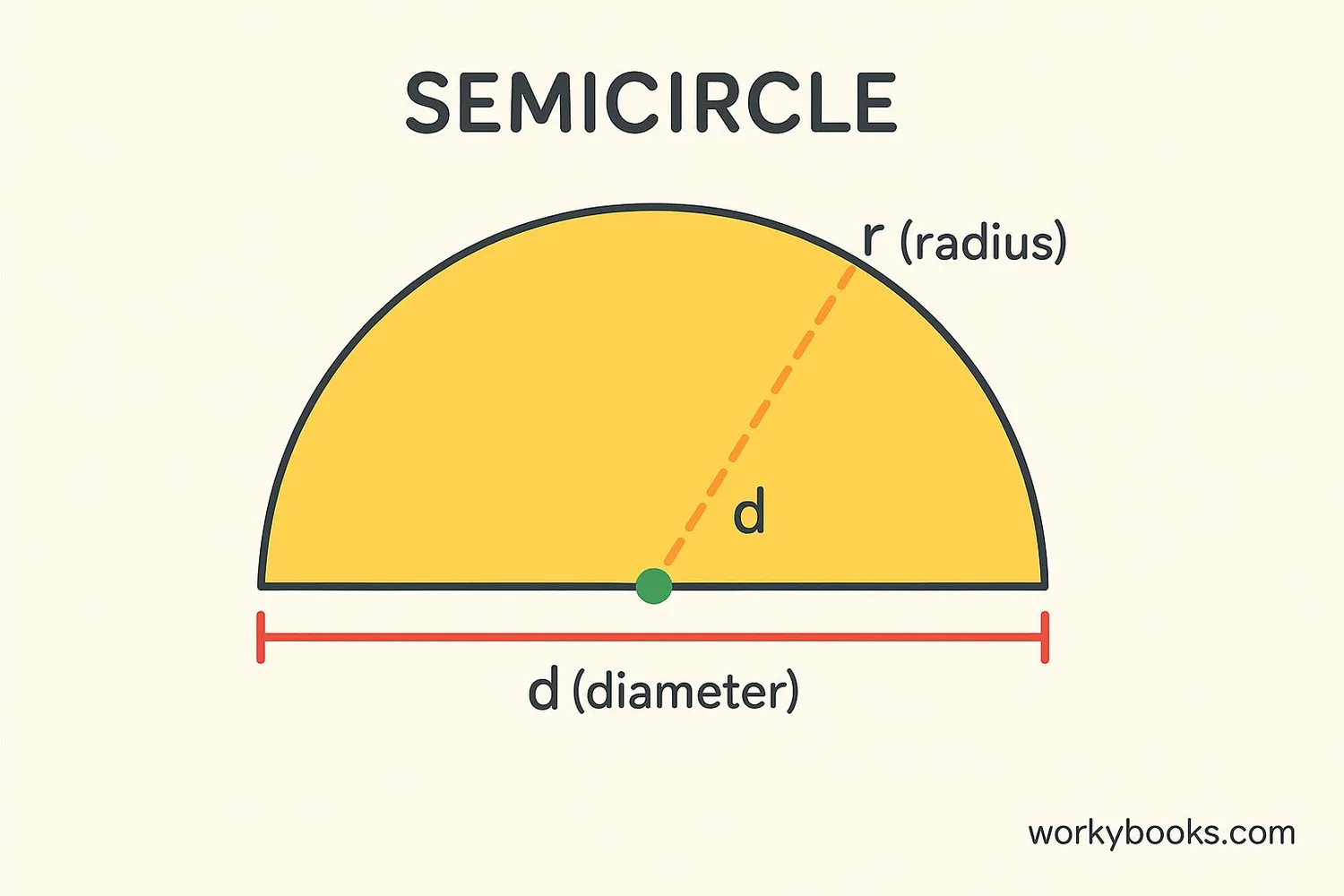
A semicircle is exactly half of a circle. It's formed by cutting a whole circle along its diameter. Imagine taking a round cookie and cutting it straight through the middle - each half is a semicircle!
The word "semi" means half, so "semicircle" literally means "half circle". Semicircles are all around us - in architecture (arches, windows), sports (basketball court markings), and everyday objects (protractors, half-moon shapes).
In mathematics, we study semicircles to understand:
- How to calculate their area
- How to find their perimeter (the distance around)
- How they relate to full circles
Key Concept
A semicircle has one curved edge (half the circumference of the original circle) and one straight edge (the diameter).
Area of a Semicircle Formula
To find the area of a semicircle, we start with the area of a full circle and divide it by 2. The area of a full circle is πr² (pi times radius squared), so:
Area Formula
Where π (pi) is approximately 3.14159 and r is the radius of the circle.
because the radius (r) is half the diameter (d), so r = d/2.
Let's practice with an example:Step 1: Area of full circle = π × (4)² = 3.14 × 16 = 50.24 cm²
Step 2: Area of semicircle = 50.24 ÷ 2 = 25.12 cm²
Using the formula: ½ × π × r² = ½ × 3.14 × 16 = 25.12 cm²
Real-World Examples
Let's practice with some real-world examples:
Solution: Area = ½ × π × r² = ½ × 3.14 × 49 = 76.93 m²
Solution: Radius = diameter ÷ 2 = 10 ÷ 2 = 5 m
Area = ½ × π × r² = ½ × 3.14 × 25 = 39.25 m²
Solution: Area = ½ × π × r²
1.57 = ½ × 3.14 × r²
1.57 = 1.57 × r²
r² = 1.57 ÷ 1.57 = 1
r = √1 = 1 meter
Remember
Always check if you're given the radius or diameter. The diameter is twice the radius!
Perimeter of a Semicircle
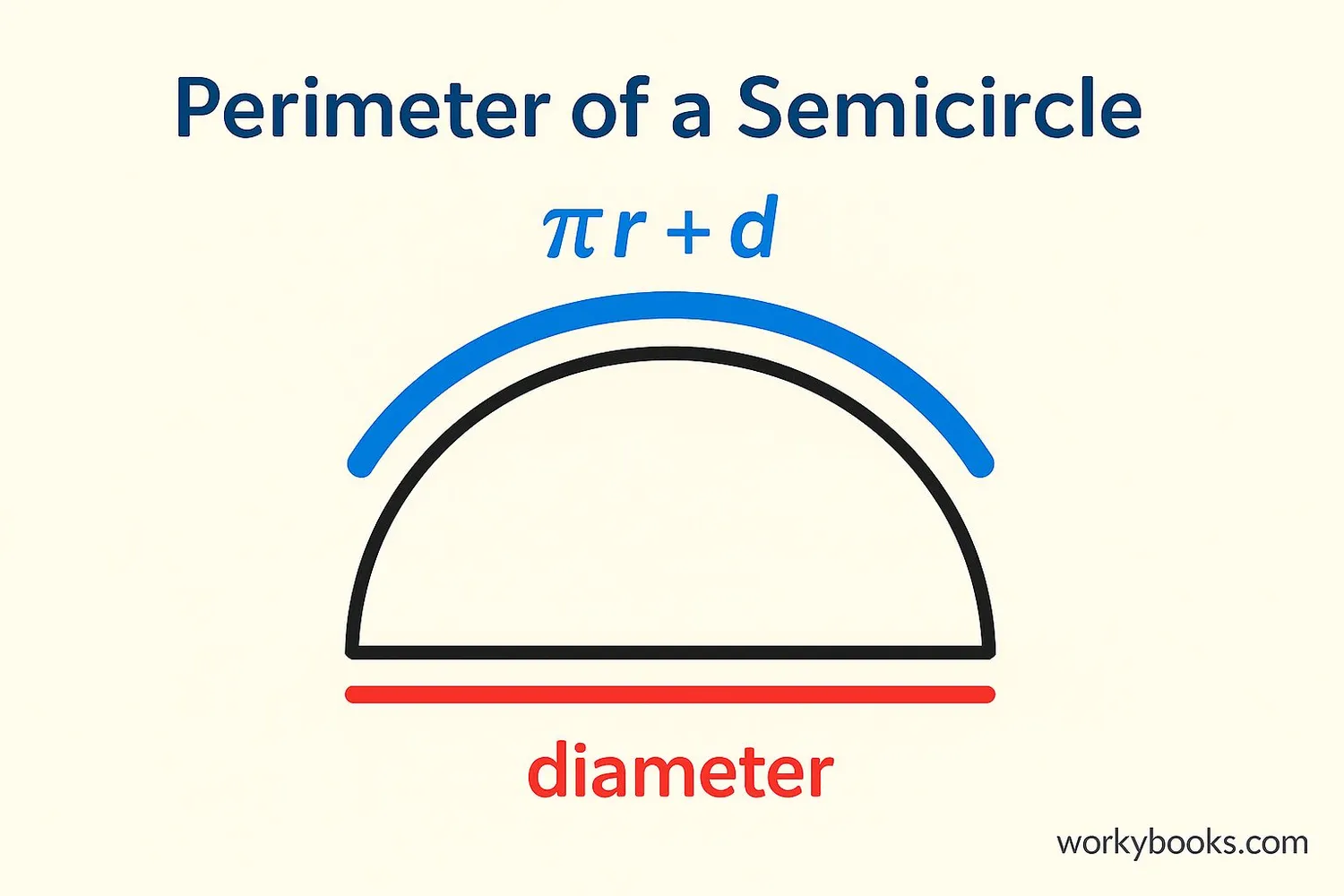
The perimeter of a semicircle is not simply half the perimeter of a circle because we also have to include the straight edge (the diameter).
The formula for the perimeter of a semicircle is:
Which we can also write as:
- πr is half the circumference of the full circle
- 2r is the diameter (since diameter = 2 × radius)
Solution:
Curved part = ½ × 2πr = πr = 3.14 × 5 = 15.7 cm
Straight part (diameter) = 2r = 2 × 5 = 10 cm
Total perimeter = 15.7 + 10 = 25.7 cm
Using the formula: r(π + 2) = 5 × (3.14 + 2) = 5 × 5.14 = 25.7 cm
Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about semicircles:
Math Trivia
Discover interesting facts about circles and semicircles:
Ancient Measurements
The ancient Egyptians were among the first to calculate the area of circles around 1800 BC. They used a value of π approximately equal to 3.16, which is remarkably close to today's value of 3.14159.
The Value of π
Mathematicians have calculated π to over 100 trillion decimal places! But for most calculations, we only need 3.14 or 22/7. The record was set in 2023 using a supercomputer.
Architectural Marvels
The Romans were masters of using semicircles in architecture. The Colosseum in Rome features multiple levels of semicircular arches, and the Pantheon has a massive semicircular dome that was the world's largest for over 1300 years.
Circle vs. Semicircle
Did you know that a semicircle has the largest area of any shape with the same perimeter? This property makes semicircular designs very efficient in nature and engineering.


