Area of an Equilateral Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate the area of equilateral triangles with simple explanations and practice activities
What is an Equilateral Triangle?
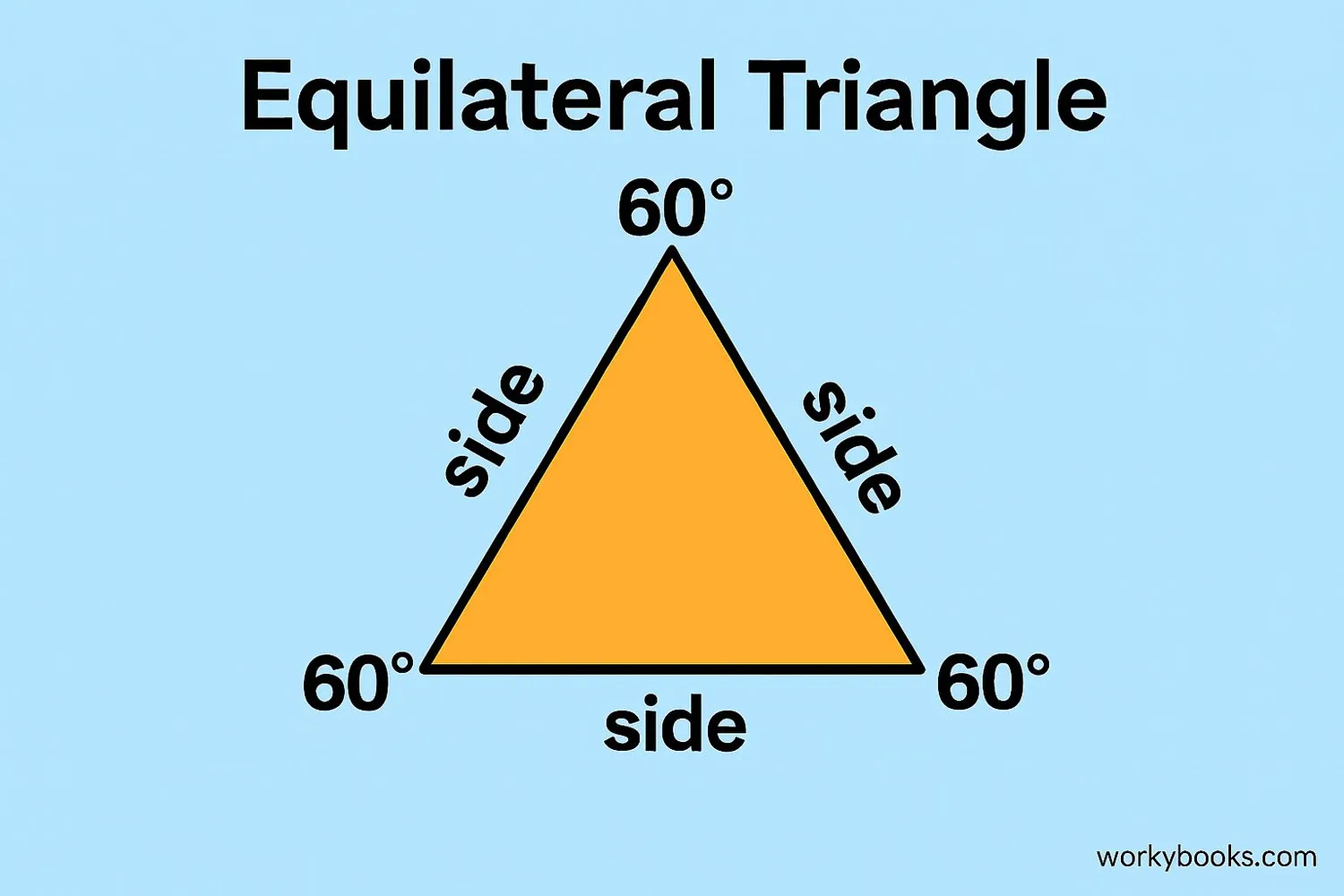
An equilateral triangle is a special type of triangle where all three sides are equal in length, and all three angles are equal to 60 degrees. The word "equilateral" comes from Latin: "equi" means equal, and "lateral" means sides.
Here are the key features:
- All three sides are the same length
- All three angles measure exactly 60 degrees
- It has three lines of symmetry
- It's a regular polygon with three sides
Equilateral triangles are found everywhere in our world - in architecture, art, and nature. Traffic signs, honeycombs, and some bridges use equilateral triangles because of their strength and balance.
Key Concept
All sides equal and all angles 60° - that's what makes a triangle equilateral!
Area Formula for Equilateral Triangles
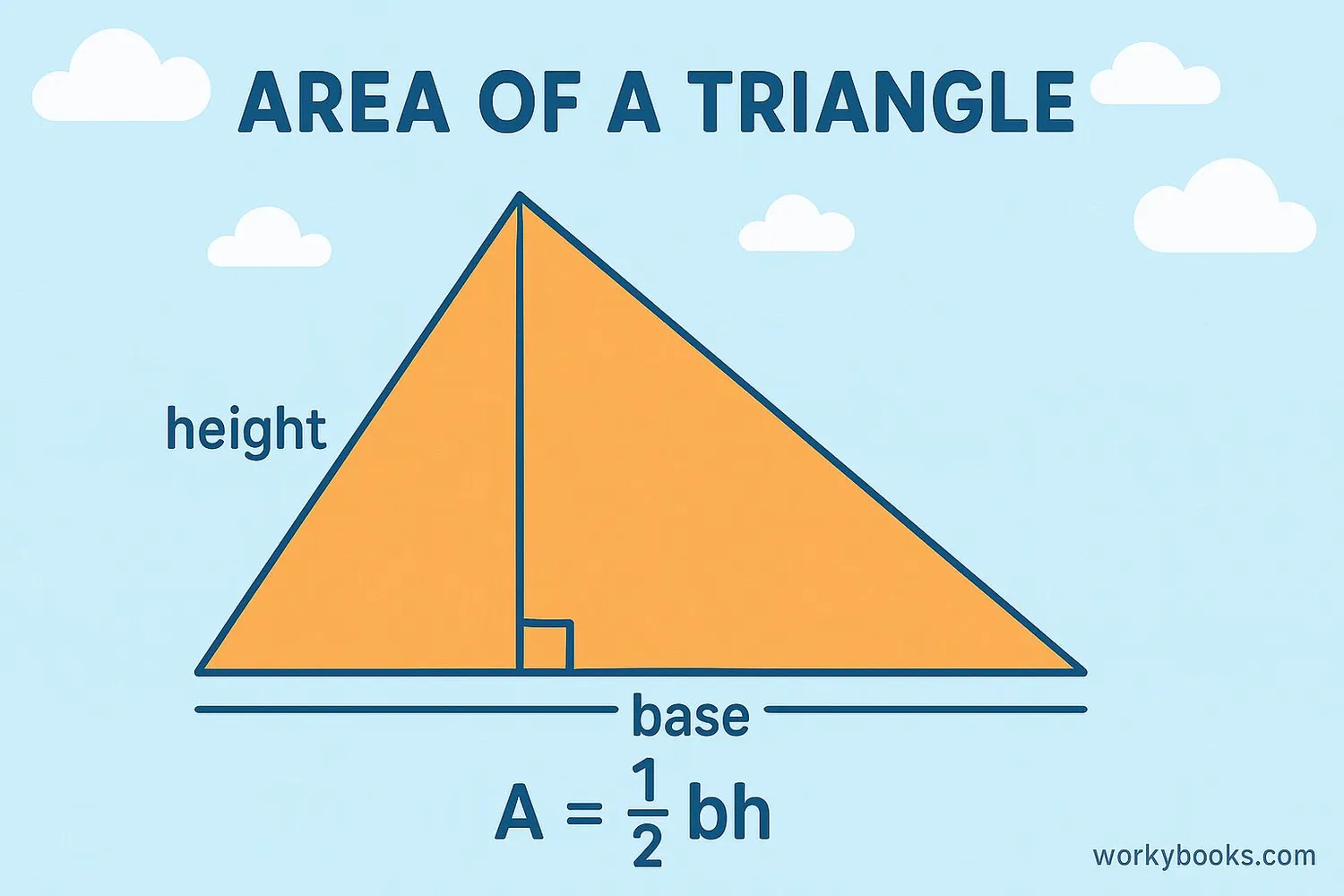
To find the area of any triangle, we usually use the formula: (base × height) ÷ 2. But for equilateral triangles, we have a special formula that only needs the length of one side!
Area Formula
Where "side" is the length of one side of the triangle
Why does this work? When we draw a height line in an equilateral triangle, it splits into two 30-60-90 right triangles. Using the properties of these special triangles, we can derive this formula.
Remember: This formula only works for equilateral triangles! For other triangles, you'll need to use the general area formula.
Remember
You only need to know the length of one side to calculate the area of an equilateral triangle!
Step-by-Step Examples
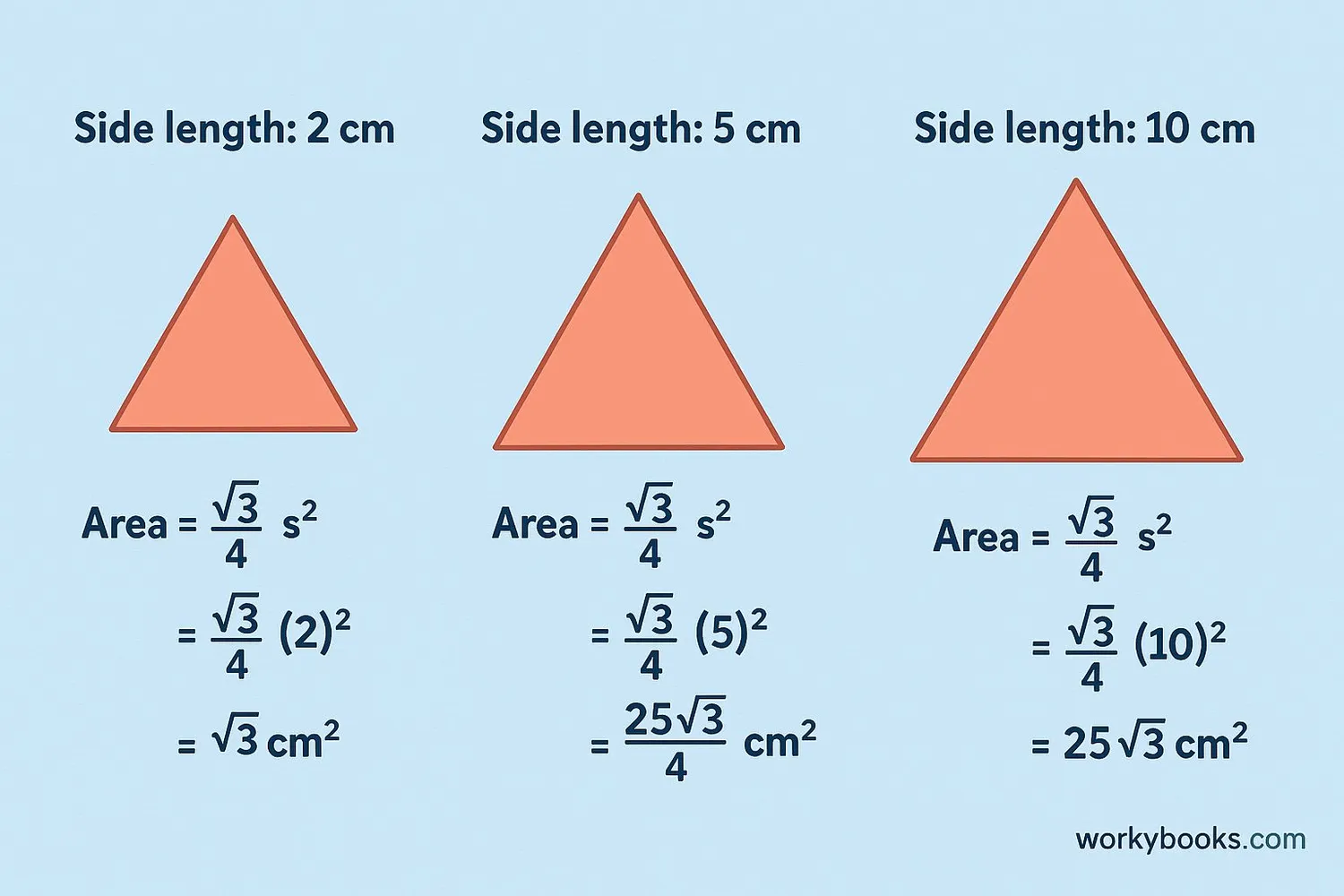
Let's practice calculating the area with some examples:
Example 1: Side length = 4 cm
Step 1: Write the formula: Area = (√3 ÷ 4) × side²
Step 2: Plug in the side length: (√3 ÷ 4) × (4)²
Step 3: Calculate: (1.732 ÷ 4) × 16 = (0.433) × 16
Step 4: Result: 6.928 cm²
Answer: Approximately 6.93 cm²
Example 2: Side length = 10 cm
Step 1: Formula: Area = (√3 ÷ 4) × side²
Step 2: Plug in: (√3 ÷ 4) × (10)²
Step 3: Calculate: (1.732 ÷ 4) × 100 = 0.433 × 100
Step 4: Result: 43.3 cm²
Answer: 43.3 cm²
Example 3: Side length = 6 m
Step 1: Formula: Area = (√3 ÷ 4) × side²
Step 2: Plug in: (√3 ÷ 4) × (6)²
Step 3: Calculate: (1.732 ÷ 4) × 36 = 0.433 × 36
Step 4: Result: 15.588 m²
Answer: Approximately 15.59 m²
Area Calculation Table
| Side Length | Area Calculation | Result |
|---|---|---|
| 2 cm | (√3 ÷ 4) × 4 | 1.732 cm² |
| 5 cm | (√3 ÷ 4) × 25 | 10.825 cm² |
| 8 cm | (√3 ÷ 4) × 64 | 27.712 cm² |
| 12 cm | (√3 ÷ 4) × 144 | 62.352 cm² |
Pattern Tip
Notice how when the side length doubles, the area becomes four times larger? This is because area depends on the square of the side length!
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about equilateral triangles:
Math Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The ancient Egyptians used triangles in pyramid construction over 4,500 years ago. The Great Pyramid of Giza has faces that are nearly equilateral triangles!
Nature's Triangles
Honeybees build honeycombs with hexagonal cells, but each hexagon is made of six equilateral triangles. This shape uses the least wax to hold the most honey!
Strong Shapes
Equilateral triangles are the strongest geometric shape for construction. That's why you see them in bridges, towers, and roof supports - they distribute weight evenly.
Art and Triangles
Many famous artists have used equilateral triangles in their work. Piet Mondrian and Wassily Kandinsky created abstract art based on geometric shapes including triangles.





