Area of Irregular Shapes - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate the area of composite shapes with easy methods and practice activities
What are Irregular Shapes?
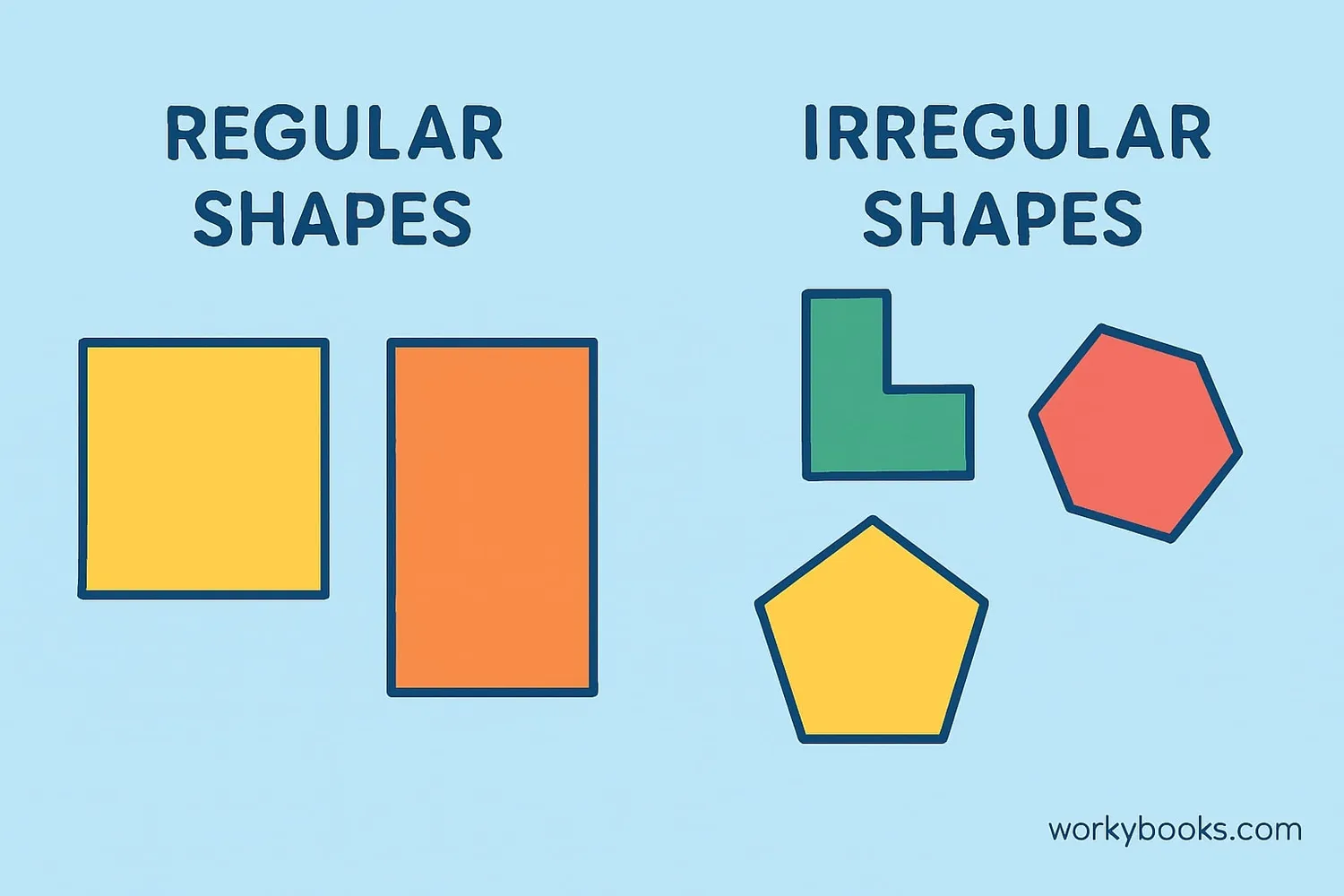
Irregular shapes, also called composite shapes, are shapes that don't have standard geometric forms like squares, rectangles, or circles. They might look like:
- A combination of different shapes put together (like a rectangle plus a triangle)
- Shapes with sides of different lengths and angles
- Objects we see in everyday life like lakes, playgrounds, or puzzle pieces
Finding the area of irregular shapes is like solving a puzzle! We break them into smaller regular shapes that we know how to measure, then combine those measurements.
Key Concept
Irregular shapes can be decomposed (broken down) into regular shapes whose areas we can calculate using standard formulas.
How to Find the Area of Irregular Shapes
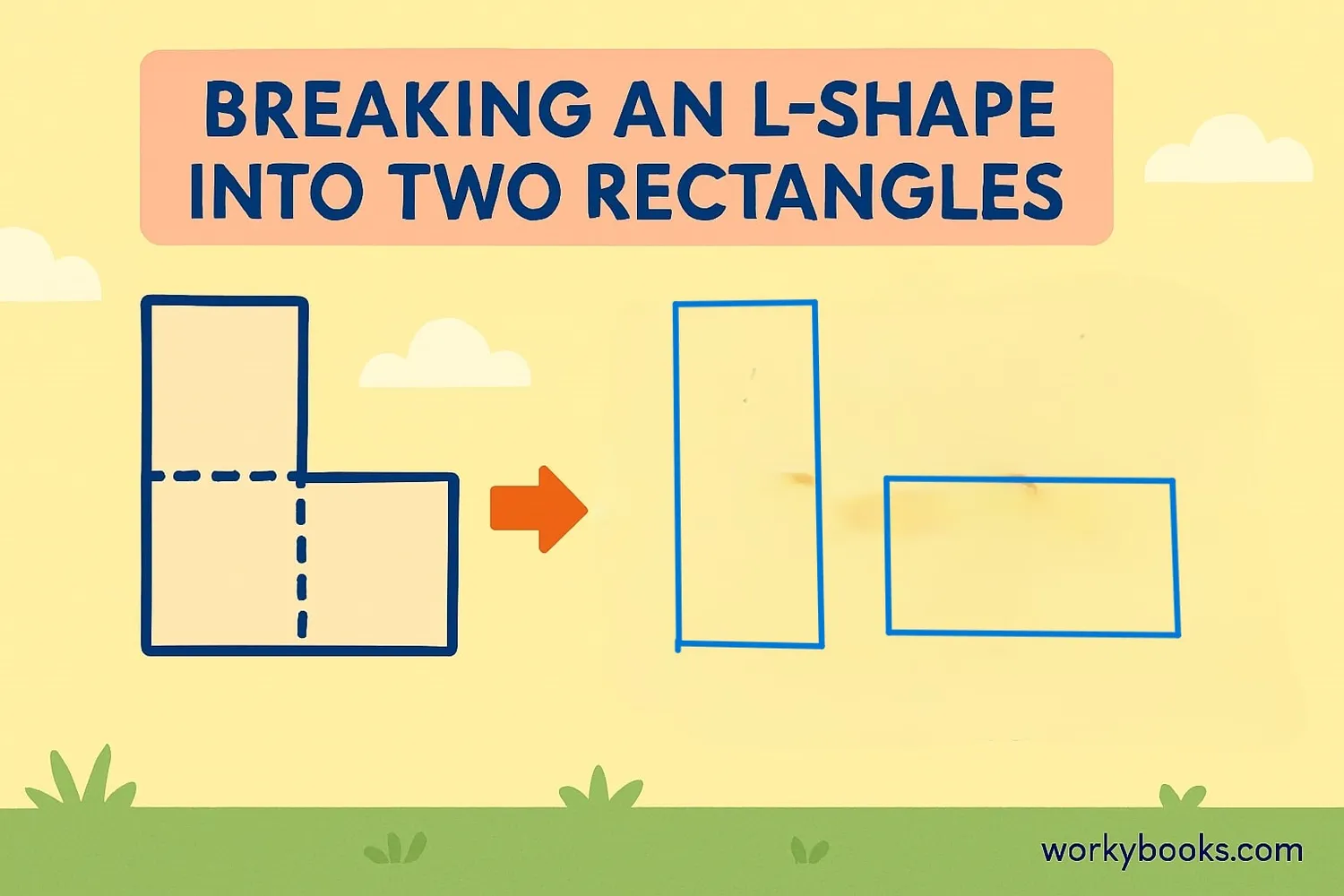
There are two main methods to find the area of irregular shapes:
Decomposition Method
Break the irregular shape into smaller regular shapes (rectangles, triangles, circles, etc.). Calculate each area separately, then add them together.
Subtraction Method
Draw a regular shape around the irregular shape. Calculate the area of the regular shape, then subtract the areas of the extra parts.
Important Formulas
Area of Rectangle = length × width
Area of Triangle = ½ × base × height
Area of Circle = π × radius²
Remember
Always use the same units of measurement throughout your calculations. If measurements are in centimeters, your area will be in square centimeters (cm²).
Real-World Examples
Example 1: L-Shape
An L-shaped room has two rectangles: 8m × 4m and 4m × 4m.
Area = (8 × 4) + (4 × 4) = 32 + 16 = 48 m²
Example 2: House Shape
A house-shaped figure: triangle on top of a rectangle. Rectangle: 10m × 6m. Triangle: base 10m, height 4m.
Area = (10 × 6) + (½ × 10 × 4) = 60 + 20 = 80 m²
Example 3: Subtraction Method
A rectangle with a semicircle removed: Rectangle 12cm × 8cm. Semicircle diameter 8cm.
Area = (12 × 8) - (½ × π × 4²) ≈ 96 - 25.13 = 70.87 cm²
Practice Tip
Draw dotted lines to show how you're breaking down the shape. This helps you keep track of which parts you're measuring.
Area Calculation Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about calculating the area of irregular shapes:
Measurement Trivia
Discover interesting facts about area and measurement:
Ancient Area Measurement
The ancient Egyptians were among the first to develop area measurement techniques to restore field boundaries after Nile River floods, using ropes and geometry.
Largest Irregular Shape
The Great Lakes in North America form one of the world's largest irregular shapes, with a combined surface area of about 244,000 square kilometers.
Fractal Areas
Some irregular shapes called fractals have finite area but infinite perimeter! The Koch snowflake is a famous example where the area is limited but the boundary goes on forever.
Irregular in Nature
Most shapes in nature are irregular - clouds, coastlines, and leaves are all examples where calculating area requires special methods.


