Area of a Parallelogram - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate the area of parallelograms with easy formulas and step-by-step examples
What is the Area of a Parallelogram?
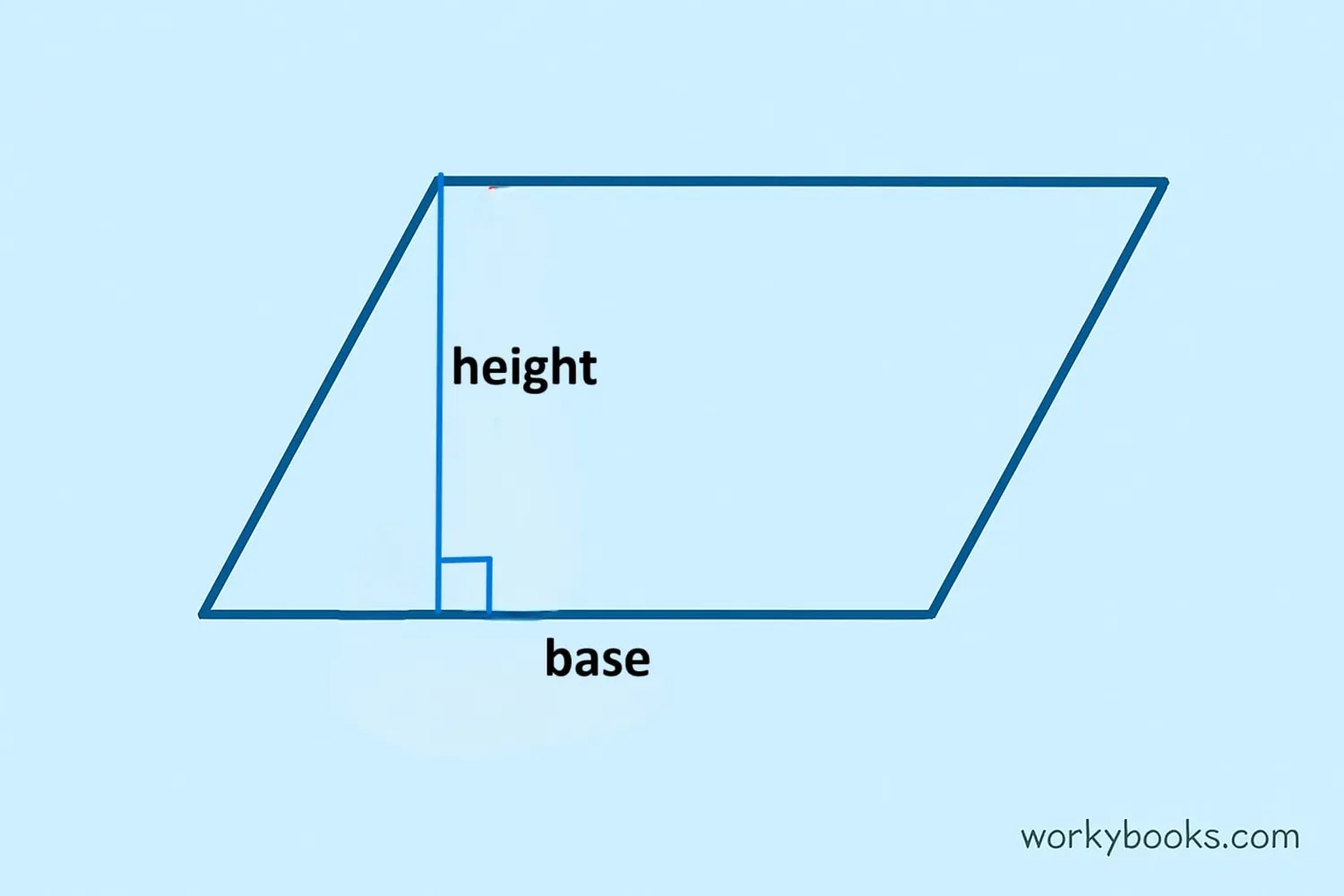
A parallelogram is a special quadrilateral with two pairs of parallel sides. The area of a parallelogram is the amount of space inside its boundaries. It's measured in square units like cm², m², or ft².
Every parallelogram has:
- Base - any one of its sides (we usually use the bottom side)
- Height - the perpendicular distance between the base and its opposite side
The area of a parallelogram is calculated by multiplying the base by the height. This is similar to the area formula for a rectangle, because any parallelogram can be rearranged to form a rectangle without changing its area.
Key Concept
The height must be perpendicular to the base. The slanted side is not the height!
How to Calculate the Area
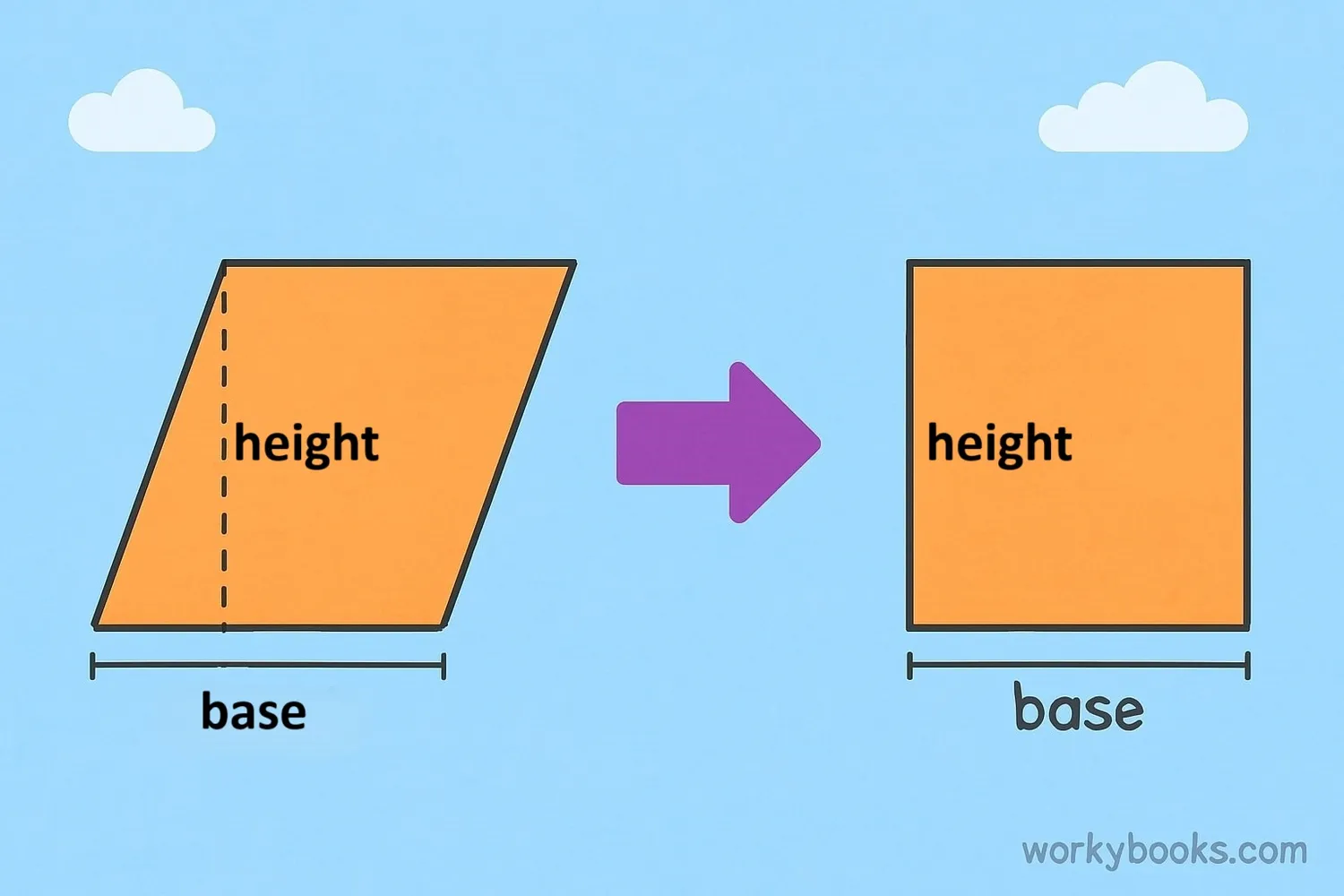
The formula for calculating the area of a parallelogram is simple:
Area Formula
Multiply the base length by the height (the perpendicular height)
- Identify the base (b) of the parallelogram
- Find the height (h) - the perpendicular distance to the opposite side
- Multiply base times height: A = b × h
- Include square units in your answer
Remember
The height is always perpendicular to the base. It's not the length of the slanted side!
Solved Examples
Example 1
Problem: Find the area of a parallelogram with base 8 cm and height 5 cm.
Solution: A = b × h = 8 × 5 = 40 cm²
Example 2
Problem: A parallelogram has base 10 m and height 7 m. What is its area?
Solution: A = b × h = 10 × 7 = 70 m²
Example 3
Problem: Calculate the area of a parallelogram where base is 12 ft and height is 4 ft.
Solution: A = 12 × 4 = 48 ft²
Example 4
Problem: A parallelogram-shaped garden has base 15 cm and height 6 cm. Find its area.
Solution: A = 15 × 6 = 90 cm²
Real-World Connection
Parallelograms are everywhere! Floor tiles, solar panels, and even some buildings use parallelogram shapes. Understanding area helps architects and designers create efficient spaces.
Practice Quiz
Test your understanding with these practice questions. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about parallelograms:
Math Trivia
Discover interesting facts about parallelograms and geometry:
Ancient Origins
The concept of area calculation dates back to ancient Egypt around 1850 BC. Egyptian surveyors called "rope-stretchers" used geometry to re-establish field boundaries after Nile River floods.
Crystal Structures
Parallelograms appear in crystal structures. Many minerals form parallelogram-shaped faces because of their molecular arrangement. This property helps geologists identify minerals.
Structural Strength
Parallelogram shapes are used in truss bridges and roof supports because they distribute weight efficiently. This geometric shape provides excellent structural stability in construction.
Artistic Patterns
Parallelograms are fundamental in tessellations and Islamic geometric art. Artists like M.C. Escher used parallelogram grids to create his famous mathematical artwork.


