Area of Shapes - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate area for different 2D shapes with easy explanations and practice activities
What is Area?
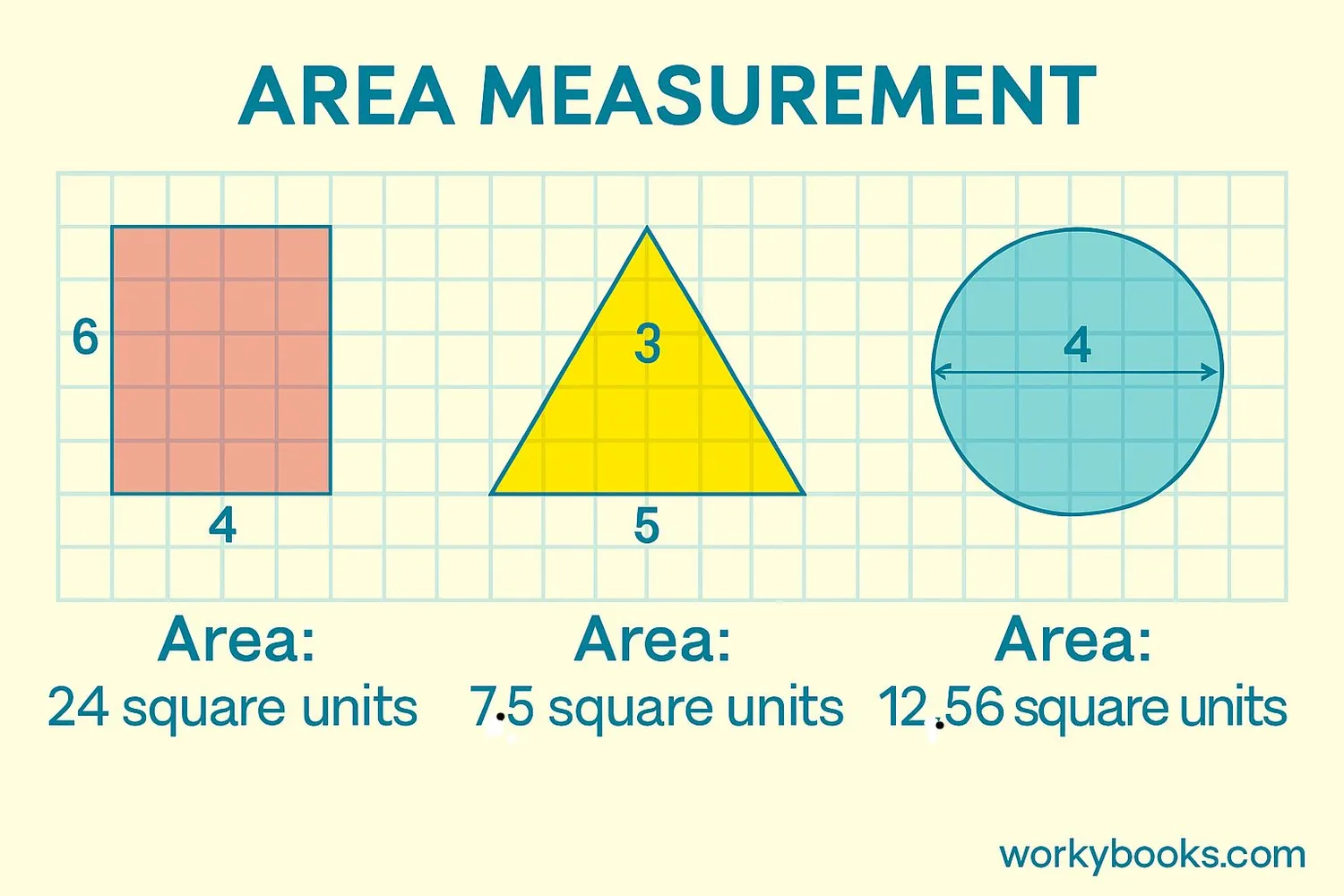
Area is the amount of space inside a 2D shape. Think of it like how much paint you would need to cover a surface. Area is measured in square units like square centimeters (cm²) or square meters (m²).
Why is area important? We use area measurements in everyday life - for painting walls, laying carpet, planting gardens, and much more. Understanding area helps us solve real-world problems efficiently.
Area is different from perimeter. Perimeter is the distance around a shape, while area is the space inside it. A shape with a large perimeter might have a small area, and vice versa.
Key Concept
Area measures the space inside a shape. It's always expressed in square units.
How to Calculate Area
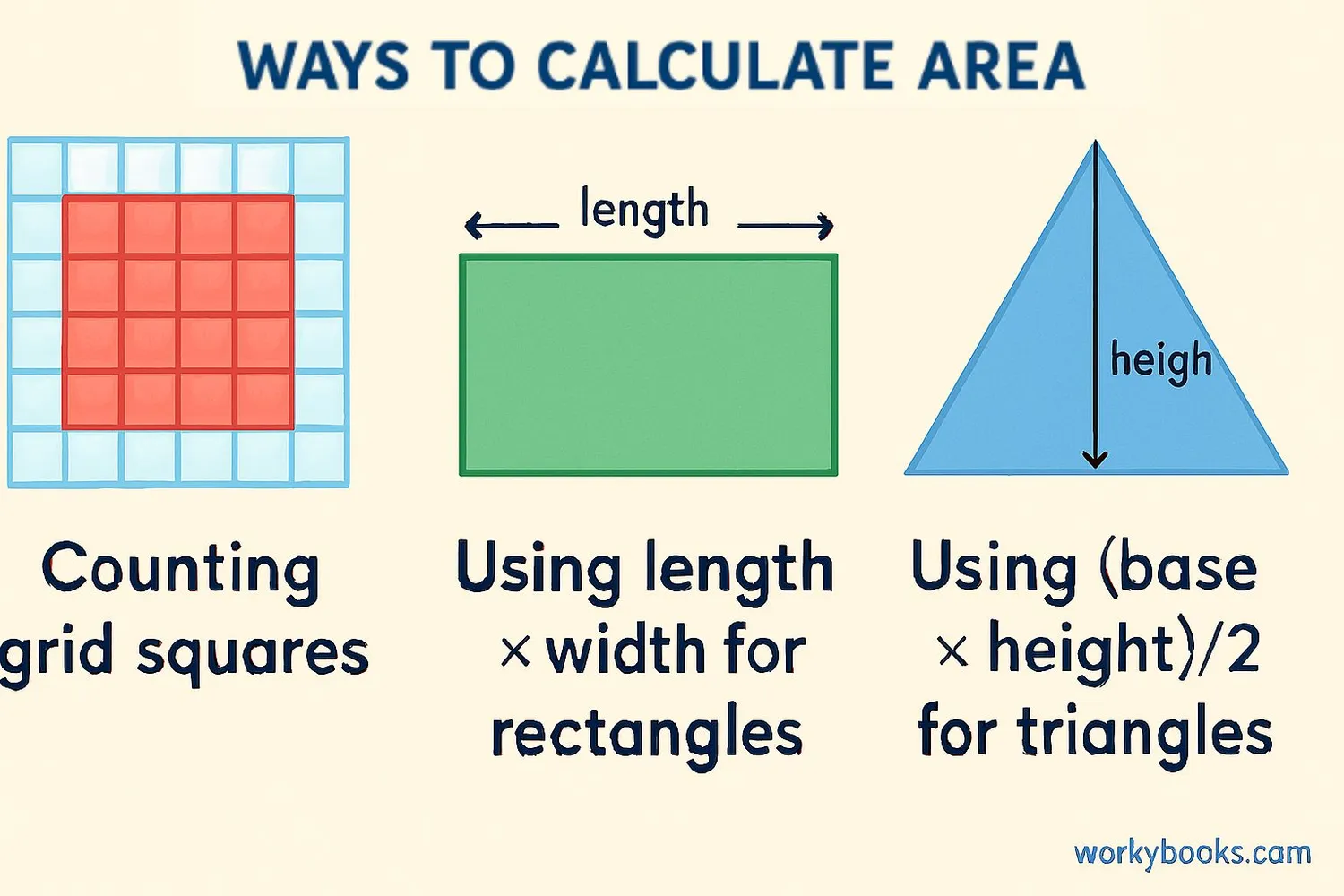
There are different ways to calculate area depending on the shape:
1. Counting squares: For simple shapes, you can count the number of unit squares that fit inside the shape. This is a great way to understand what area means.
2. Using formulas: For common shapes, we have special formulas that make area calculation quick and easy. These formulas are based on the shape's dimensions.
3. Breaking into parts: For complex shapes, you can break them into simpler shapes, calculate each area, then add them together.
The basic formula for rectangles is:
Rectangle Area Formula
For any rectangle, multiply its length by its width to find the area.
Remember
Always include units when measuring area. If measurements are in centimeters, area will be in square centimeters (cm²).
Area Formulas for Common Shapes
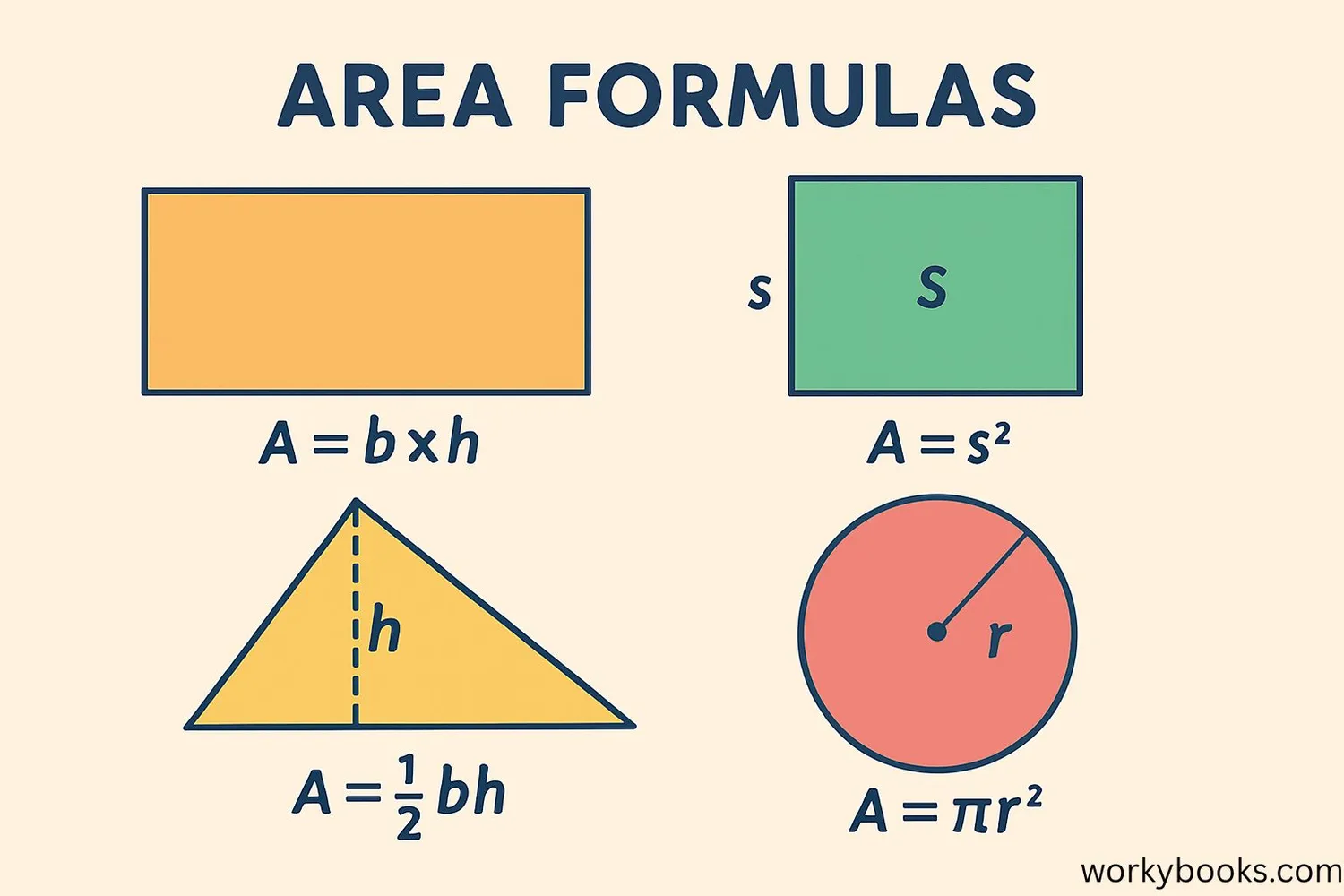
Different shapes have different area formulas. Here are the most important ones to remember:
| Shape | Formula | Description |
|---|---|---|
| Square | A = s² | Side length squared |
| Rectangle | A = l × w | Length times width |
| Triangle | A = ½ × b × h | Half base times height |
| Circle | A = πr² | Pi times radius squared |
| Parallelogram | A = b × h | Base times height |
| Trapezoid | A = ½(a+b)h | Half the sum of parallel sides times height |
Remember
For triangles, height is always perpendicular to the base. Make sure you're using the correct height measurement.
Real-World Examples
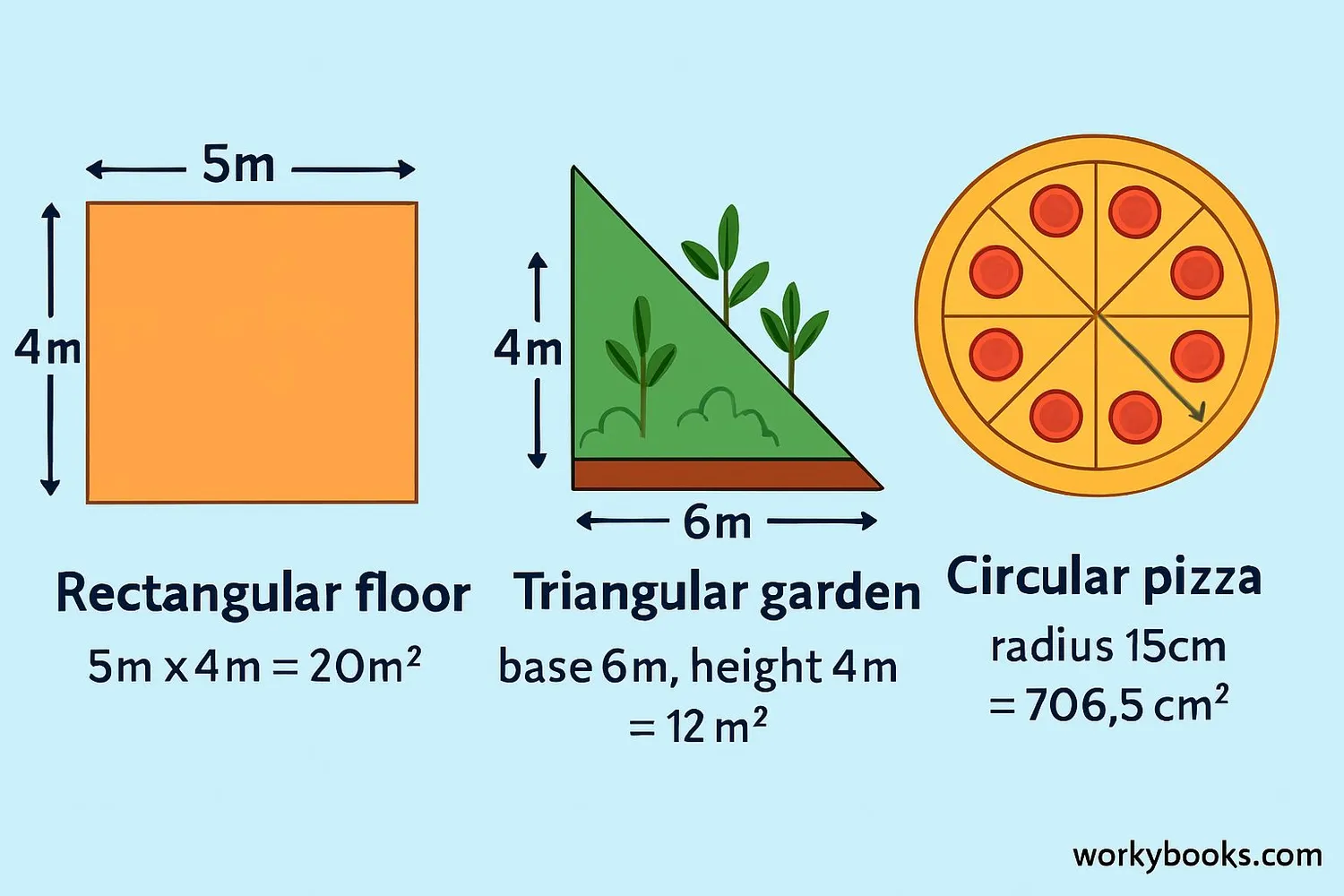
Let's practice area calculation with some real-world examples:
Example 1: A rectangular classroom floor is 8 meters long and 6 meters wide. What is its area?
Solution: Area = length × width = 8m × 6m = 48m²
Example 2: A triangular garden has a base of 5 meters and height of 3 meters. What area can be planted?
Solution: Area = ½ × base × height = 0.5 × 5m × 3m = 7.5m²
Example 3: A square tile has sides of 30 centimeters. What is its area?
Solution: Area = side × side = 30cm × 30cm = 900cm²
Example 4: A circular pizza has a radius of 15cm. What is its area?
Solution: Area = π × radius² ≈ 3.14 × (15cm)² = 3.14 × 225 = 706.5cm²
Practice calculating areas of objects around you - your notebook, a window, or your bedroom floor!
Measurement Tip
When solving area problems, always check that your measurements are in the same units before calculating.
Area Calculation Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about area calculation:
Area and Measurement Trivia
Discover interesting facts about area and measurement:
Ancient Area Measurement
The ancient Egyptians developed geometry to measure farmland areas after Nile River floods. Their "rope stretchers" measured fields using knotted ropes to calculate areas for taxation.
Largest Country by Area
Russia is the largest country by area, covering about 17.1 million square kilometers. That's about 11% of the world's landmass! The smallest country is Vatican City at just 0.44 km².
Area in Space
The largest known structure in the universe is the Hercules-Corona Borealis Great Wall, a galaxy supercluster measuring approximately 10 billion light-years in area. That's about 10% of the observable universe!
Largest Man-Made Structure
The Great Wall of China has the largest surface area of any man-made structure. If you could lay it flat, it would cover approximately 7,200,000 m² - about the area of 1,000 football fields!


