Area of Triangle in Determinant Form - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate triangle area using coordinates and determinants
What is the Area of a Triangle in Determinant Form?
The determinant form is a special way to find the area of a triangle when we know the coordinates of its three vertices (corners). Instead of using the base and height, we use the coordinates to calculate the area.
This method is especially useful in coordinate geometry, where we have points on a grid. The formula might look complicated at first, but it's like following a recipe - once you know the steps, it's easy!
The key idea is that the area of a triangle can be calculated using the coordinates of its vertices (x₁,y₁), (x₂,y₂), and (x₃,y₃) with this formula:
Area Formula
The vertical bars | | mean we take the absolute value (positive number)
Key Concept
The determinant formula gives us the area of a triangle directly from its coordinates without needing to know the base or height!
How to Calculate Area with Determinants

Let's break down the formula into simple steps:
1. Identify the coordinates of the three vertices: (x₁,y₁), (x₂,y₂), (x₃,y₃)
2. Calculate: (x₁ × (y₂ - y₃))
3. Calculate: (x₂ × (y₃ - y₁))
4. Calculate: (x₃ × (y₁ - y₂))
5. Add these three results together
6. Take the absolute value (positive number) of this sum
7. Divide by 2
We can also represent this using a matrix determinant:
The area is half the absolute value of this determinant
Remember
The order of the vertices matters! Always list them in either clockwise or counterclockwise order.
Step-by-Step Examples
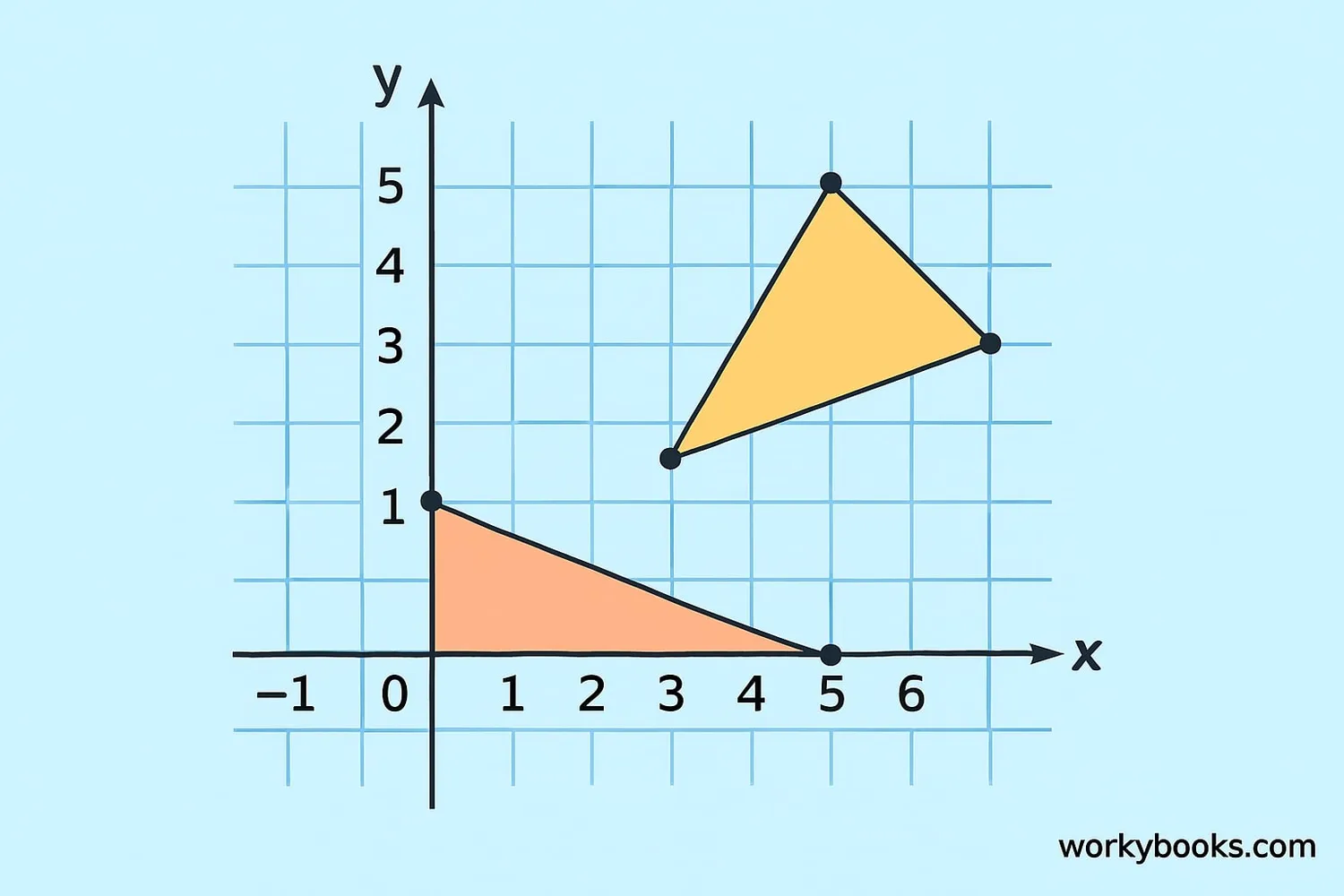
Let's work through some examples to see how the formula works:
Example 1: Triangle with vertices at (0,0), (4,0), and (0,3)
Step 1: Identify coordinates: (x₁,y₁) = (0,0), (x₂,y₂) = (4,0), (x₃,y₃) = (0,3)
Step 2: Apply the formula:
(0×(0 - 3)) + (4×(3 - 0)) + (0×(0 - 0)) = (0×-3) + (4×3) + (0×0) = 0 + 12 + 0 = 12
Step 3: Take absolute value: |12| = 12
Step 4: Divide by 2: 12 ÷ 2 = 6
Area = 6 square units
Example 2: Triangle with vertices at (1,1), (4,2), (2,5)
Step 1: (x₁,y₁) = (1,1), (x₂,y₂) = (4,2), (x₃,y₃) = (2,5)
Step 2: (1×(2 - 5)) + (4×(5 - 1)) + (2×(1 - 2)) = (1×-3) + (4×4) + (2×-1) = -3 + 16 - 2 = 11
Step 3: |11| = 11
Step 4: 11 ÷ 2 = 5.5
Area = 5.5 square units
Practice Tip
Try drawing the triangle on graph paper to verify your calculation!
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about triangle areas:
Math Trivia
Discover interesting facts about geometry and determinants:
Historical Origins
Determinants were first studied by Japanese mathematician Seki Takakazu in 1683 and independently by German mathematician Gottfried Leibniz in 1693.
Beyond Triangles
The determinant method can be extended to find areas of polygons with more sides by dividing them into triangles!
Real-World Applications
Computer graphics programs use determinant formulas to calculate areas and transformations when rendering 3D objects on screens.
Matrix Power
Determinants are used in many areas of mathematics including solving systems of equations, finding inverses of matrices, and in vector calculus.





