Ascending Order - Definition, Examples, Quiz, FAQ, Trivia
Learn to arrange numbers from smallest to largest with step-by-step examples and practice activities
What is Ascending Order?

Ascending order means arranging numbers or items from the smallest to the largest.
It's like climbing stairs - you start at the bottom (smallest number) and go up to the top (largest number).
For example, if you have the numbers 3, 1, and 4, you would arrange them as 1, 3, 4.
We call this "ascending order" because the numbers ascend (go up) from smallest to largest.
Ascending order is important in math because it helps us organize information, find patterns,
and solve problems more easily. It's a fundamental skill you'll use throughout your math learning!
Key Concept
Ascending order = from smallest to largest. Think of it as going up a staircase!
Simple Example
These numbers are arranged in ascending order because each number is larger than the one before it.
How to Arrange Numbers in Ascending Order
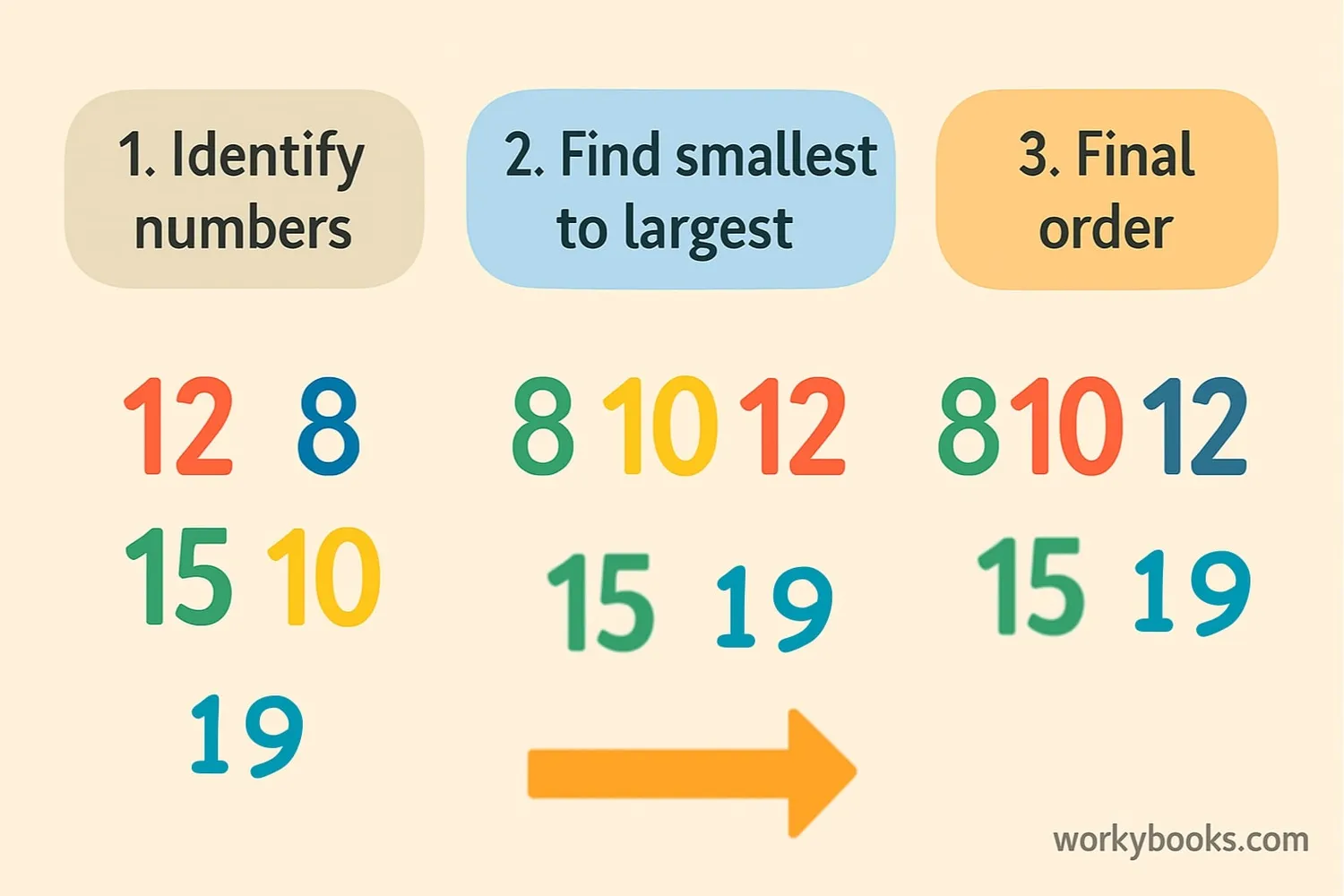
Arranging numbers in ascending order is easy when you follow these steps:
1. Identify all the numbers you need to arrange.
2. Find the smallest number in the group.
3. Write that number first.
4. Find the next smallest number from the remaining numbers.
5. Continue until all numbers are arranged from smallest to largest.
Let's practice with an example:
Example: Arrange 8, 3, 6, 1 in ascending order
Step 1: Numbers are 8, 3, 6, 1
Step 2: Smallest is 1 → Write 1
Step 3: Next smallest is 3 → Write 3
Step 4: Next smallest is 6 → Write 6
Step 5: Last number is 8 → Write 8
Final order: 1, 3, 6, 8
Remember
When arranging numbers, always start by finding the smallest number first, then work your way up to the largest.
Ascending Order with Integers
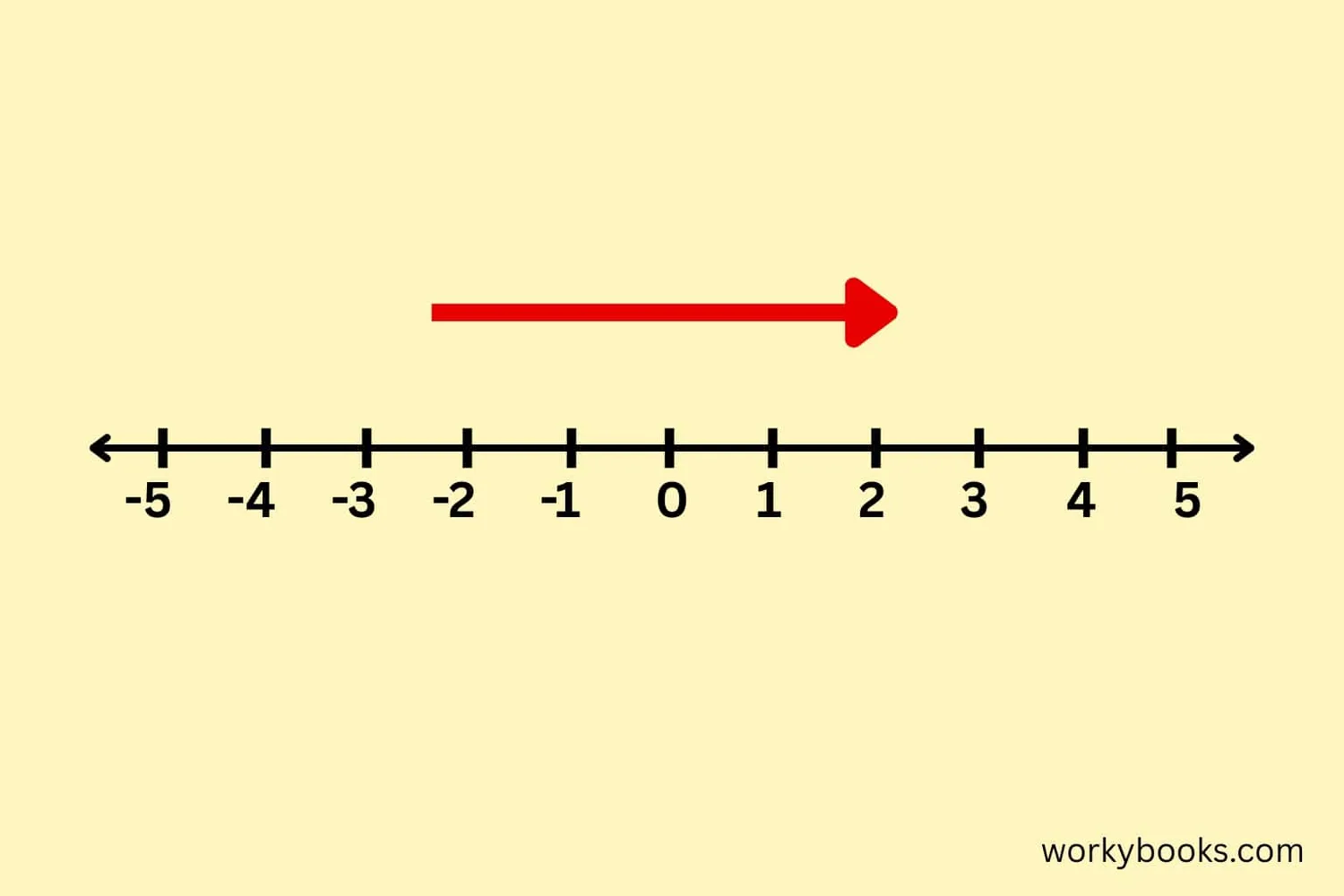
Integers include both positive and negative numbers, along with zero.
Arranging integers in ascending order follows the same rules but includes negative numbers.
Remember that negative numbers are smaller than positive numbers.
The further left a number is on the number line, the smaller it is.
Key points:
- Negative numbers are smaller than zero
- Positive numbers are larger than zero
- Among negative numbers, larger numbers are actually smaller (e.g., -3 is larger than -5)
Example: Arrange -3, 5, 0, -1, 2 in ascending order
Step 1: The smallest number is -3
Step 2: Next smallest is -1
Step 3: Then 0
Step 4: Then 2
Step 5: Then 5
Final order: -3, -1, 0, 2, 5
Number Line Tip
Imagine numbers on a number line - ascending order always goes from left to right.
Ascending Order with Fractions
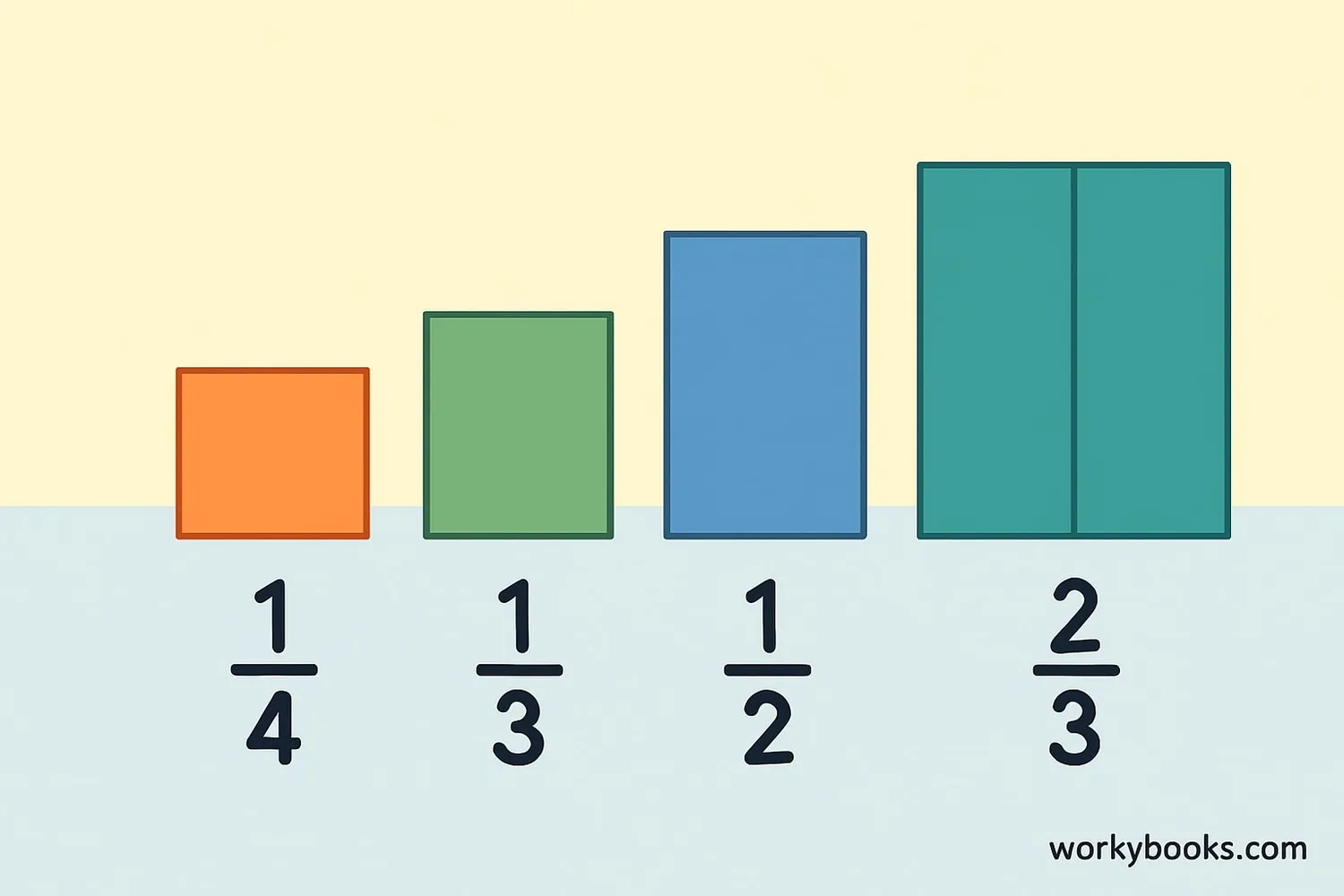
Arranging fractions in ascending order can be tricky because fractions have different denominators.
Here's how to do it:
1. Find a common denominator for all the fractions
2. Convert all fractions to equivalent fractions with this common denominator
3. Compare the numerators of the new fractions
4. Arrange them based on the numerators from smallest to largest
Example: Arrange 1/2, 1/3, 3/4 in ascending order
Step 1: Common denominator for 2, 3, 4 is 12
Step 2: Convert fractions:
1/2 = 6/12
1/3 = 4/12
3/4 = 9/12
Step 3: Compare numerators: 4, 6, 9
Step 4: Ascending order: 4/12, 6/12, 9/12 → 1/3, 1/2, 3/4
Fraction Tip
When denominators are the same, the fraction with the smaller numerator is smaller.
Ascending Order with Decimals
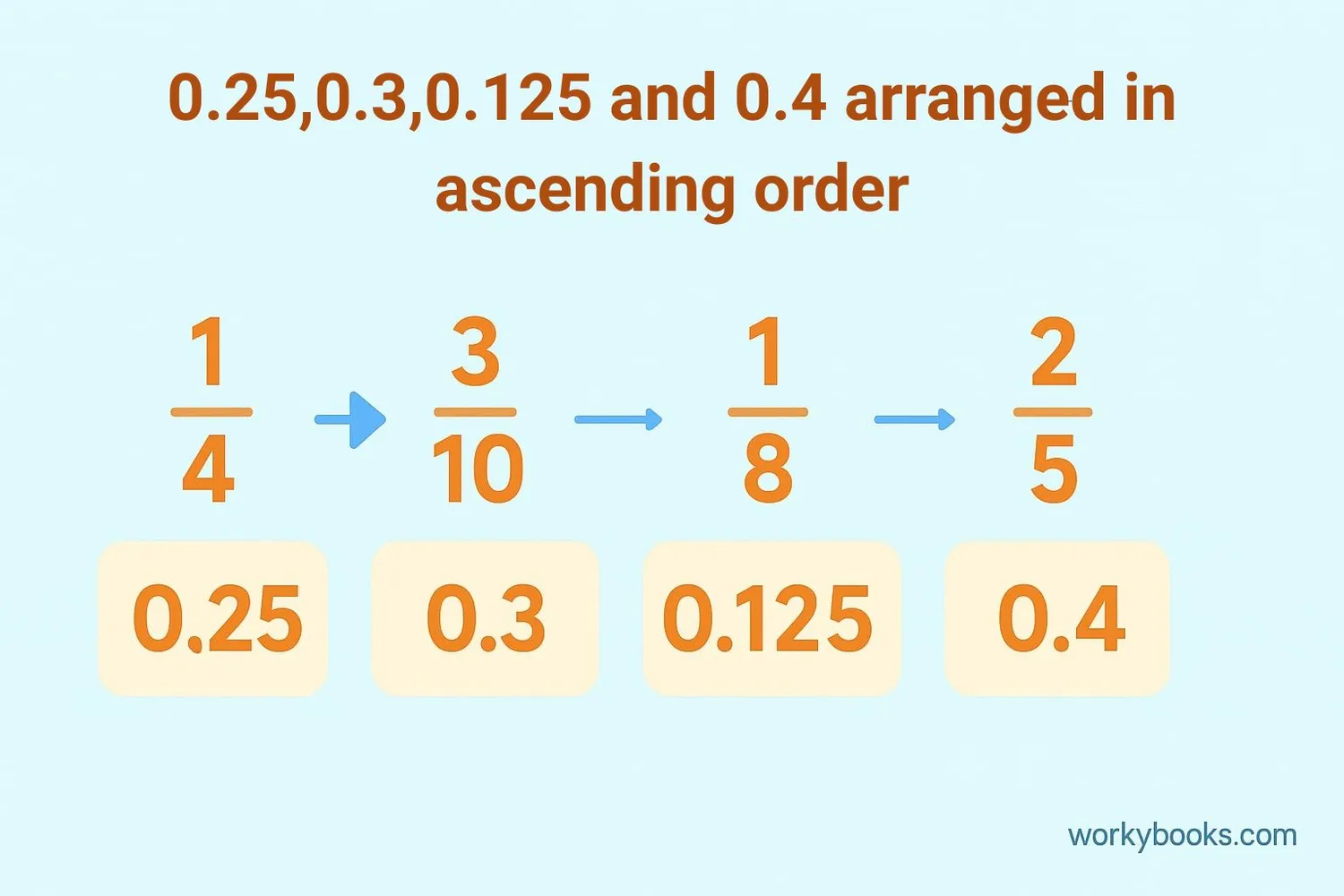
Arranging decimals in ascending order is similar to whole numbers but requires attention to place values.
Steps:
1. Compare the whole number part (to the left of the decimal point)
2. If whole numbers are the same, compare the tenths place
3. If tenths are the same, compare the hundredths place
4. Continue until all decimals are compared
Example: Arrange 2.3, 1.75, 2.15, 1.8 in ascending order
Step 1: Compare whole numbers - 1.75 and 1.8 have smaller whole numbers
Step 2: Between 1.75 and 1.8: 1.75 = 1.75, 1.8 = 1.80 → 1.75 < 1.80
Step 3: Between 2.3 and 2.15: 2.15 < 2.30
Final order: 1.75, 1.8, 2.15, 2.3
Decimal Tip
Add trailing zeros to make decimals easier to compare: 1.8 = 1.80, 2.3 = 2.30
Ascending Order Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about ascending order:
Math Trivia
Discover interesting facts about numbers and ordering:
Ancient Number Systems
The concept of ordering numbers dates back to ancient civilizations. The Egyptians had hieroglyphs for numbers as early as 3000 BC and understood the concept of numerical order.
Infinite Numbers
There are infinitely many numbers between any two numbers! For example, between 1 and 2, there are numbers like 1.1, 1.11, 1.111, and so on forever.
Largest Number
The largest named number is a "googolplex" - that's 1 followed by a googol of zeros! A googol is 1 followed by 100 zeros. We can't even write out a googolplex because there isn't enough space in the universe!
Computer Sorting
Computers use special algorithms to sort data. The fastest sorting algorithms can arrange millions of numbers in seconds! Some common sorting algorithms are called Bubble Sort, Quick Sort, and Merge Sort.





