Associative Property of Addition - Definition, Examples, Quiz, FAQ, Trivia
Learn how numbers can be grouped differently in addition problems with easy explanations and practice activities
What is the Associative Property of Addition?
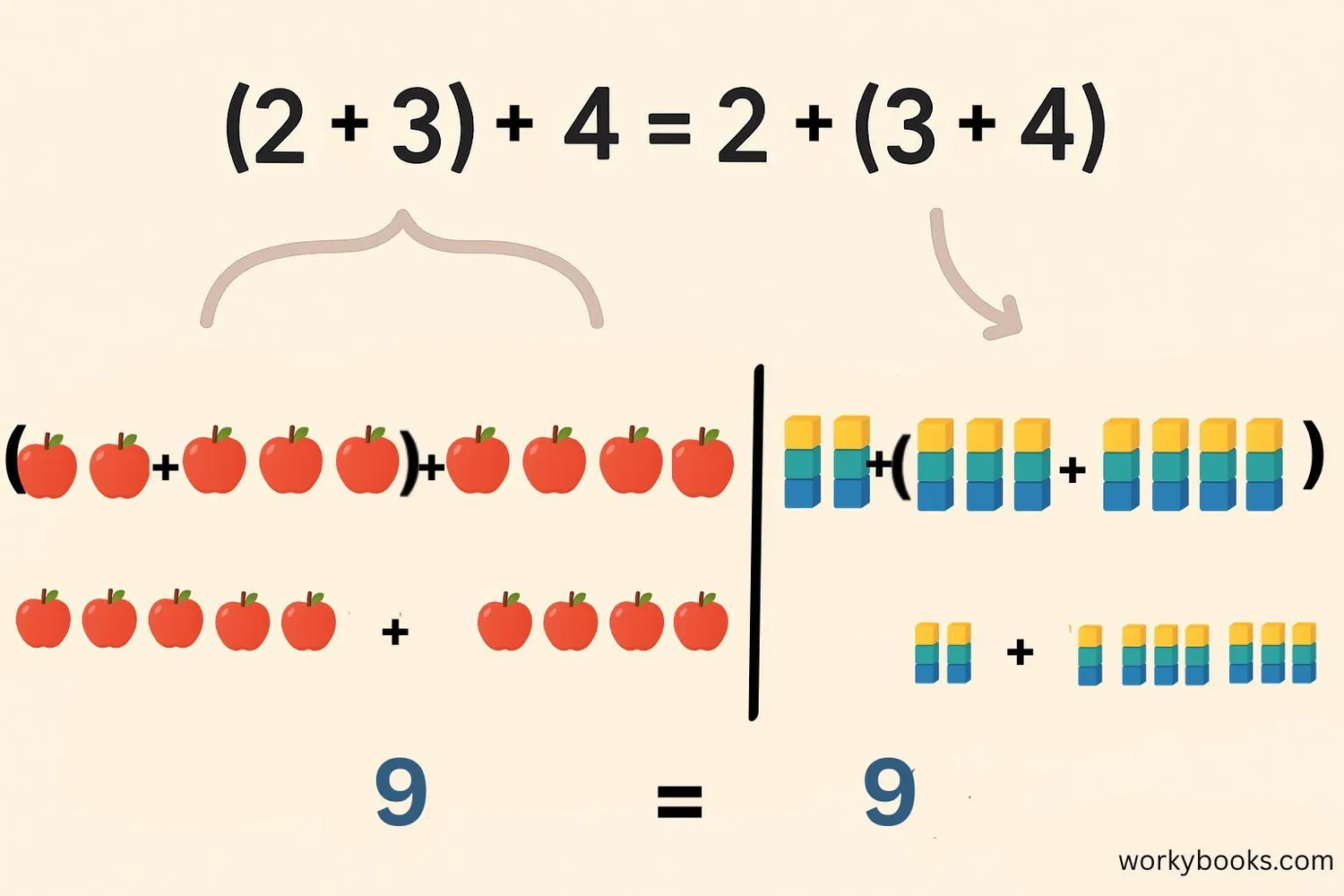
The associative property of addition tells us that how we group numbers when adding doesn't change the sum.
This means that when we add three or more numbers together, it doesn't matter which numbers we add first - the total will always be the same.
The mathematical way to say this is:
Associative Property Formula
Where a, b, and c are any numbers
(2 + 3) + 4 = 5 + 4 = 9
2 + (3 + 4) = 2 + 7 = 9
Both ways of grouping give us the same answer! This property helps make math easier and more flexible.
Key Concept
Changing the grouping of numbers in addition doesn't change the sum. Only the parentheses move!
Why is the Associative Property Important?

The associative property is important because it:
1. Makes mental math easier: We can group numbers that are easier to add first.
2. Helps solve complex problems: It allows us to rearrange calculations to make them simpler.
3. Builds algebra skills: Understanding grouping helps when learning more advanced math.
Let's see how it helps with mental math:
Suppose you need to add: 17 + 25 + 5
Using the associative property:
Instead of adding 17 + 25 first (which gives 42), then 42 + 5 = 47...
We can group 25 + 5 first: (25 + 5) = 30
Then 17 + 30 = 47
Adding 25 + 5 to make 30 is much easier than adding 17 + 25!
Remember
The associative property only works for addition and multiplication - not for subtraction or division!
Associative vs. Commutative Property
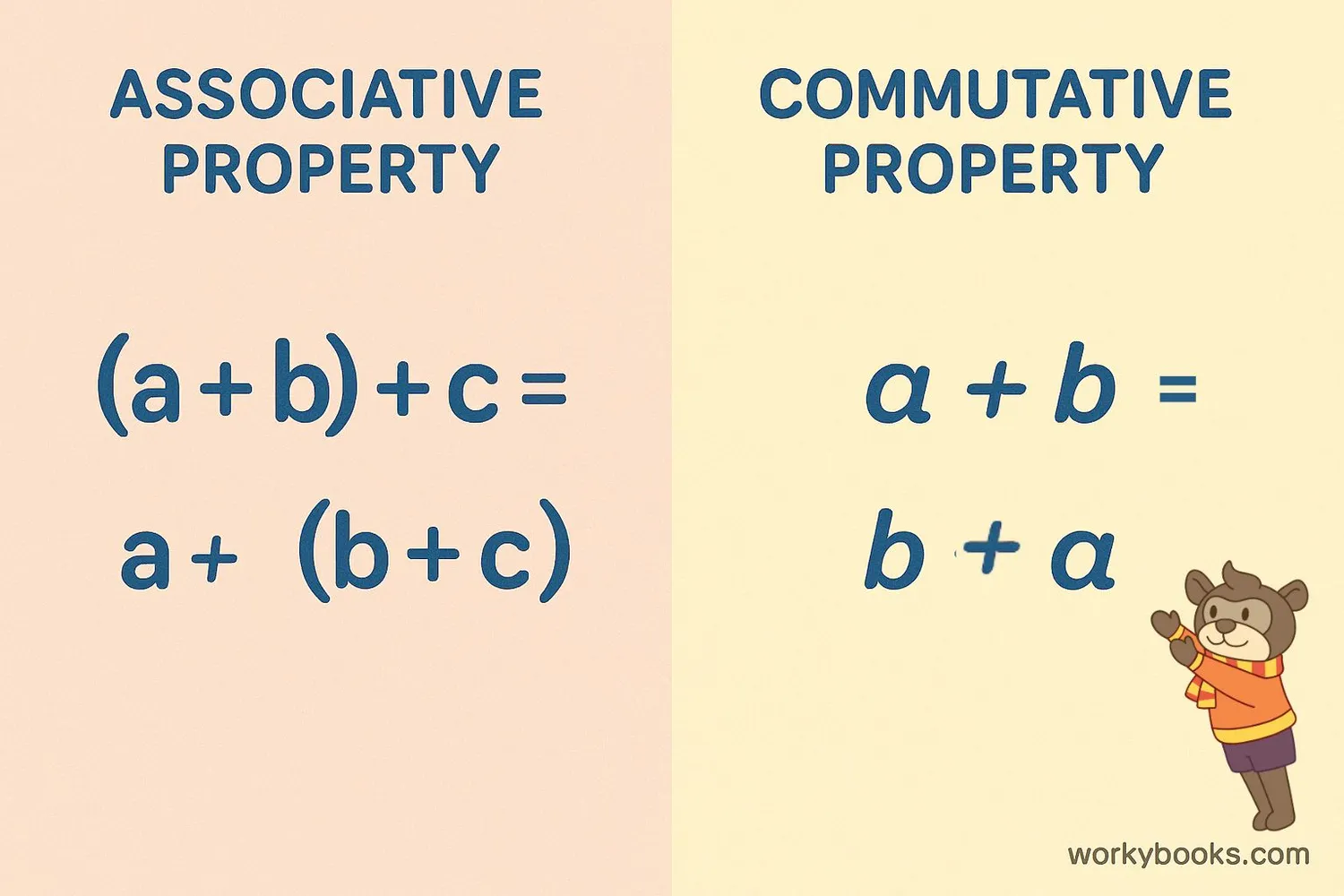
It's easy to confuse the associative property with the commutative property. Let's understand the difference:
Associative Property
Changes the grouping of numbers
Example:
(2 + 3) + 4 = 2 + (3 + 4)
Commutative Property
Changes the order of numbers
Example:
5 + 8 = 8 + 5
These two properties often work together to help us rearrange and simplify addition problems.
Math Tip
Remember: Associative = Grouping, Commutative = Order. Both make addition flexible!
Examples of Associative Property
Let's look at more examples to understand how the associative property works:
Example 1: With whole numbers
(15 + 7) + 3 = 22 + 3 = 25
15 + (7 + 3) = 15 + 10 = 25
Example 2: With decimals
(2.5 + 1.5) + 4.0 = 4.0 + 4.0 = 8.0
2.5 + (1.5 + 4.0) = 2.5 + 5.5 = 8.0
Example 3: With fractions
(1/2 + 1/4) + 1/4 = 3/4 + 1/4 = 1
1/2 + (1/4 + 1/4) = 1/2 + 2/4 = 1/2 + 1/2 = 1
Real-World Example: Adding apples
You have 4 red apples, 3 green apples, and 2 yellow apples.
Grouping 1: (4 red + 3 green) + 2 yellow = 7 + 2 = 9 apples
Grouping 2: 4 red + (3 green + 2 yellow) = 4 + 5 = 9 apples
The total is the same no matter how you group them!
Practice Time
Try solving: (18 + 6) + 4 and 18 + (6 + 4). Do you get the same answer?
Associative Property Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the associative property:
Math Trivia
Discover interesting facts about math properties:
Ancient Origins
The concept of mathematical properties like associativity dates back to ancient Greek mathematicians. Euclid's "Elements" (300 BC) contains early ideas about mathematical properties.
Beyond Numbers
The associative property applies to many mathematical concepts beyond numbers, including matrices, vectors, and complex algebraic structures in advanced mathematics.
Computer Science
In computer programming, the associative property affects how calculations are processed. Compilers use this property to optimize mathematical operations for faster execution.
Mental Math Champions
World champion mental calculators use properties like associativity to break complex problems into simpler parts. Some can add 10-digit numbers in seconds using these techniques!





