Associative Property of Multiplication - Definition, Examples, Quiz, FAQ, Trivia
Learn how grouping numbers differently doesn't change the product
What is the Associative Property?
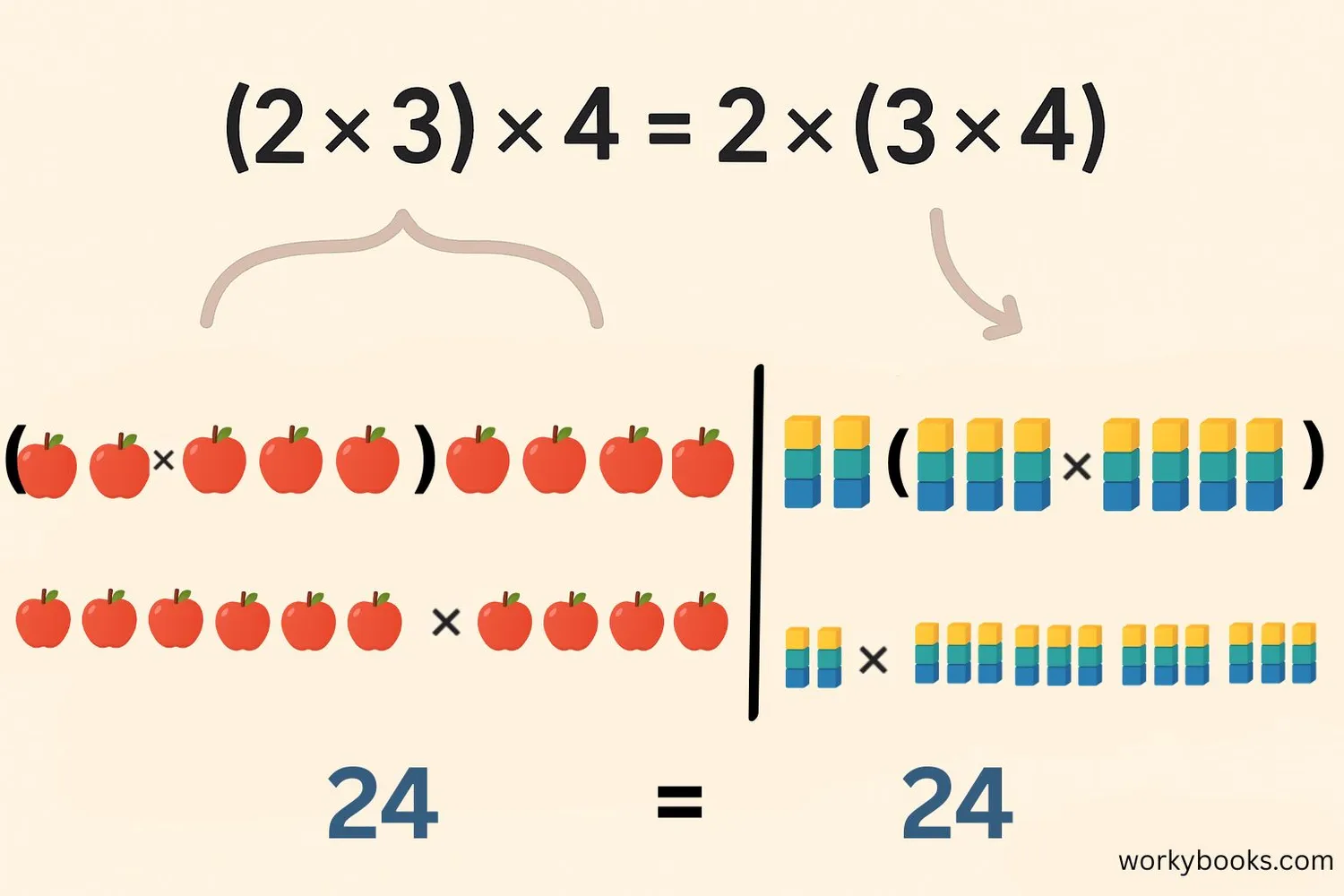
The associative property of multiplication is a special rule in mathematics. It tells us that when we multiply three or more numbers together, the way we group them doesn't change the final answer (the product).
Think of it like this: if you have a set of building blocks, it doesn't matter how you group them together when you count them - the total number will be the same. This property makes multiplication more flexible and helps us solve problems in different ways.
For example: (2 × 3) × 4 = 2 × (3 × 4). Both ways give us 24! This property only works for addition and multiplication - not for subtraction or division.
Key Concept
The associative property means: (a × b) × c = a × (b × c). The grouping of numbers doesn't affect the product.
Definition
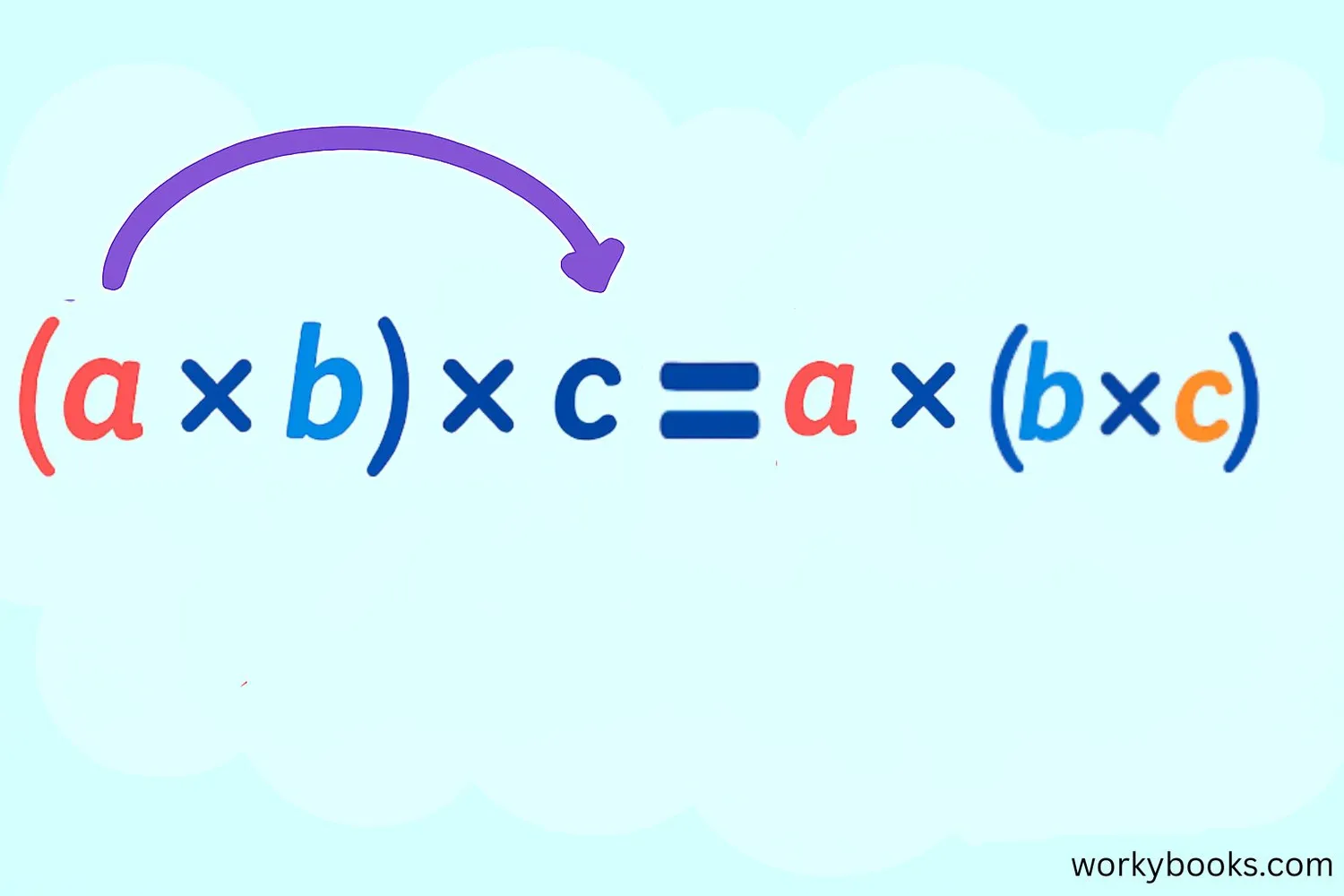
The associative property of multiplication states that when multiplying three or more numbers, the product is the same regardless of how the numbers are grouped.
Mathematical Definition
For any three numbers a, b, and c, changing the grouping doesn't change the result.
Important: The associative property is different from the commutative property. The commutative property says that changing the order of numbers doesn't change the product (a × b = b × a). The associative property is about grouping, not order.
Remember
The associative property only applies to addition and multiplication. It does not work for subtraction or division.
Examples
Let's explore some examples to understand how the associative property works:
Example 1: Numbers
Left side: (5 × 2) = 10, then 10 × 3 = 30
Right side: (2 × 3) = 6, then 5 × 6 = 30
Both groupings give the same result: 30
Example 2: Variables
No matter what numbers x, y, and z represent, both sides will be equal.
Example 3: Larger Numbers
Left side: (4 × 25) = 100, then 100 × 17 = 1,700
Right side: (25 × 17) = 425, then 4 × 425 = 1,700
Both groupings give the same result: 1,700
Example 4: With More Numbers
Left side: 4 × 5 = 20, then 3 × 20 = 60, then 2 × 60 = 120
Right side: 2 × 3 = 6 and 4 × 5 = 20, then 6 × 20 = 120
Both groupings give the same result: 120
Practice Tip
Look for groupings that make multiplication easier. For example: 5 × (8 × 4) = (5 × 8) × 4 = 40 × 4 = 160
Why Is the Associative Property Important?
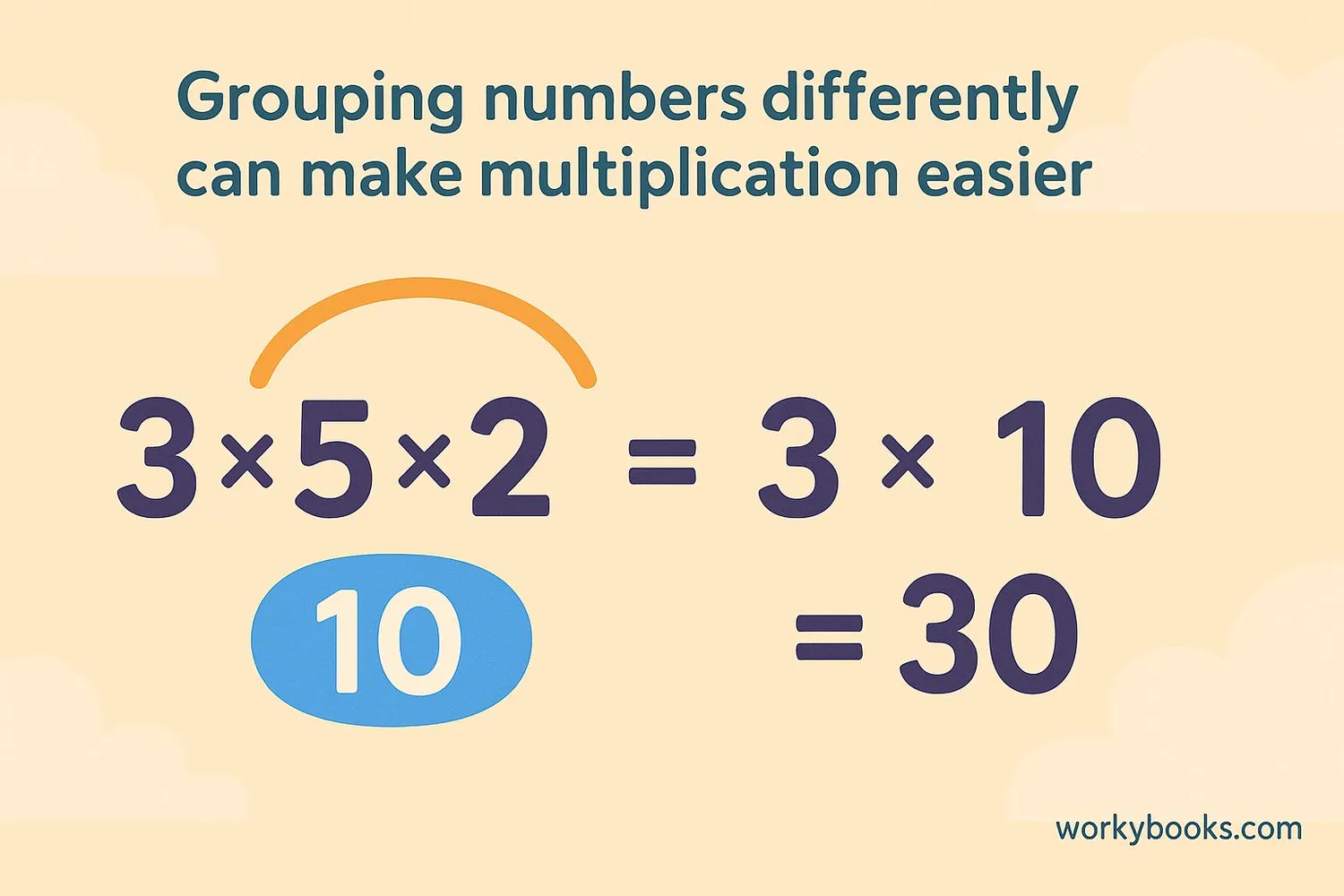
The associative property is important for several reasons:
1. Flexibility in Calculations: It allows us to group numbers in ways that make multiplication easier. For example, when multiplying several numbers, we can look for pairs that multiply to 10, 100, or other easy numbers.
2. Mental Math: This property helps us perform calculations in our head more easily. We can rearrange the grouping to simplify the process.
3. Algebraic Manipulations: In algebra, the associative property allows us to regroup variables and constants to simplify expressions and solve equations.
4. Foundation for Advanced Math: Understanding this property helps build a foundation for more advanced mathematical concepts like matrix multiplication and abstract algebra.
5. Problem Solving: It gives us different ways to approach multiplication problems, making us more versatile mathematicians.
Without the associative property, math would be much more rigid and difficult!
Real-World Application
When calculating total items in multiple boxes of multiple packages, the associative property allows us to group the numbers in the most efficient way.
Comparing Multiplication Properties

Multiplication has several important properties. Let's compare them:
| Property | Rule | Example | What It Means |
|---|---|---|---|
| Associative | (a × b) × c = a × (b × c) | (2 × 3) × 4 = 2 × (3 × 4) | Grouping doesn't change the product |
| Commutative | a × b = b × a | 5 × 4 = 4 × 5 | Order doesn't change the product |
| Distributive | a × (b + c) = (a × b) + (a × c) | 3 × (4 + 5) = (3 × 4) + (3 × 5) | Multiplication distributes over addition |
| Identity | a × 1 = a | 7 × 1 = 7 | Multiplying by 1 doesn't change the number |
| Zero | a × 0 = 0 | 9 × 0 = 0 | Multiplying by 0 always gives 0 |
Key Difference
Associative is about grouping, commutative is about order, and distributive connects multiplication and addition.
Practice Quiz
Test your understanding of the associative property with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the associative property:
Math Trivia
Discover interesting facts about multiplication and properties:
Ancient Multiplication
The ancient Egyptians used a method called "doubling" for multiplication that relied on the associative property without knowing it. They would double numbers and add the appropriate doubles to get products.
Computer Calculations
Computers use the associative property to optimize calculations. When solving complex multiplication problems, they group numbers to minimize processing time and memory usage.
Beyond Numbers
The associative property applies to more than just numbers. It works with matrices in advanced mathematics, and even in everyday situations like combining ingredients in cooking.
Mental Math Champions
Mental math champions use properties like associative and commutative to solve problems faster. They regroup numbers to create easier multiplication problems, like multiplying by 10 or 100 first.





