Base Area of a Cone - Definition, Examples, Quiz, FAQ, Trivia
Learn about the circular base of cones with simple explanations and practice activities
What is the Base Area of a Cone?
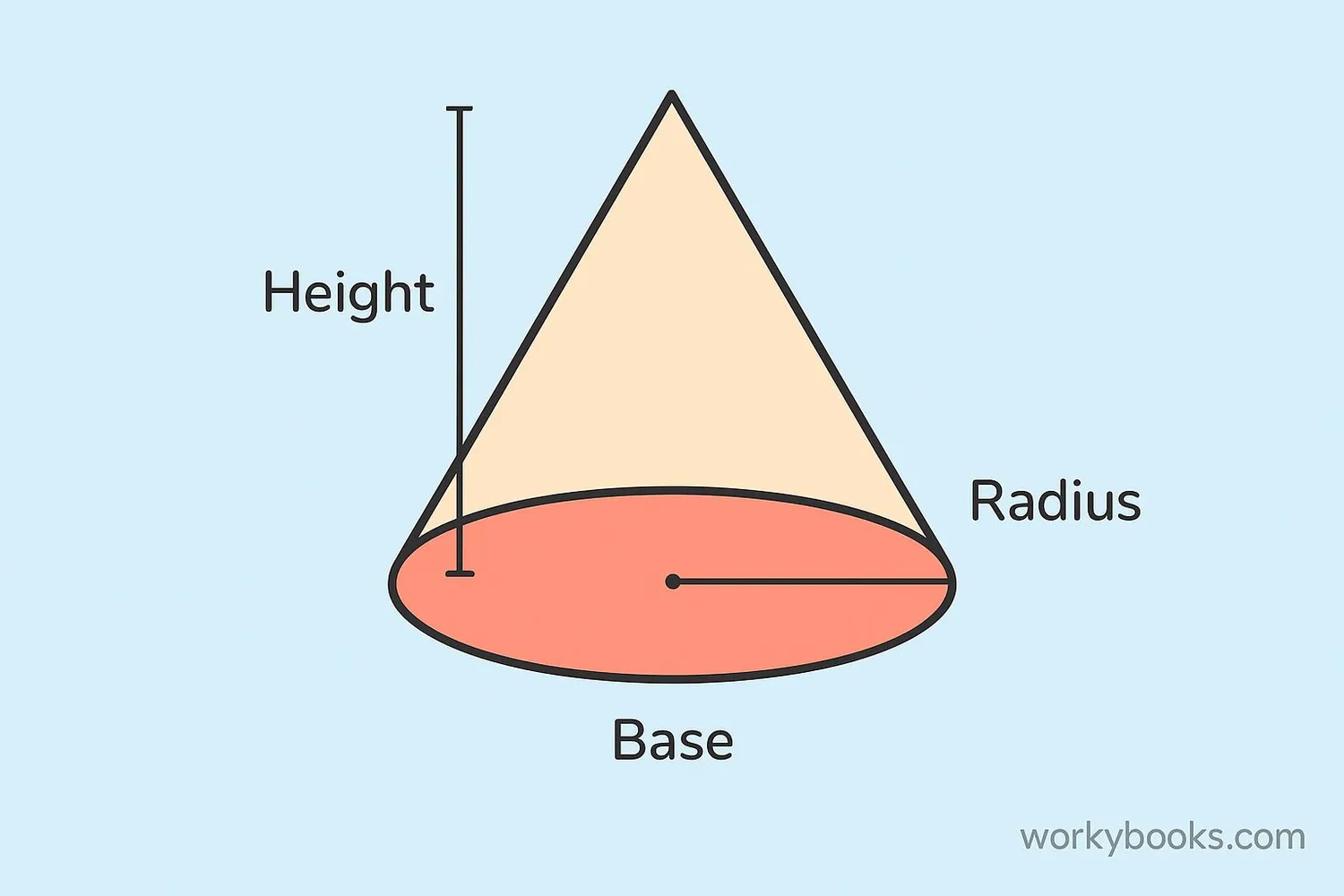
The base area of a cone is the area of its circular base. Since cones have a flat circular bottom, we calculate the base area using the same method we use for circles.
Why is this important? The base area helps us understand how much space the cone occupies on a surface. It's also a key part of calculating the cone's total surface area and volume.
Remember: All cones have a circular base. This circle is what makes the base area calculation possible using the circle area formula.
Key Concept
The base area of a cone is always a circle. To find its area, we use the same formula we use for circles.
Formula for Base Area
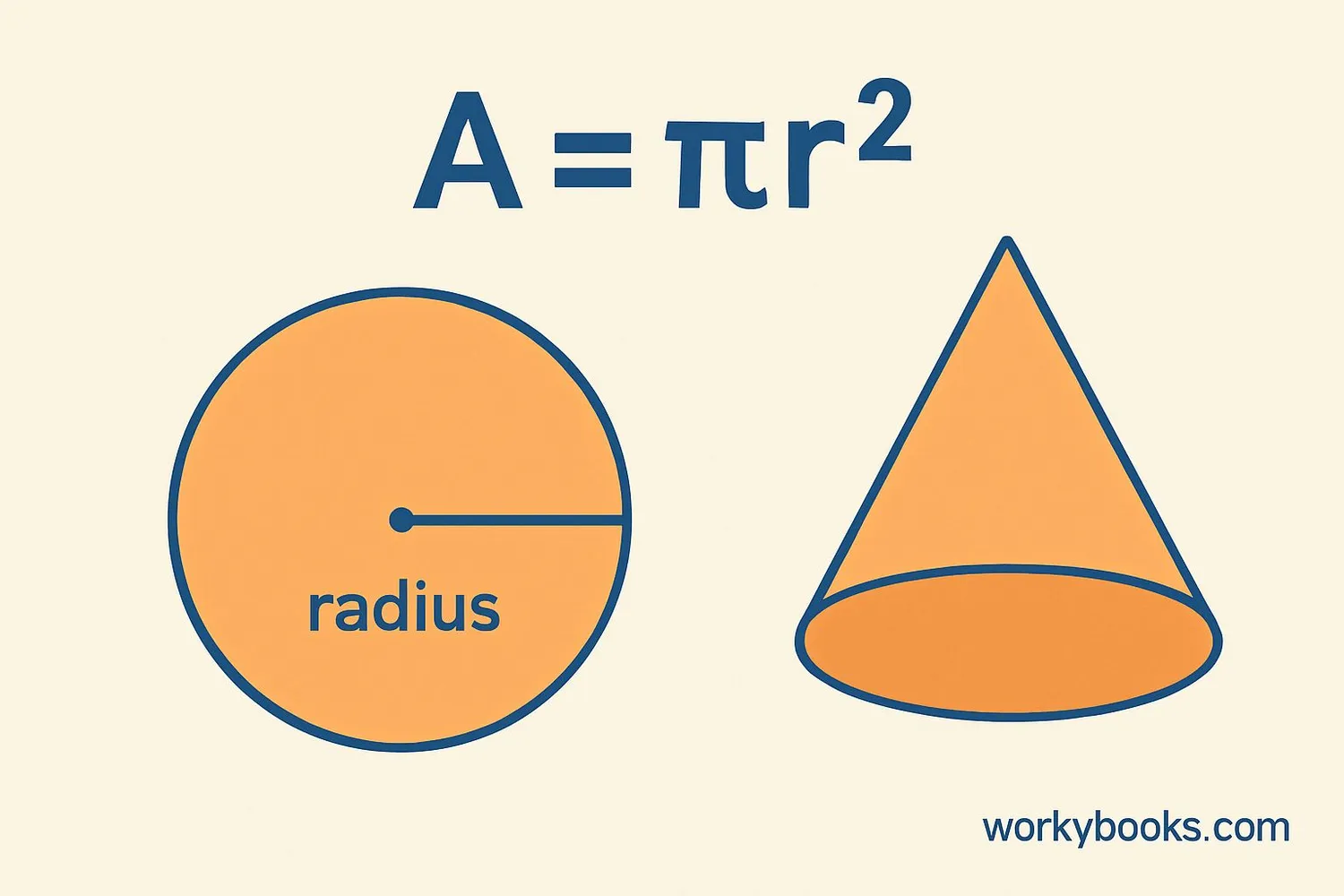
The formula for calculating the base area of a cone is simple:
Base Area Formula
Where:
A = Base area
π (pi) ≈ 3.14159
r = Radius of the base circle
Pi (π) is a special number in mathematics that represents the ratio of a circle's circumference to its diameter. We often use the approximation 3.14 for calculations.
Remember
The base area depends only on the radius of the base circle, not on the height of the cone.
How to Calculate Base Area
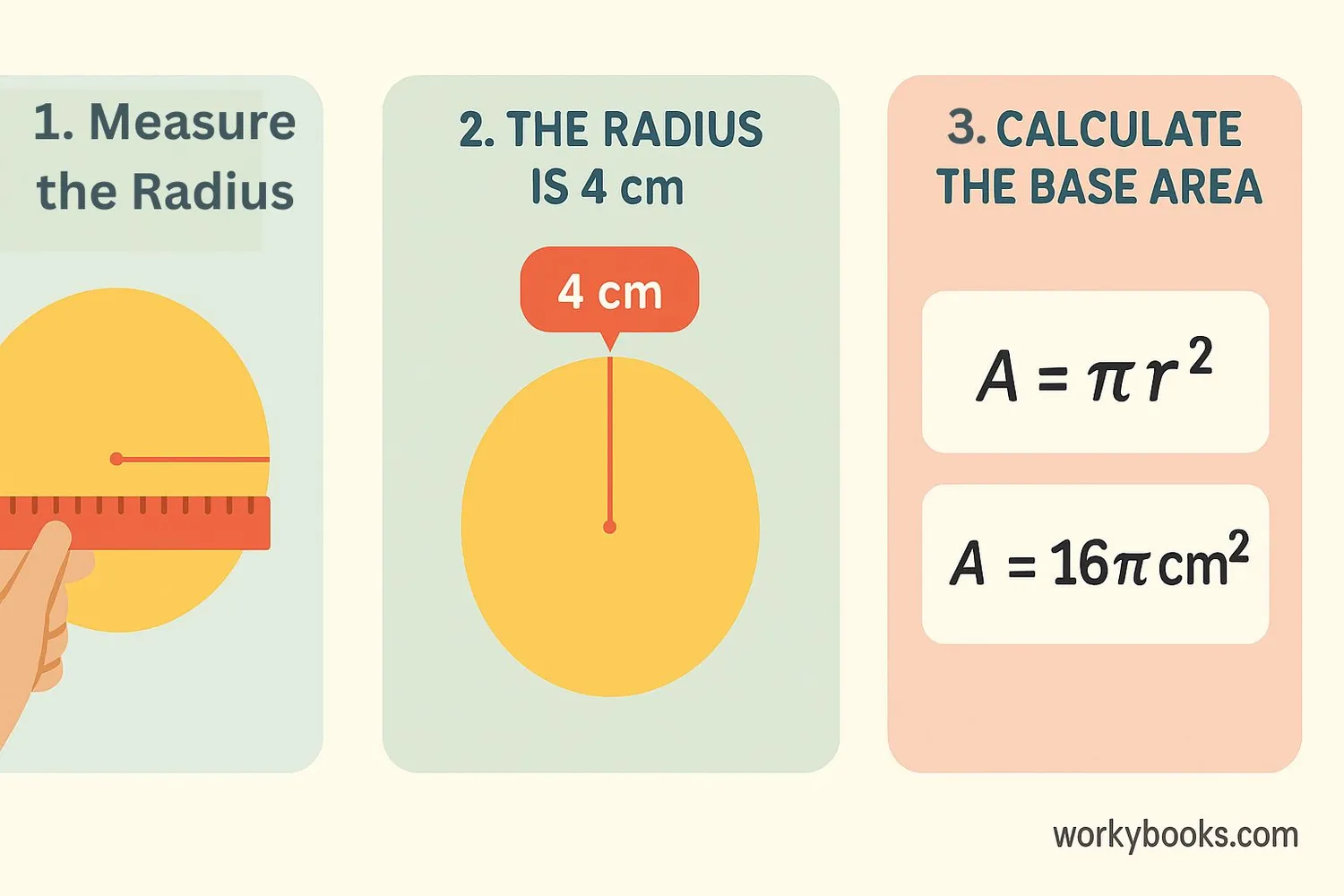
Let's learn how to calculate the base area step by step:
Step 1: Measure the radius of the base circle. The radius is the distance from the center of the circle to its edge.
Step 2: Square the radius (multiply it by itself).
Step 3: Multiply the squared radius by pi (π ≈ 3.14).
Example: If a cone has a base radius of 5 cm:
Step 1: Radius (r) = 5 cm
Step 2: r² = 5 × 5 = 25
Step 3: A = π × 25 ≈ 3.14 × 25 = 78.5 cm²
So the base area is approximately 78.5 square centimeters.
Calculation Tip
Always include units in your answer. Since area measures surface, it should be in square units (cm², m², etc.).
Examples
Let's practice with some real-world examples:
Example 1: An ice cream cone has a base radius of 2 cm. What is its base area?
Solution: A = πr² = 3.14 × (2 × 2) = 3.14 × 4 = 12.56 cm²
Example 2: A traffic cone has a base radius of 15 cm. Calculate its base area.
Solution: A = πr² = 3.14 × (15 × 15) = 3.14 × 225 = 706.5 cm²
Example 3: A party hat has a base circumference of 31.4 cm. What is its base area?
Solution: First find the radius from circumference: C = 2πr → 31.4 = 2 × 3.14 × r → r = 31.4 ÷ 6.28 = 5 cm
Then A = πr² = 3.14 × (5 × 5) = 3.14 × 25 = 78.5 cm²
Example 4: A conical tent has a base area of 38.465 m². What is its radius?
Solution: A = πr² → 38.465 = 3.14 × r² → r² = 38.465 ÷ 3.14 = 12.25 → r = √12.25 = 3.5 m
Practice Tip
Try measuring circular objects around you and calculate their area. This will help you understand the base area concept better!
Practice Quiz
Test your understanding of cone base area with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about the base area of a cone:
Geometry Trivia
Discover interesting facts about cones and geometry:
Ancient Geometry
The study of cones dates back to ancient Greek mathematicians. Euclid wrote about cones in his famous work "Elements" around 300 BC.
Cones in Nature
Pine cones are excellent examples of natural cones. Their spiral patterns follow the Fibonacci sequence, a famous mathematical pattern.
Architectural Cones
The world's largest cone-shaped structure is the San Jacinto Monument in Texas, standing 173.7 meters (570 feet) tall with a base diameter of 47 meters (154 feet).
Cone Volume
A cone holds exactly one-third the volume of a cylinder with the same base and height. This relationship was discovered by Archimedes over 2,000 years ago!


