Base Area of a Triangular Prism - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate the base area of triangular prisms with easy explanations and practice activities
What is the Base Area of a Triangular Prism?
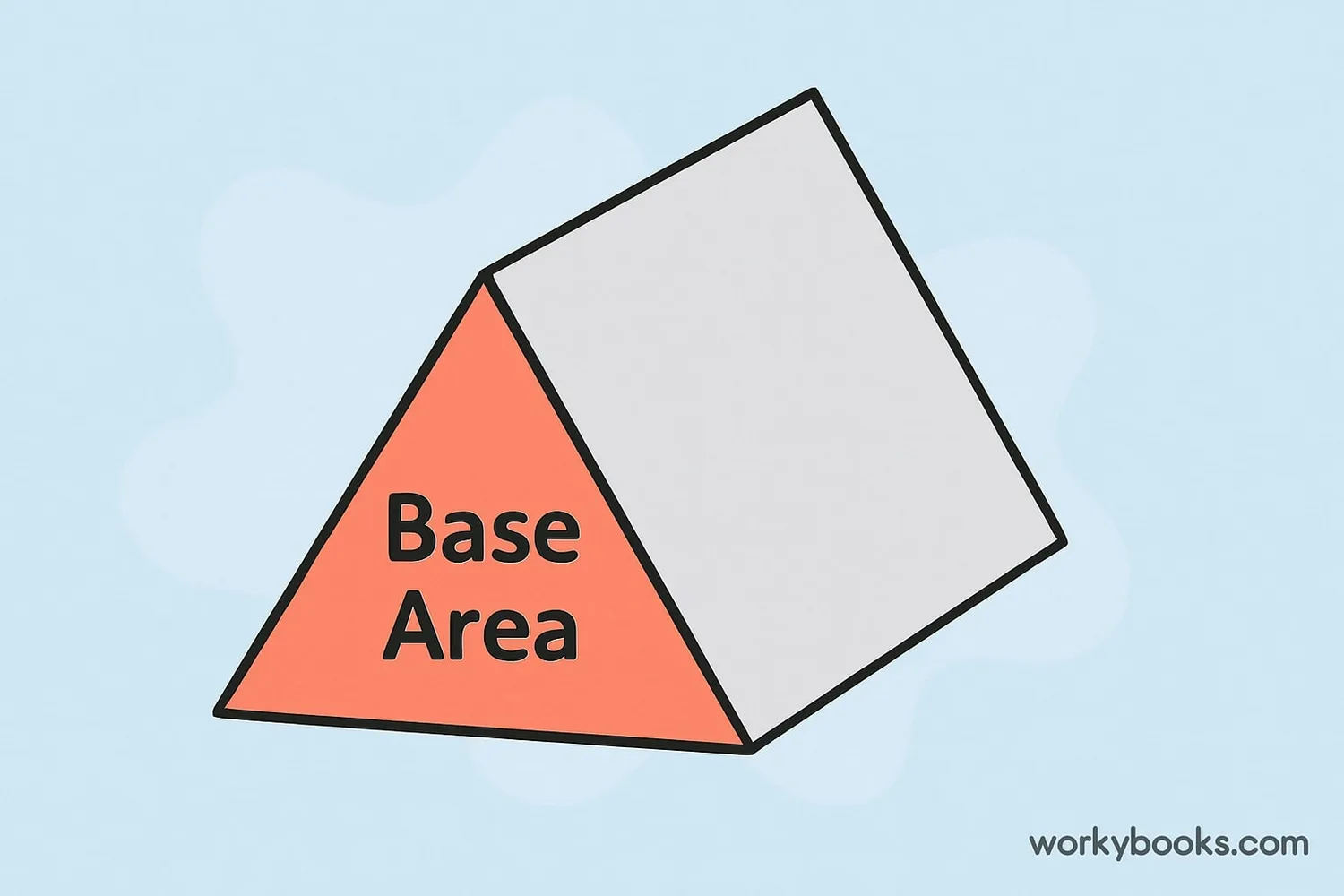
The base area of a triangular prism is the area of one of its triangular bases. A triangular prism has two identical triangular bases and three rectangular sides.
Think of it like a tent: the triangular ends are the bases, and the fabric connecting them forms the rectangular sides. The base area is simply the area of one of those triangular ends.
To find the base area, we use the formula for the area of a triangle: Area = ½ × base × height. This is the same formula you use for any triangle!
Key Concept
The base area is the area of the triangular base, not the rectangular sides. Remember that a triangular prism has two identical triangular bases.
How to Find the Base Area
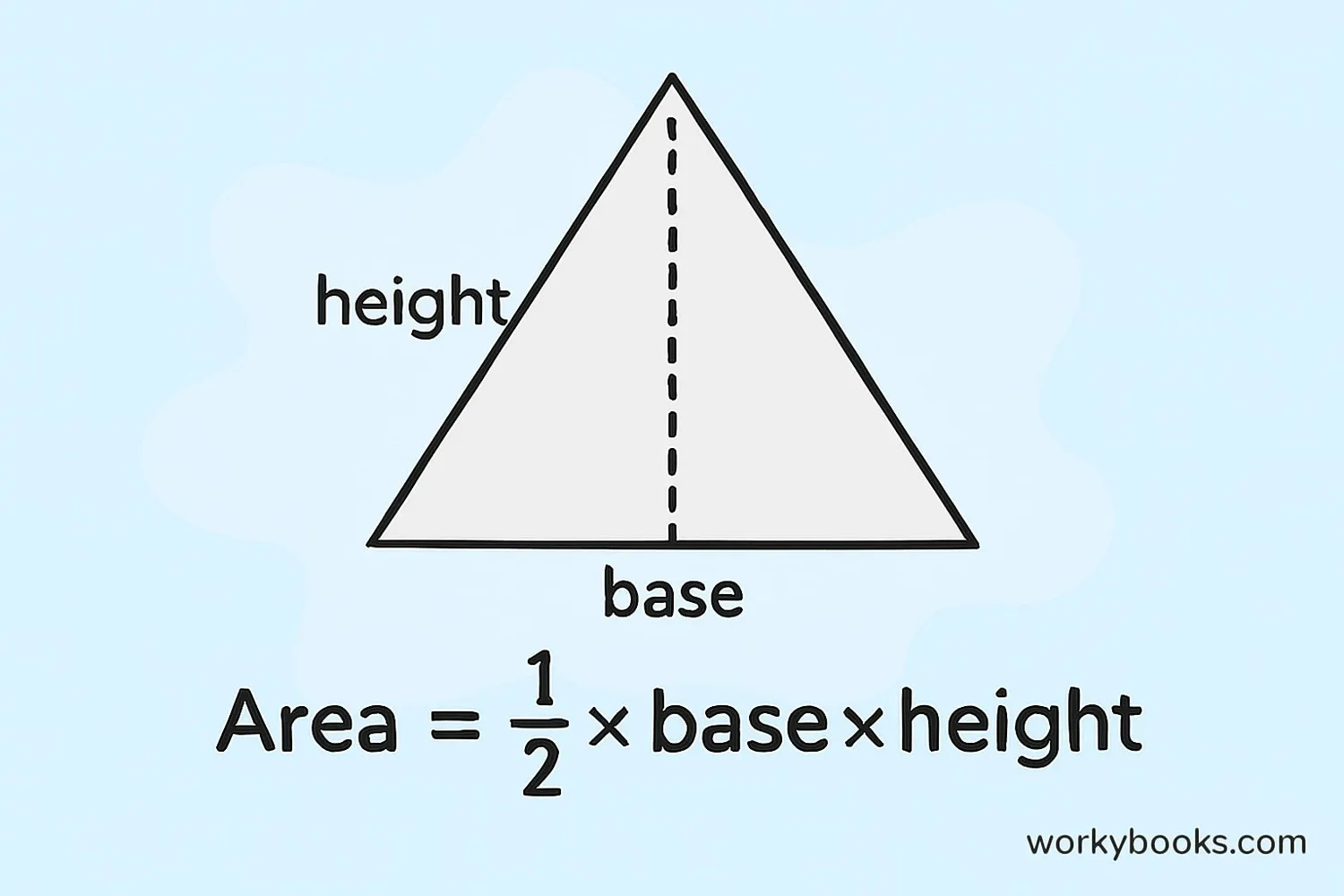
Finding the base area of a triangular prism is simple if you remember the formula for the area of a triangle:
Base Area Formula
Where:
A = Area of the triangular base
b = base length of the triangle
h = height of the triangle
1. Identify the base: This is one side of the triangle. It can be any side, but usually it's the bottom side.
2. Identify the height: This is the perpendicular distance from the base to the opposite vertex (corner). The height must be perpendicular to the base.
3. Apply the formula: Multiply the base length by the height, then divide by two (or multiply by 0.5).
Example 1
A triangular base has a base of 8 cm and height of 5 cm. What is its area?
Solution: A = ½ × 8 cm × 5 cm = ½ × 40 cm² = 20 cm²
Remember
The height must be perpendicular to the base you're measuring. If you only know the sides of the triangle, you might need to use a different formula or find the perpendicular height.
Examples
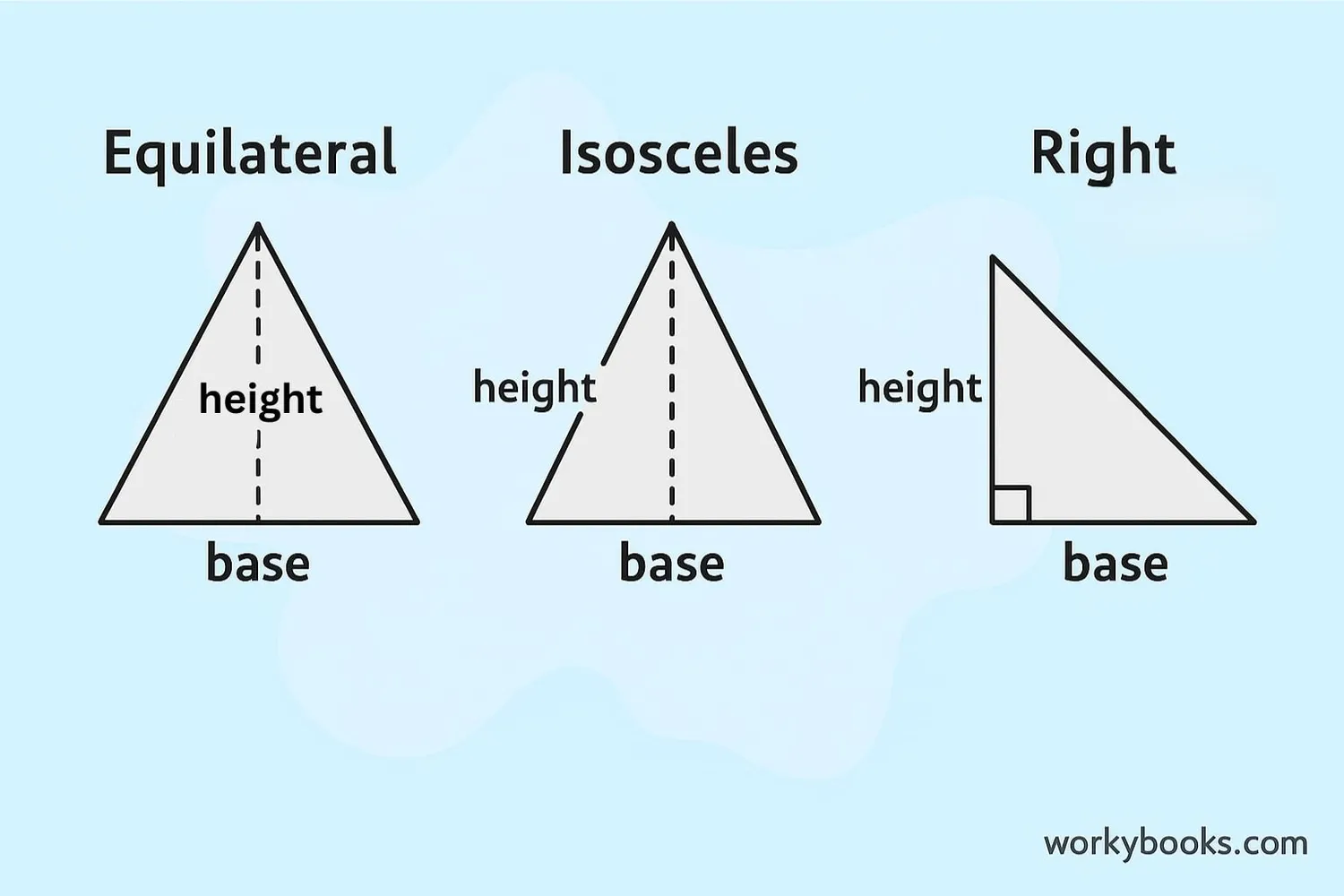
Let's practice finding base areas with different examples:
Example 1: Right Triangle
A triangular prism has a right triangular base with legs of 6 cm and 8 cm. What is the base area?
Solution: For a right triangle, the legs are the base and height. A = ½ × 6 cm × 8 cm = 24 cm²
Example 2: Equilateral TriangleAn equilateral triangular base has sides of 10 cm. The height is 8.66 cm. What is the base area?
Solution: A = ½ × 10 cm × 8.66 cm = 43.3 cm²
Example 3: Isosceles TriangleAn isosceles triangular base has a base of 12 cm and height of 8 cm. What is the base area?
Solution: A = ½ × 12 cm × 8 cm = 48 cm²
Practice Tip
Remember that the base area is only part of what makes up the entire prism. To find the volume, you'll multiply the base area by the length of the prism!
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about triangular prisms and base area:
Geometry Trivia
Discover interesting facts about geometry and triangular prisms:
Ancient Geometry
The concept of prisms dates back to ancient Egypt. The Great Pyramid of Giza is essentially a square pyramid, but the Egyptians understood and used triangular shapes in their architecture.
Strong Shapes
Triangles are the strongest geometric shape because any force applied to them is evenly distributed. That's why you see triangular supports in bridges, towers, and other structures that need strength.
Nature's Prisms
Some crystals form naturally as triangular prisms. Calcite crystals often grow as triangular prisms, and they can split light into different colors just like glass prisms.
Prisms and Light
Triangular prisms are famous for bending light. When white light passes through a triangular prism, it separates into all the colors of the rainbow - this is called dispersion.





