Base-Ten Numerals - Definition, Examples, Quiz, FAQ, Trivia
Understanding our number system with place value and base ten blocks
What are Base-Ten Numerals?
Base-ten numerals are the numbers we use every day - 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. They're called "base-ten" because our number system is based on groups of ten.
This means that when we count, we use ten different digits (0-9). When we get to 10, we don't have a new digit, so we write 10 to mean "one group of ten and zero ones". This is why it's called the decimal system - from the Latin word "decem" meaning ten.
Base-ten numerals are used all around the world and make it easy to write and understand numbers of any size. Without base-ten numerals, math would be much harder!
Key Concept
Our number system has only ten digits (0-9), but we can represent any number by using place value - the position of each digit tells us its value.
Base Ten Blocks
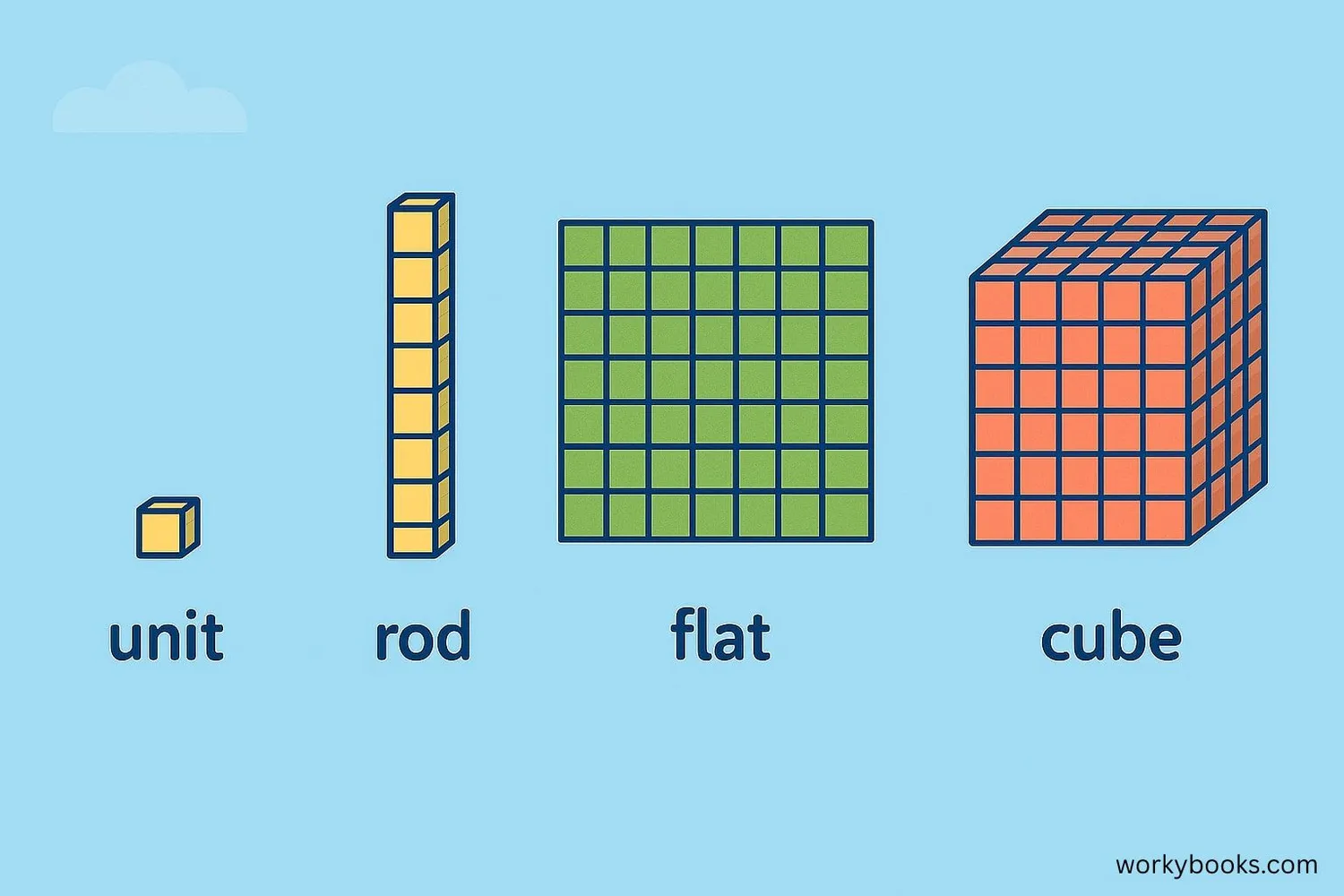
Base ten blocks are special tools that help us understand numbers visually. They come in four main types:
Units (ones): Small cubes that represent 1
Rods (tens): Long blocks made of 10 units
Flats (hundreds): Square blocks made of 10 rods (100 units)
Cubes (thousands): Large cubes made of 10 flats (1,000 units)
Using base ten blocks makes it easier to understand how numbers are made up. For example, the number 243 would be:
2 flats (200) + 4 rods (40) + 3 units (3) = 243
Remember
Each time you move to a larger block, you're multiplying by 10. This is the foundation of our base-ten system!
Place Value
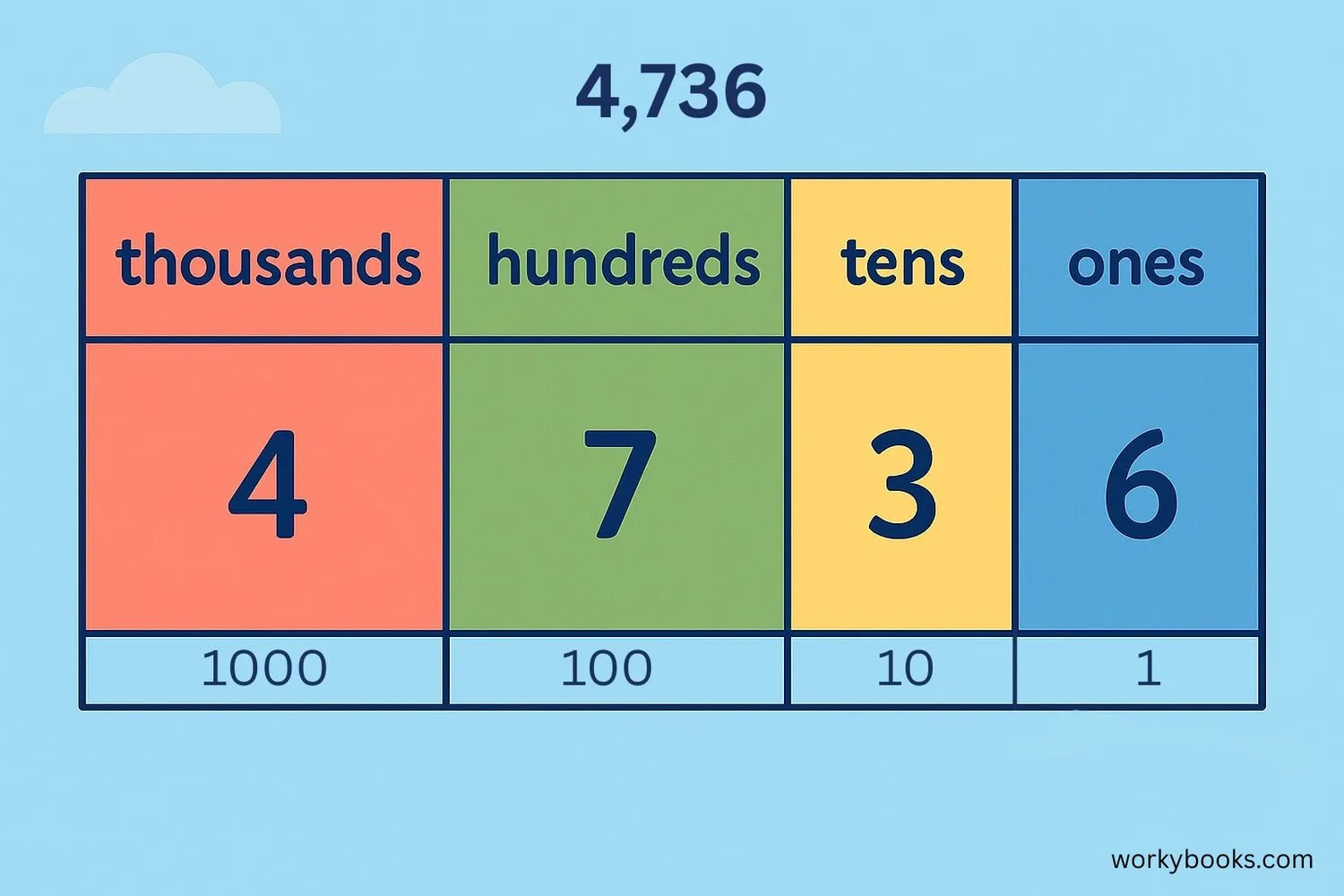
Place value means that the position of a digit in a number determines its value. In our base-ten system, each place is ten times larger than the place to its right.
| Thousands | Hundreds | Tens | Ones |
|---|---|---|---|
| 1,000 | 100 | 10 | 1 |
| 2 | 4 | 7 | 5 |
In the number 2,475:
The 2 is in the thousands place: 2 × 1,000 = 2,000
The 4 is in the hundreds place: 4 × 100 = 400
The 7 is in the tens place: 7 × 10 = 70
The 5 is in the ones place: 5 × 1 = 5
So 2,000 + 400 + 70 + 5 = 2,475
Place Value Tip
Each time you move left one place, you multiply by 10. Each time you move right, you divide by 10.
Expanded Form

Expanded form is a way to write numbers by showing the value of each digit. It helps us understand how numbers are built from their place value components.
For example, the number 347 in expanded form is:
We can see that 347 is made up of 3 hundreds, 4 tens, and 7 ones.
Let's try a larger number: 5,208
Notice that we include the tens place even though it has a 0: 5,000 + 200 + 0 + 8
Expanded form makes it easier to:
- Understand how numbers are composed
- Compare numbers
- Add and subtract large numbers
Expanded Form Tip
Always write the expanded form with the largest place value first, then work down to the ones place.
Base-Ten Practice Quiz
Test your understanding of base-ten numerals with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about base-ten numerals:
Number System Trivia
Discover interesting facts about numbers and counting systems:
Ancient Number Systems
The earliest known number system dates back 20,000 years to bones with tally marks. The ancient Egyptians used a base-10 system around 3000 BCE, but they didn't have a symbol for zero.
Animals That Count
Some animals show basic number sense! Bees can count landmarks, chimpanzees can learn to count objects, and some fish can tell the difference between small quantities. But humans are the only species with a complex number system.
Largest Named Number
The largest number with a name is "googolplex" - that's 1 followed by a googol of zeros! A googol is 10¹⁰⁰ (1 followed by 100 zeros). There aren't that many particles in the entire observable universe!
Zero's Journey
The concept of zero was developed independently by ancient Babylonians, Mayans, and Indians. The Indian mathematician Brahmagupta established rules for zero around 628 CE. It took centuries for zero to spread to Europe where it was initially distrusted.





