Benchmark Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn how to use benchmarks for estimation and comparison in mathematics
What is a Benchmark Number?
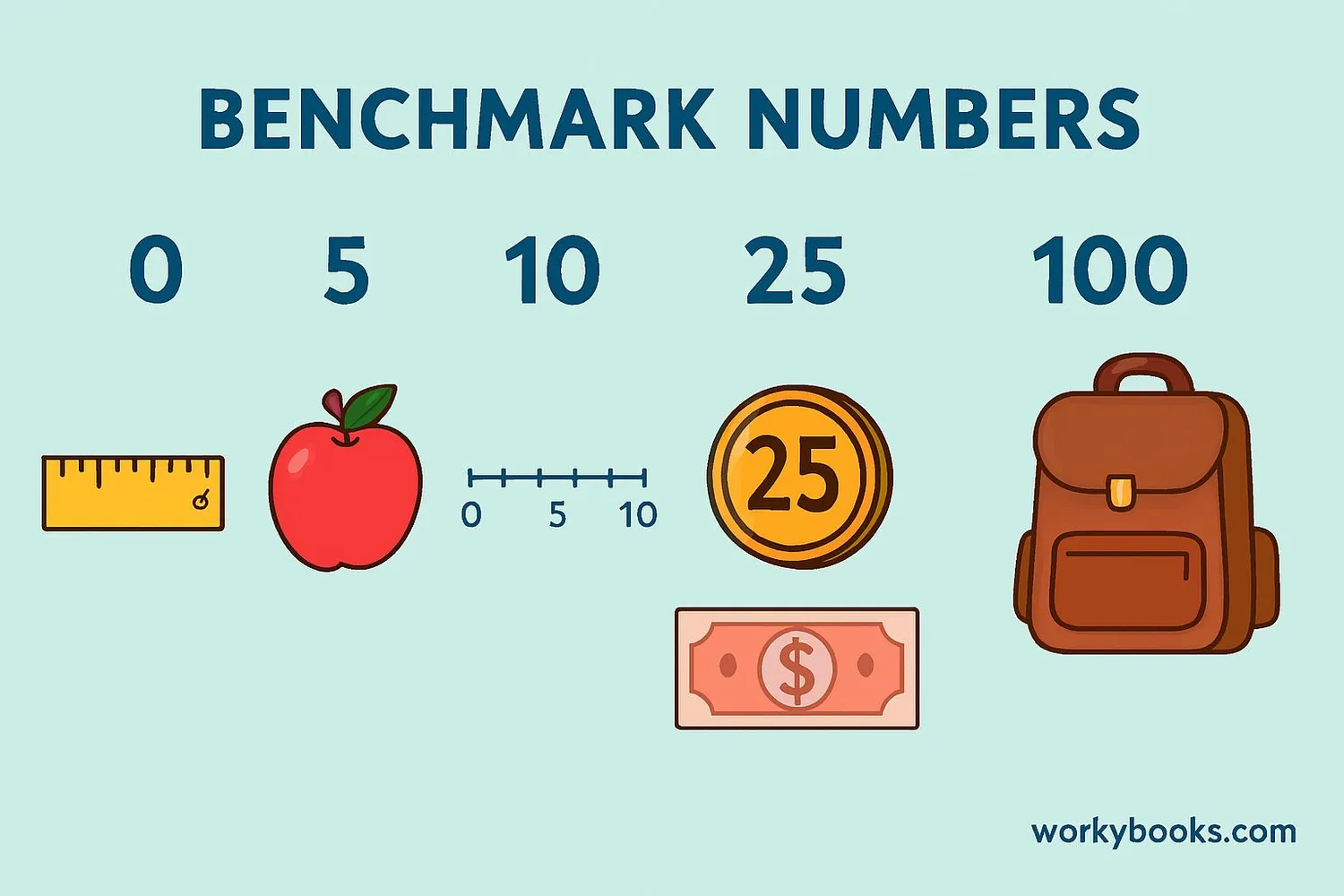
A benchmark number is a familiar number that we can use as a reference point to help us estimate, compare, or understand other numbers. Think of benchmarks as friendly numbers that make math easier!
In mathematics, benchmark numbers are special because:
- They are easy to recognize and remember
- We can use them to quickly estimate quantities
- They help us compare different numbers
- They make complex problems simpler to understand
Common benchmark numbers include 0, 5, 10, 25, 50, 100, and 1000. These numbers act like helpful landmarks on the number line that we can use to navigate mathematical problems.
Key Concept
Benchmark numbers are reference points that make estimation and comparison easier in mathematics.
How to Use Benchmark Numbers
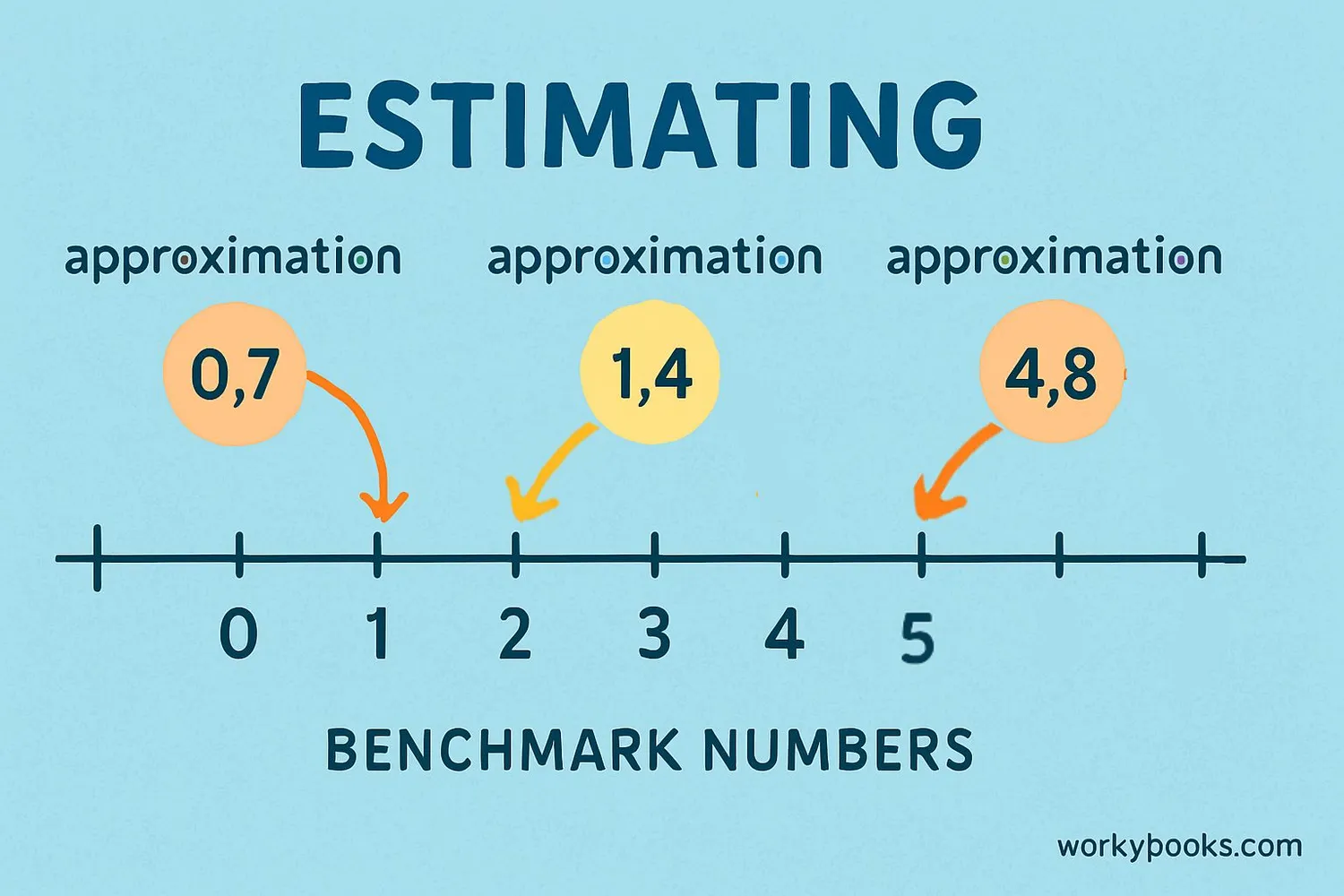
Using benchmark numbers helps us solve math problems more easily. Here's how to use them:
Step 1: Identify an appropriate benchmark number near the number you're working with
Step 2: Compare your number to the benchmark
Step 3: Use the benchmark to estimate or calculate
Let's look at an example with fractions:
Example: Comparing Fractions
Is 3/8 greater than or less than 1/2?
We know that 1/2 is a benchmark fraction. Since 3/8 is less than 4/8 (which equals 1/2), we can say that 3/8 < 1/2.
- Rounding numbers
- Estimating sums and differences
- Comparing fractions
- Understanding place value
Common Benchmark Numbers
Real-World Examples
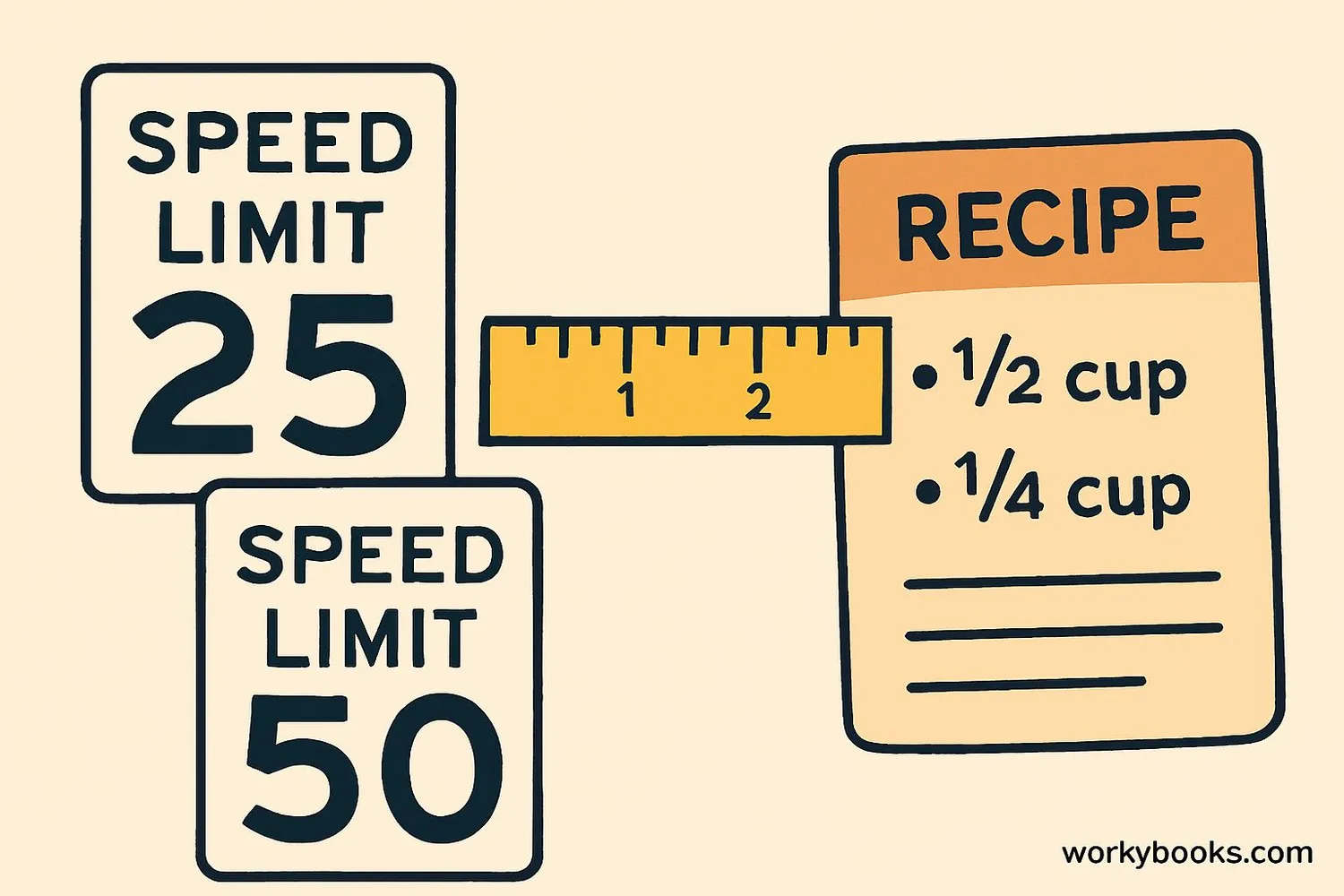
We use benchmark numbers every day without even realizing it! Here are some real-world examples:
Example 1: Money
When you have $0.78, you know it's close to $0.75 (which is 3 quarters) or $0.80. The benchmark $1.00 helps you understand how much money you have.
Example 2: Time
If it's 11:45, you know it's 15 minutes before noon. The benchmark times (quarter past, half past, quarter to) help you estimate time.
Example 3: Measurement
If a bookshelf is 47 inches tall, you know it's close to 48 inches (4 feet). The benchmark of 4 feet helps you understand the height.
Example 4: Temperature
When it's 33°F, you know it's just above freezing (32°F). The benchmark of 32°F helps you dress appropriately.
Practice Activity
Find five benchmark numbers in your home or classroom. Where do you see 10, 25, 50, 100 or 1000? (Examples: page numbers, measurement markings, packaging quantities)
Benchmark Quiz
Test your understanding of benchmark numbers with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about benchmark numbers:
Math Measurement Trivia
Discover interesting facts about numbers and measurement:
Origin of Numbers
The number system we use today originated in India around 500 CE. It was later adopted by Arabic mathematicians, which is why we call them "Arabic numerals."
The Power of 10
Our number system is based on 10 because humans have 10 fingers. This is called a "base-10" or "decimal" system. Some ancient cultures used base-12 or base-60 systems!
Standard Measurements
The metric system was created during the French Revolution to establish standard measurements. Today, almost all countries use the metric system except the United States, Liberia, and Myanmar.
Googol and Googolplex
A googol is 1 followed by 100 zeros. A googolplex is 1 followed by a googol of zeros! These huge numbers were named by a 9-year-old boy, Milton Sirotta, in 1938.





