Benchmark Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn to compare and estimate fractions using common reference points
What are Benchmark Fractions?
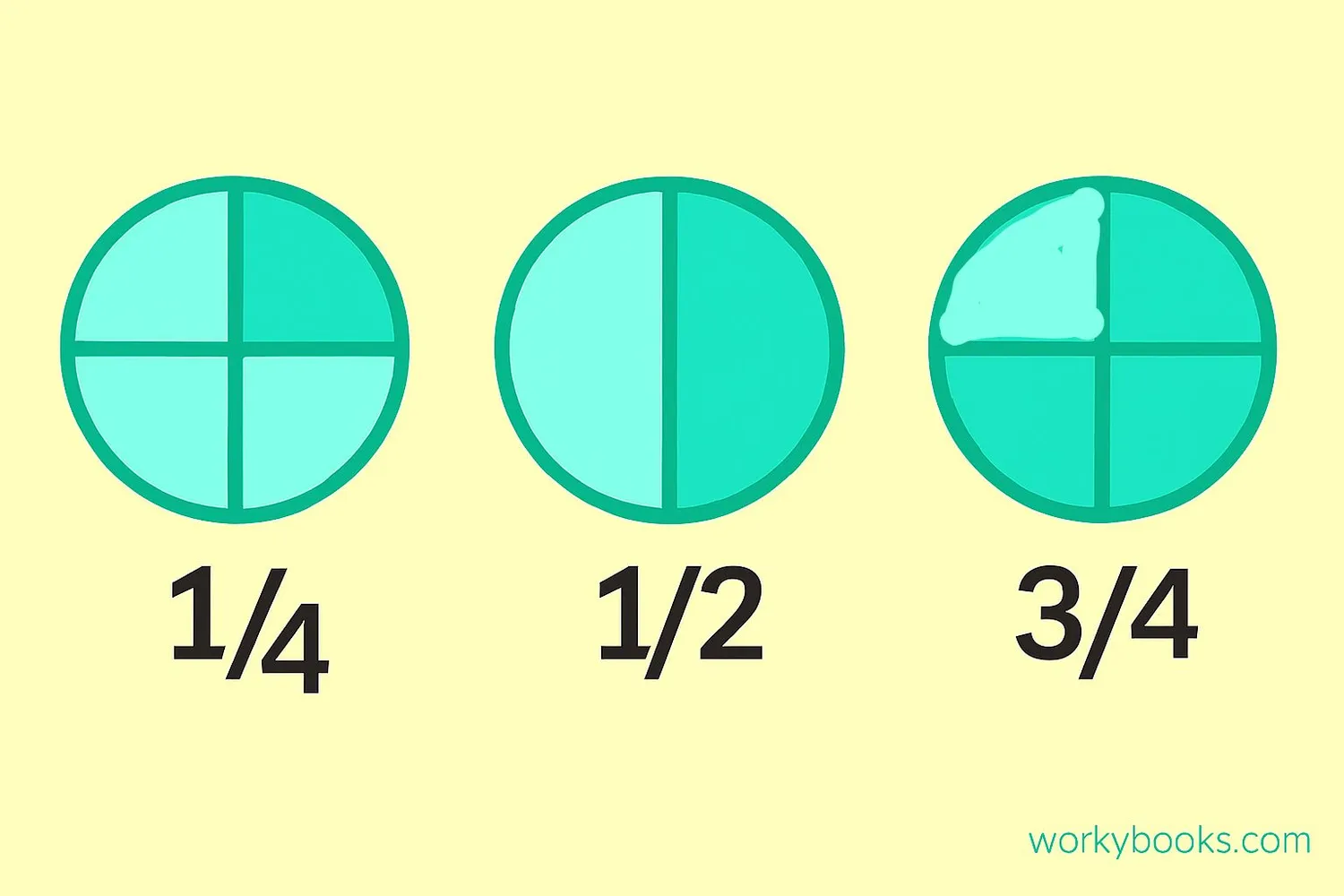
Benchmark fractions are common fractions that we use as reference points to help us understand, estimate, and compare other fractions. They're like familiar landmarks on a map that help us find our way in the world of fractions.
The most important benchmark fractions are:
- 0 (zero)
- 1/2 (one-half)
- 1 (one whole)
We also often use:
- 1/4 (one-quarter)
- 3/4 (three-quarters)
- 1/3 (one-third)
- 2/3 (two-thirds)
These fractions are special because they're easy to visualize and understand. When we see a new fraction, we can compare it to these benchmarks to quickly get an idea of its size.
Key Concept
Benchmark fractions help us estimate and compare other fractions without doing complicated calculations.
Common Benchmark Fractions
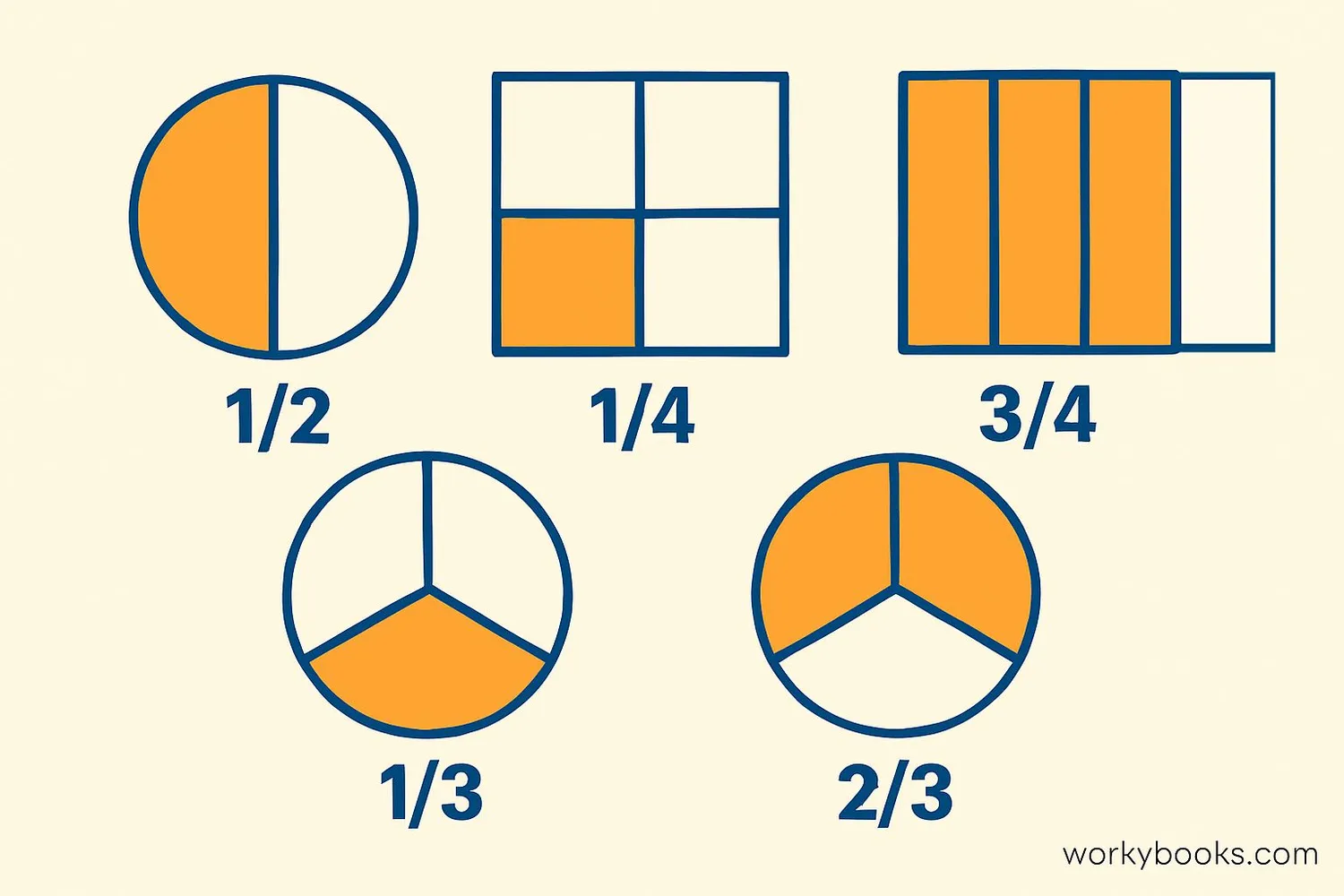
Let's look at some common benchmark fractions and what they represent:
0: This represents nothing or zero. Any fraction smaller than our benchmarks starts here.
1/2: This is exactly halfway between 0 and 1. It's our most important benchmark! Fractions less than 1/2 are closer to 0, while fractions greater than 1/2 are closer to 1.
1: This represents one whole. Fractions larger than 1 are greater than a whole.
1/4 and 3/4: These are halfway between 0 and 1/2, and halfway between 1/2 and 1. They help us make more precise estimates.
1/3 and 2/3: These are useful when dividing things into three equal parts. 1/3 is a little less than 1/2, and 2/3 is a little more than 1/2.
Remember
When you see a fraction, ask yourself: Is it closer to 0, to 1/2, or to 1? This simple question helps you understand the fraction's size!
Benchmark Fractions on a Number Line

A number line is a great way to visualize where benchmark fractions are located. Let's look at how they are arranged:
0 is at the far left, and 1 is at the far right. Right in the middle is 1/2.
Between 0 and 1/2, we have:
- 1/4 - halfway between 0 and 1/2
- 1/3 - a little more than 1/4 but less than 1/2
Between 1/2 and 1, we have:
- 2/3 - a little more than 1/2 but less than 3/4
- 3/4 - halfway between 1/2 and 1
Knowing where these benchmarks are on the number line helps us estimate where other fractions belong. For example:
Example: Where would 3/8 be? Since 3/8 is less than 1/2 (4/8) and greater than 1/4 (2/8), it would be between 1/4 and 1/2 on the number line.
Practice Tip
Draw number lines and practice placing different fractions between the benchmark points.
Comparing Fractions Using Benchmarks
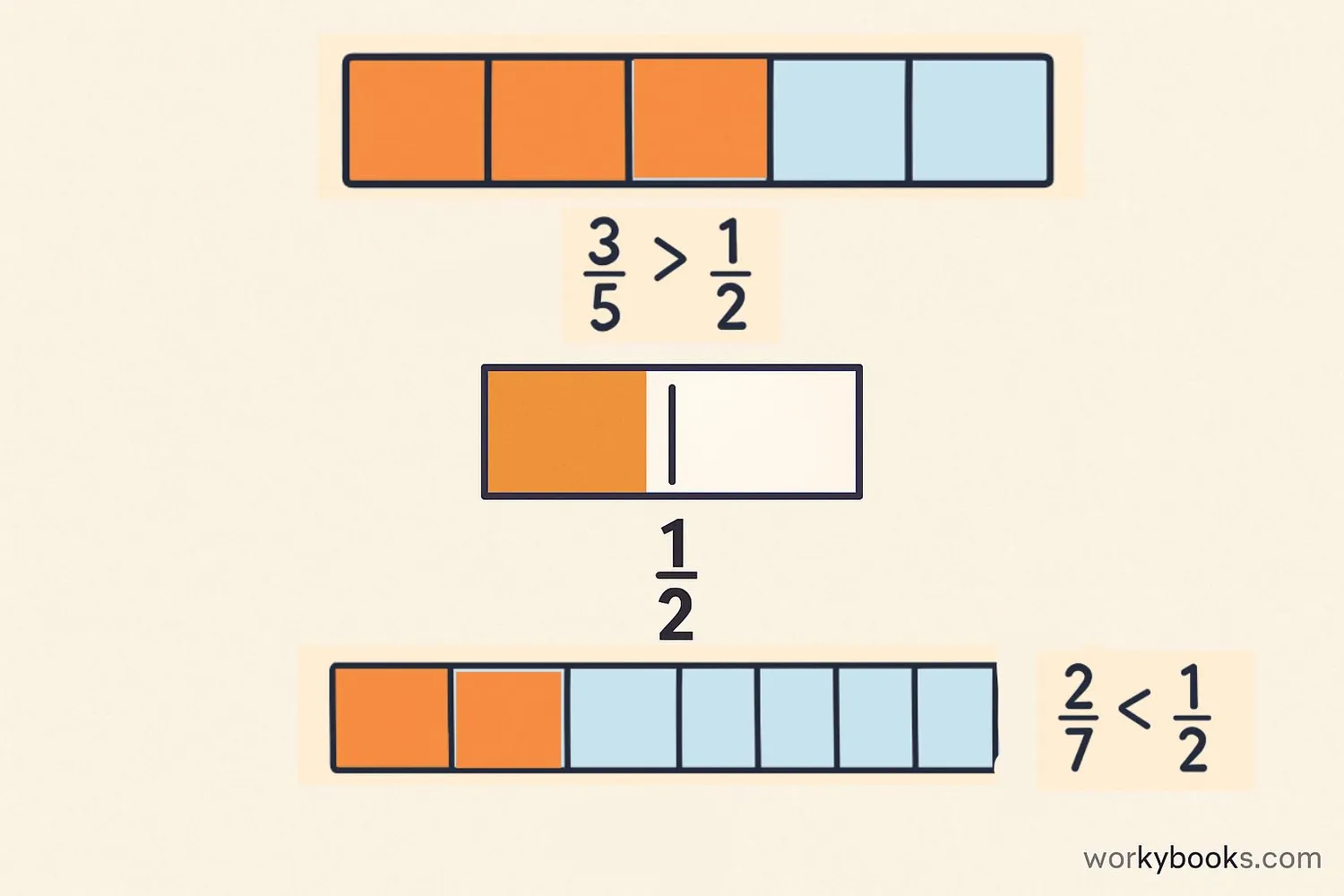
Benchmark fractions are especially helpful when we need to compare two fractions. Instead of finding a common denominator, we can use our benchmarks as reference points.
How to compare fractions using benchmarks:
- Identify the benchmark fractions (0, 1/2, 1)
- Determine if each fraction is less than, greater than, or equal to 1/2
- Compare the fractions based on their relationship to 1/2
Example 1: Compare 3/5 and 2/7
3/5 is greater than 1/2 (since 1/2 = 2.5/5)
2/7 is less than 1/2 (since 1/2 = 3.5/7)
Therefore, 3/5 > 2/7
Example 2: Compare 5/8 and 3/4
Both are greater than 1/2
5/8 is a little more than 1/2 (4/8)
3/4 is equal to 6/8, which is more than 5/8
Therefore, 5/8 < 3/4
With practice, you'll be able to compare fractions quickly using these benchmarks!
Comparison Tip
When both fractions are on the same side of 1/2, compare them to other benchmarks like 1/4 or 3/4 for more precision.
Benchmark Fractions Practice Quiz
Test your understanding of benchmark fractions with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about benchmark fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they only used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fraction Origins
The word "fraction" comes from the Latin word "fractio" which means "to break." This makes sense because fractions represent broken or divided parts of a whole.
Fractions in Nature
Fractions appear everywhere in nature! The patterns on seashells often follow fractional sequences, and the way leaves grow on stems frequently follows fractional patterns called phyllotaxis.
Fraction Records
The fraction with the longest terms is 1/982,451,653. But the most commonly used fractions in everyday life are 1/2, 1/4, and 1/3 - our benchmark fractions!





