Binary Multiplication - Definition, Examples, Quiz, FAQ, Trivia
Learn to multiply binary numbers with simple explanations, examples, and interactive activities
What is Binary Multiplication?
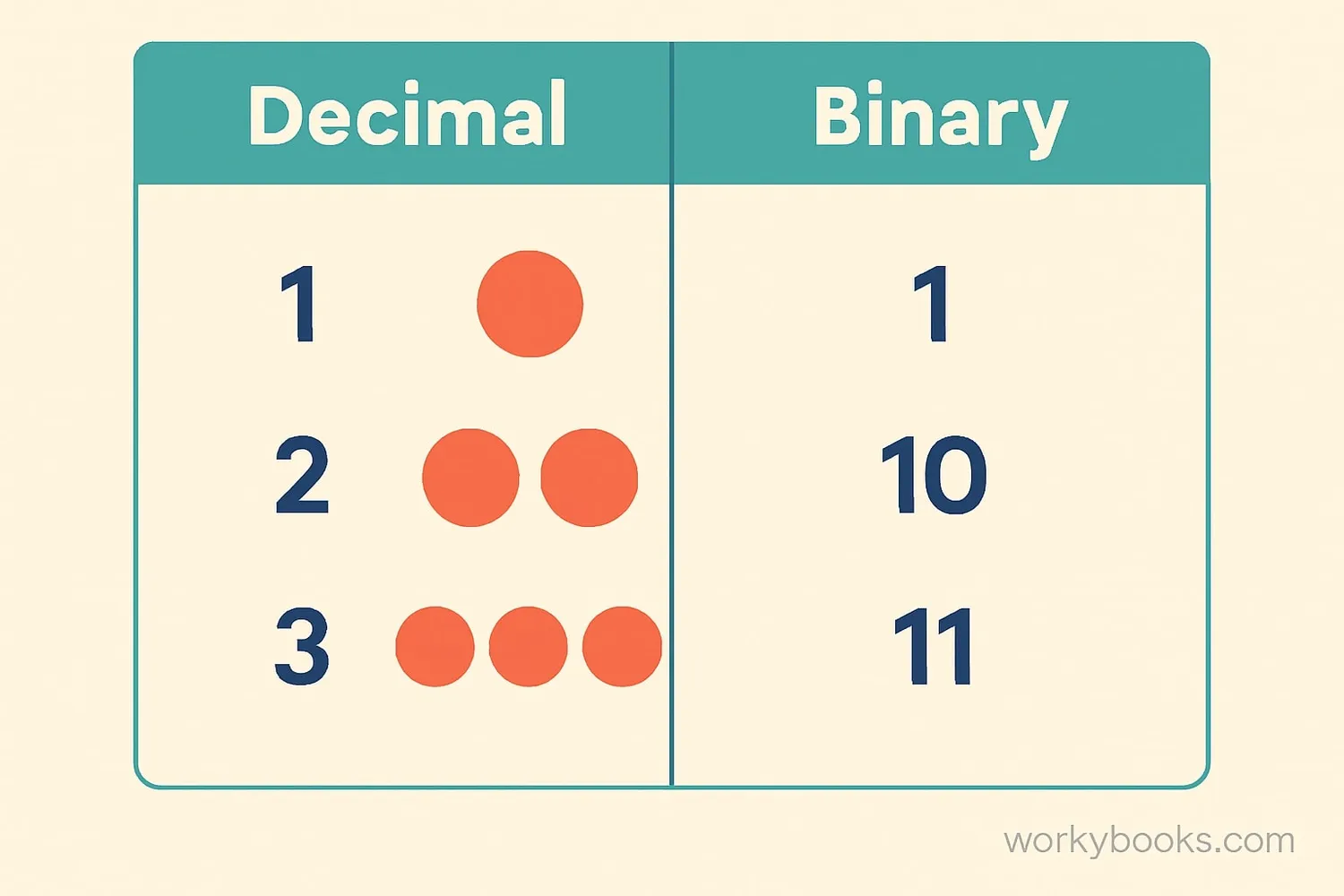
Binary multiplication is multiplying two binary numbers. Binary numbers are base-2 numbers that use only two digits: 0 and 1. This is different from our regular decimal system that uses ten digits (0-9).
Why learn binary? Computers use binary numbers to process information because they work with electrical signals that can be either on (1) or off (0). Learning binary multiplication helps us understand how computers perform calculations.
Binary multiplication works similarly to decimal multiplication but is actually simpler because you only work with two digits. The key is understanding the basic rules of multiplying 0s and 1s.
Key Concept
Binary means "two" - binary numbers use only two digits: 0 and 1.
Binary Multiplication Rules
Binary multiplication has only four simple rules to remember. These rules are much simpler than the multiplication tables we use in decimal!
| First Number | Second Number | Result |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Notice that:
- Multiplying by 0 always gives 0
- Multiplying by 1 gives the other number
- The only time you get 1 is when both numbers are 1
Remember
Binary multiplication rules are simpler than decimal because there are only four possible combinations!
How to Multiply Binary Numbers
Multiplying binary numbers is similar to multiplying decimal numbers, but simpler because we only use 0s and 1s. Let's multiply 101 (which is 5 in decimal) by 11 (which is 3 in decimal) step by step:
101
× 11
------
101
× 11
------
101 ← 101 × 1 (first digit)
101 ← 101 × 1 (second digit, shifted left)
------
101
+1010 ← Note the extra zero for shifting
------
1111
Tip
When adding binary numbers, remember that 1 + 1 = 10 (write 0, carry 1 to the next column).
Examples of Binary Multiplication
Let's look at more examples of binary multiplication:
Example 1: Multiply 10 (2 in decimal) by 10 (2 in decimal)
10
× 10
----
00 ← 10 × 0
10 ← 10 × 1 (shifted left)
----
100 ← Result (4 in decimal)
2 × 2 = 4, and 100 in binary is 4 in decimal.
Example 2: Multiply 111 (7 in decimal) by 101 (5 in decimal)
111
× 101
------
111 ← 111 × 1
000 ← 111 × 0 (shifted left)
111 ← 111 × 1 (shifted left two positions)
------
100011 ← Result (35 in decimal)
7 × 5 = 35, and 100011 in binary is 32 + 2 + 1 = 35 in decimal.
Practice Tip
Try converting your multiplication problems to binary, solve them, then convert back to decimal to check your work!
Binary Multiplication Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about binary multiplication:
Binary Trivia
Discover interesting facts about binary numbers and computer math:
Ancient Origins
The binary number system was first described by ancient Indian mathematician Pingala in the 3rd century BCE! He used it for classifying poetic meters.
Computer Brains
A modern computer processor can perform billions of binary multiplications in a single second. That's faster than you can blink!
Space Exploration
All spacecraft use binary numbers to communicate with Earth. The Voyager spacecraft, now in interstellar space, still sends binary data back to NASA.
Human Calculation
The world record for multiplying two 13-digit binary numbers is held by Alexis Lemaire, who did it in his head in just 0.8 seconds!





