Bisect - Definition, Examples, Quiz, FAQ, Trivia

What Does Bisect Mean?

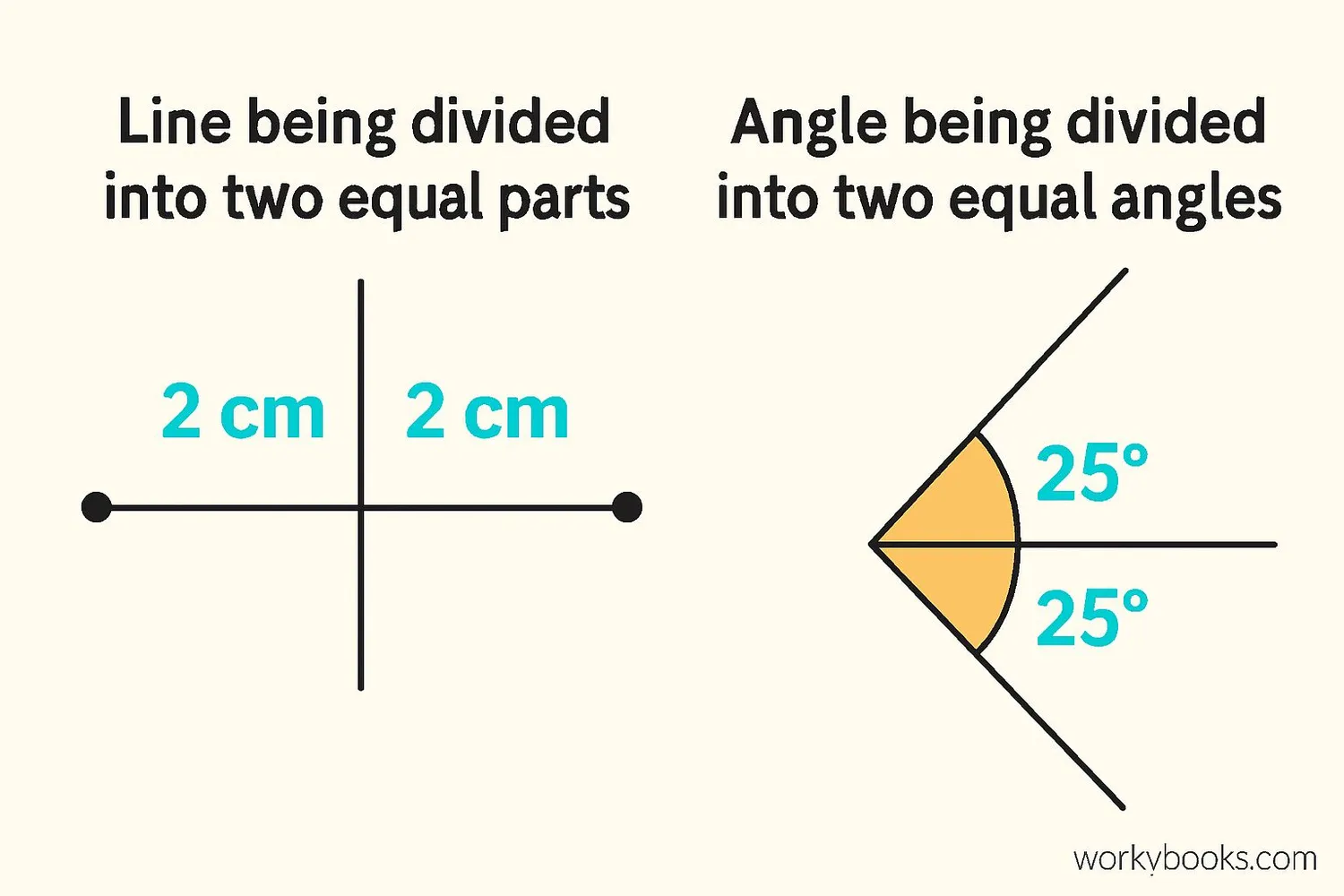
Bisect means to divide something into two equal parts. In geometry, we can bisect lines, angles, and shapes. When we bisect something, we create two parts that are exactly the same size and shape.

Think about cutting a sandwich in half - if you cut it perfectly down the middle so both pieces are equal, you've bisected the sandwich! In geometry, we do this with lines and angles using special tools like a compass and straightedge.

There are two main types of bisectors in geometry:

• Angle bisector: A line that divides an angle into two equal angles
• Line segment bisector: A line that divides another line segment into two equal parts

Angle Bisector

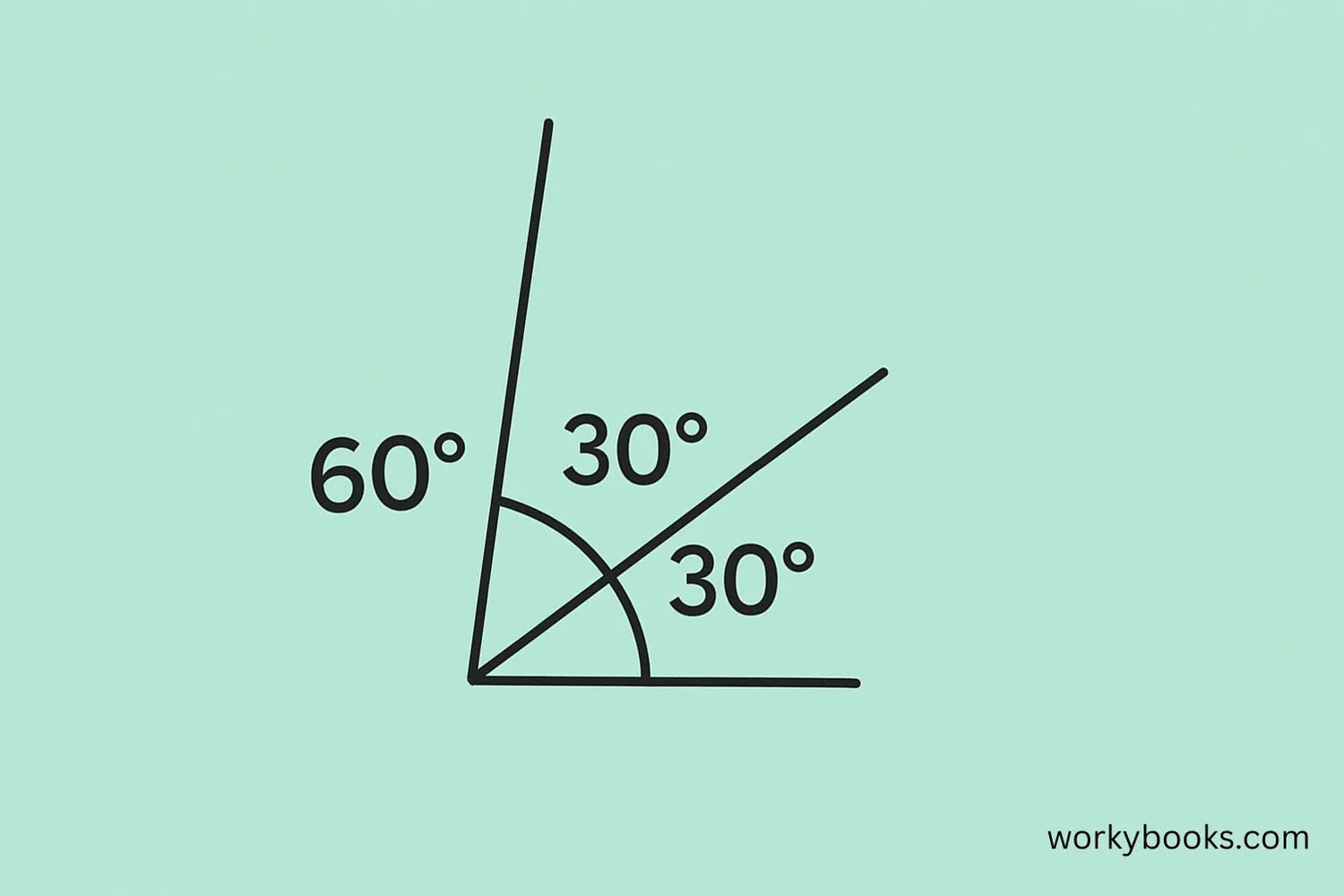
An angle bisector is a line that divides an angle into two equal smaller angles. If you have a 60° angle and draw an angle bisector, it will create two 30° angles.

1. Draw an angle with your straightedge
2. Place the compass at the angle's vertex and draw an arc that crosses both sides
3. From where the arc crosses each side, draw two new arcs that intersect
4. Draw a line from the vertex through this intersection point - this is your angle bisector!

Line Segment Bisector

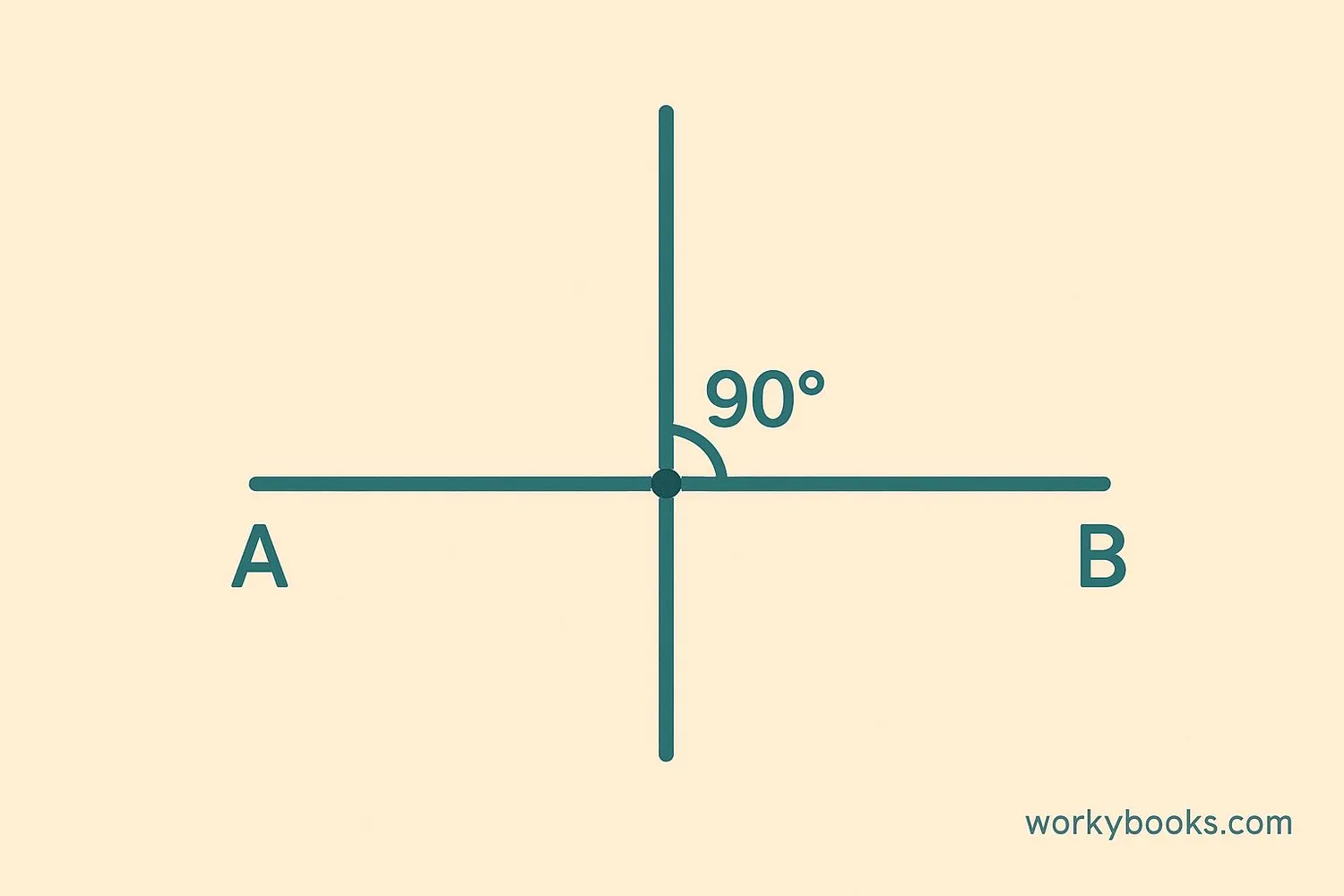
A line segment bisector is a line that divides another line segment into two equal parts. The most common type is the perpendicular bisector, which crosses the line segment at 90° (a right angle).

Properties of a perpendicular bisector:

• Divides the line segment into two equal lengths
• Forms right angles (90°) with the original line segment
• Every point on the perpendicular bisector is equally distant from both ends of the line segment

1. Draw your line segment with a straightedge
2. Set your compass to more than half the segment's length
3. Draw arcs from both ends that intersect above and below the line
4. Connect these intersection points - this is your perpendicular bisector!

Real-World Examples

Bisectors appear in many everyday objects and situations:

Example 1: When you fold a piece of paper perfectly in half, the crease is a line bisector.

Example 2: The line down the middle of a football field is a perpendicular bisector - it divides the field into two equal halves.

Example 3: The angle bisector of a clock at 3:00 would point at 1:30 - dividing the 90° angle between 12 and 3 into two 45° angles.

Example 4: In architecture, bisectors help create symmetrical designs. The Taj Mahal's design uses many bisectors to create perfect symmetry.

Example 5: When you cut an apple exactly in half through the core, you've created a bisector of the apple!

Try finding bisectors in your environment - in furniture, buildings, or even nature!

Bisector Practice Quiz

Test your understanding with this 5-question quiz. Choose the correct answer for each question.

Frequently Asked Questions

Here are answers to common questions about bisectors:

Geometry Trivia

Discover interesting facts about bisectors and geometry: