Boolean - Definition, Examples, Quiz, FAQ, Trivia
Learn about true/false logic with simple explanations, examples, and practice activities
What is Boolean Algebra?

Boolean algebra is a special kind of math that uses only two values: true (1) and false (0). It's named after George Boole, who invented it in 1854.
Think of it like answering yes/no questions or turning switches on/off. Computers use Boolean algebra to make decisions and solve problems using these simple true/false values.
Examples:
- Is the light on? (Yes/No)
- Is this number greater than 5? (True/False)
- Is the door locked? (1/0)
Key Concept
Boolean algebra uses only two values: true (1) and false (0). Everything in computer logic builds from this simple idea.
Boolean Operators
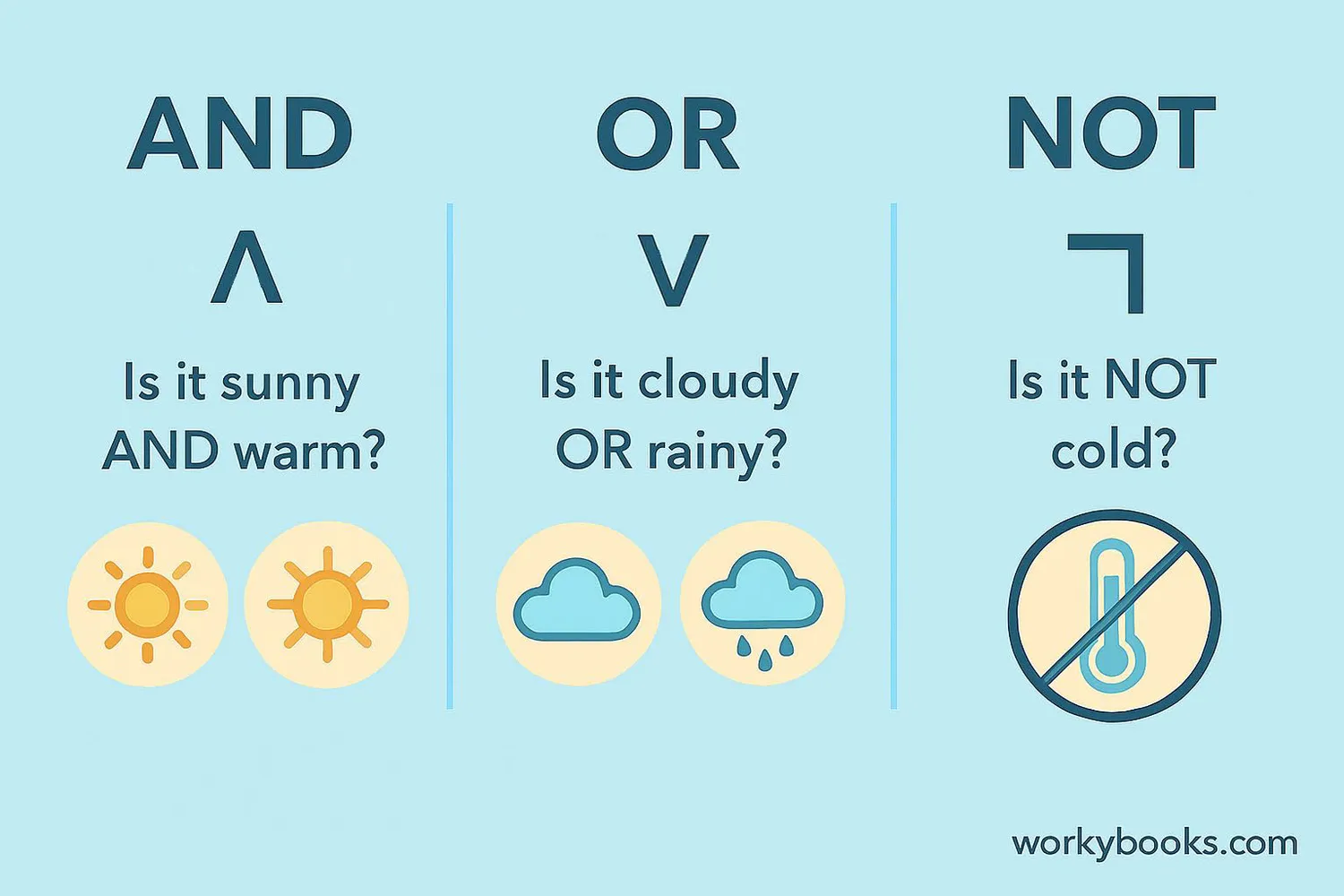
Boolean operators are special words that combine true/false values. The three basic operators are:
Basic Boolean Operators
These operators combine or change true/false values in specific ways
"Is it sunny AND warm?" → Only true if both are true
OR (at least one true):
"Is it raining OR snowing?" → True if either is true
NOT (changes true to false and vice versa):
"Is the door NOT locked?" → Changes the value to its opposite
Boolean Operator Examples
| Operator | Symbol | Example | Result |
|---|---|---|---|
| AND | ∧ | True ∧ False | False |
| OR | ∨ | True ∨ False | True |
| NOT | ¬ | ¬True | False |
Remember
AND is like multiplication (0 × 1 = 0), OR is like addition (but 1 + 1 = 1), and NOT flips the value.
Logic Gates
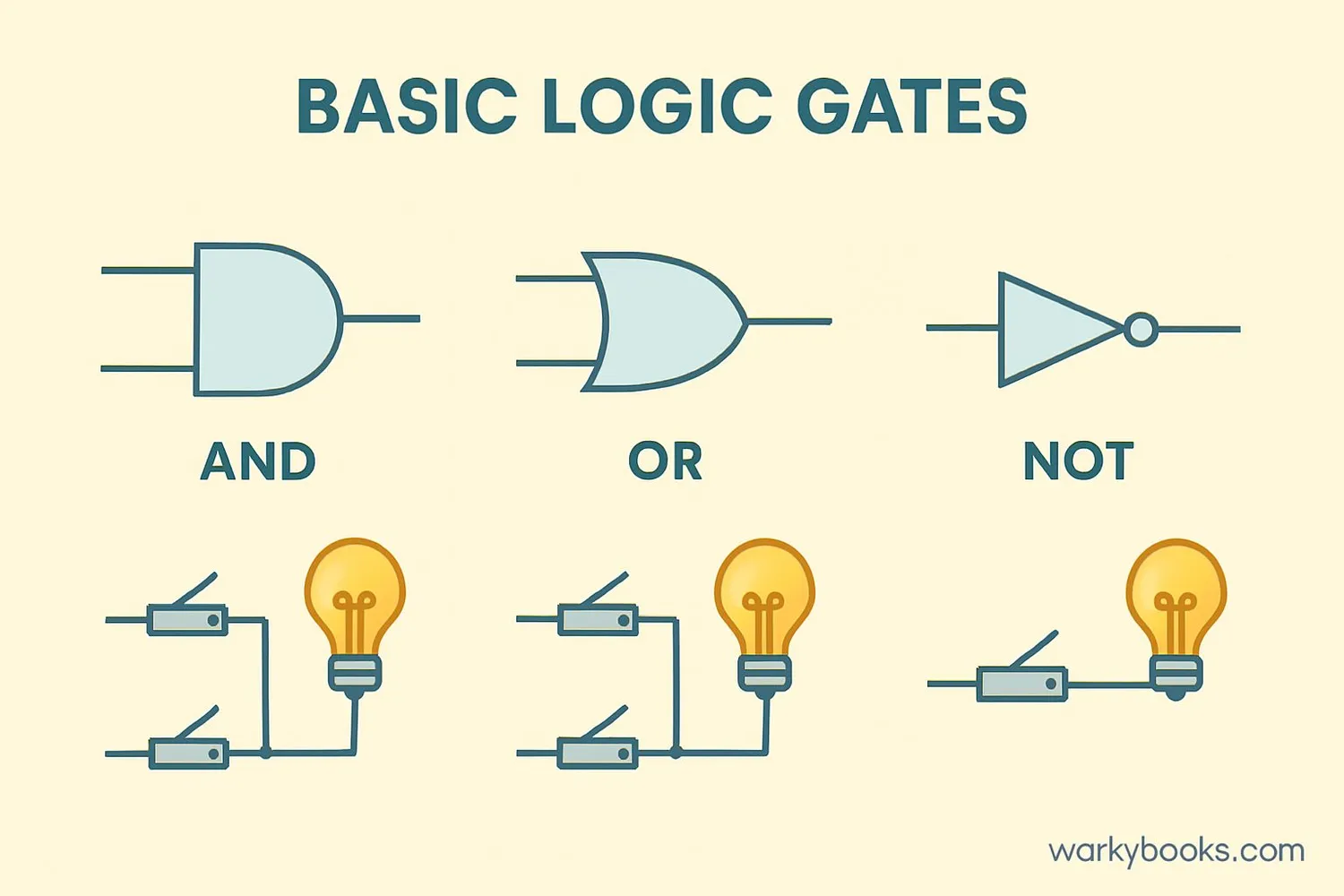
Logic gates are tiny electronic components that perform Boolean operations. They're the building blocks of computers! Each gate takes one or more inputs (true/false) and gives one output based on its operation.
AND Gate: Output is true only if all inputs are true
OR Gate: Output is true if any input is true
NOT Gate: Output is the opposite of the input
Computers combine millions of these tiny gates to perform all their calculations and make decisions.
Common Logic Gates
| Gate | Symbol | Input A | Input B | Output |
|---|---|---|---|---|
| AND | AND symbol | 0 | 0 | 0 |
| AND | AND symbol | 1 | 0 | 0 |
| AND | AND symbol | 1 | 1 | 1 |
| OR | OR symbol | 0 | 0 | 0 |
| OR | OR symbol | 1 | 0 | 1 |
| OR | OR symbol | 1 | 1 | 1 |
| NOT | NOT symbol | 0 | - | 1 |
| NOT | NOT symbol | 1 | - | 0 |
Did You Know?
A smartphone contains billions of logic gates working together to run apps, play games, and connect to the internet!
Truth Tables
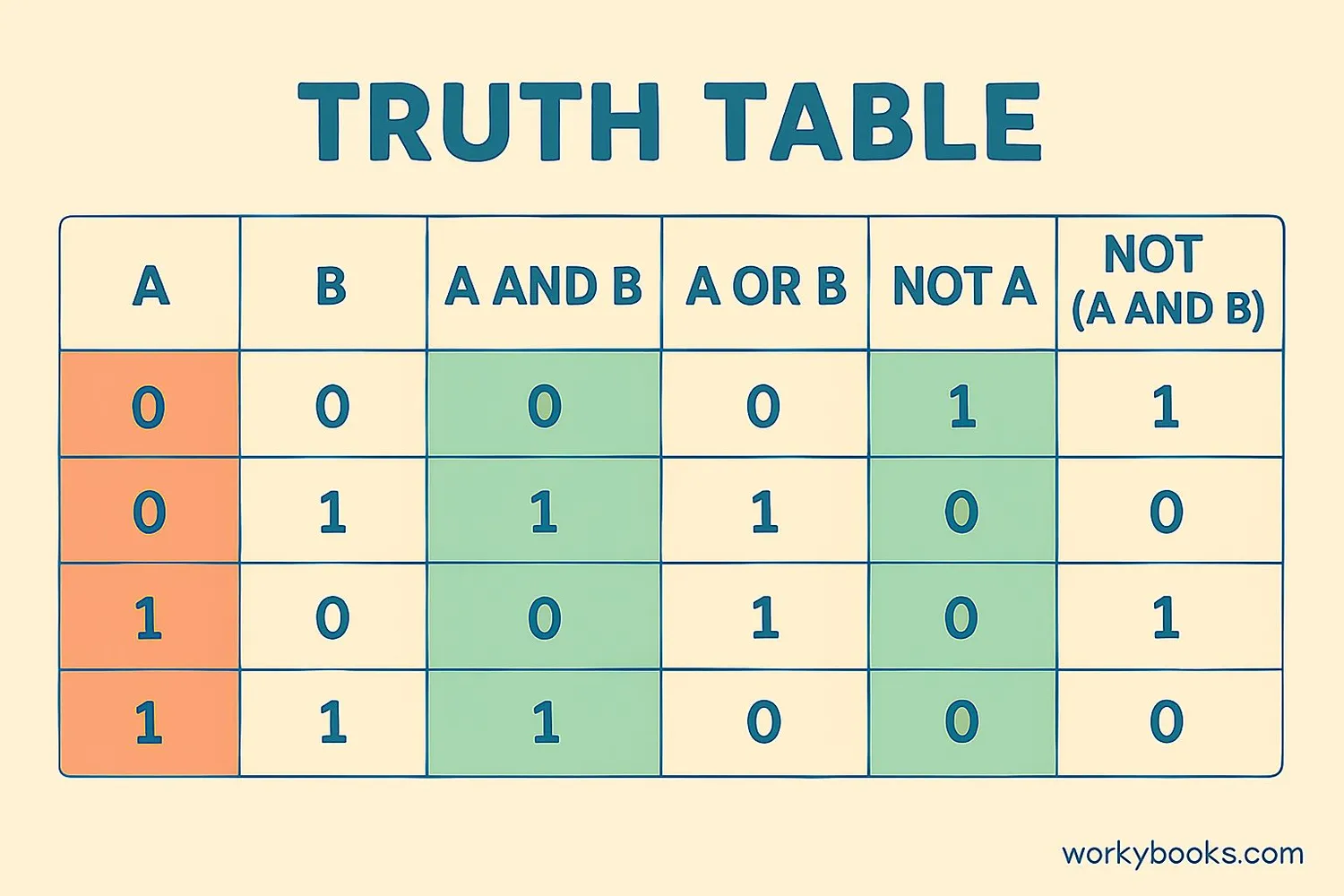
A truth table shows all possible inputs and their corresponding outputs for a Boolean operation. It's like a multiplication table but for true/false values.
For operations with two inputs (like AND and OR), there are four possible combinations (2 × 2). For NOT (one input), there are two possibilities.
Truth tables help us understand how Boolean operations work by showing every possible case. Here's the complete truth table for basic operations:
Complete Truth Table
| A | B | A AND B | A OR B | NOT A |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
Table Tip
Notice how AND only has one "1" (when both inputs are 1), while OR has three "1"s (only false when both inputs are 0).
Boolean Algebra Quiz
Test your understanding with this 5-question quiz about Boolean concepts:
Frequently Asked Questions
Here are answers to common questions about Boolean algebra:
Logic Trivia
Discover interesting facts about Boolean logic and computing:
Boolean's Legacy
George Boole's work was so important that we name digital concepts after him: Boolean algebra, Boolean logic, Boolean operators, and even the data type "boolean" in programming languages!
Tiny Logic
A modern computer chip contains billions of logic gates. The Apple M1 chip has about 16 billion transistors, each helping to form logic gates that perform calculations.
Moon Landing
The Apollo Guidance Computer that landed humans on the moon used about 5,600 NOR gates (a type of logic gate) to perform all its calculations with very little memory.
All From Three
Every possible logic operation can be built using just NAND gates or just NOR gates. This means all computer calculations can be done with just one type of gate repeated millions of times!




