Centroid of a Triangle - Definition, Examples, Quiz, FAQ, Trivia
Discover the balancing point of triangles with easy explanations and interactive activities
What is the Centroid of a Triangle?
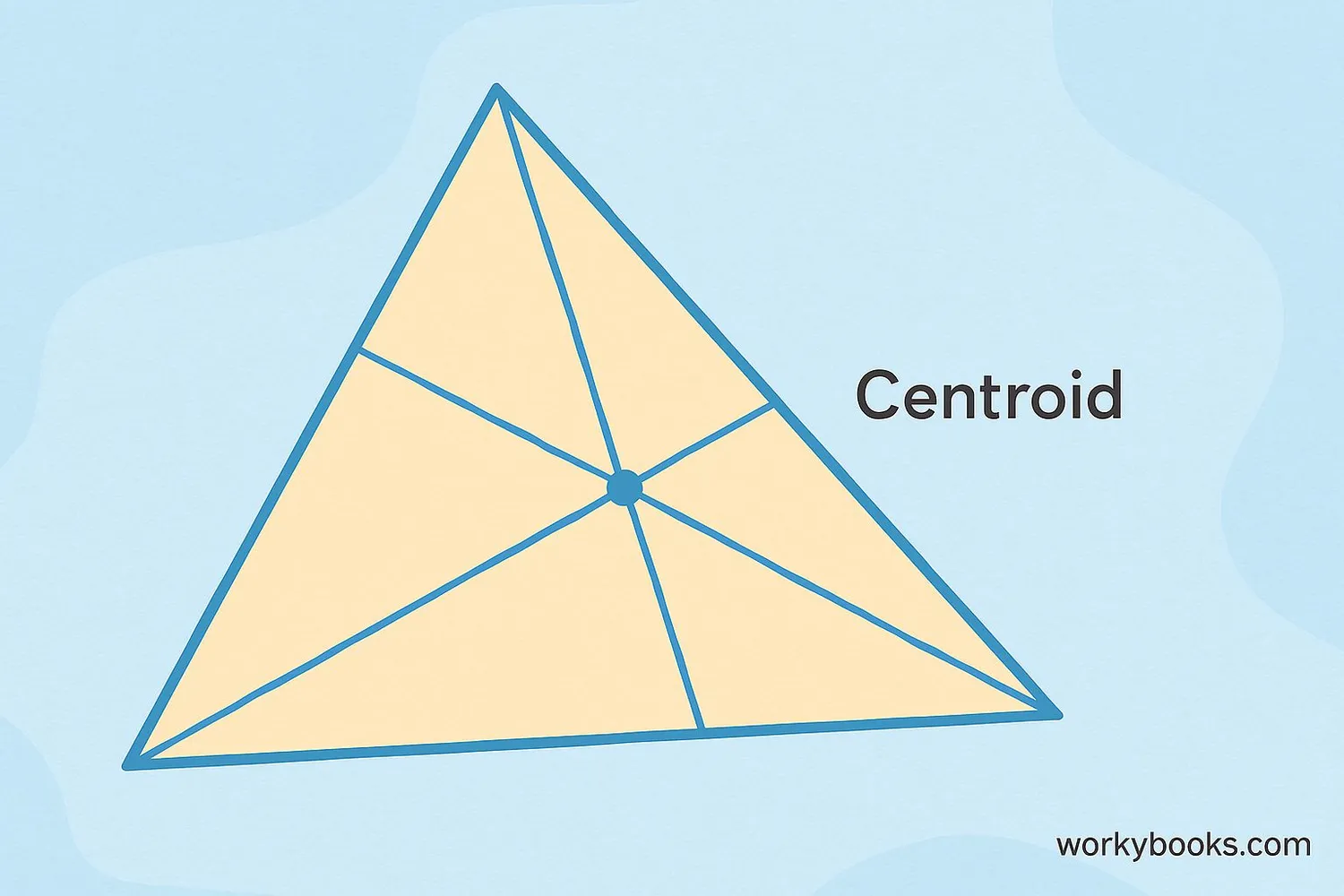
The centroid is the point where all three medians of a triangle intersect. But what's a median? A median is a line segment that connects a vertex (corner point) of a triangle to the midpoint of the opposite side.
Think of the centroid as the balancing point of the triangle. If you could cut out a triangle from cardboard, the centroid is exactly where you could balance it perfectly on the tip of your finger!
Every triangle has exactly one centroid, and it's always located inside the triangle, regardless of the triangle's shape (acute, obtuse, or right-angled).
Key Concept
The centroid is the point where the three medians of a triangle meet. It's also the center of gravity (balance point) of the triangle.
How to Find the Centroid
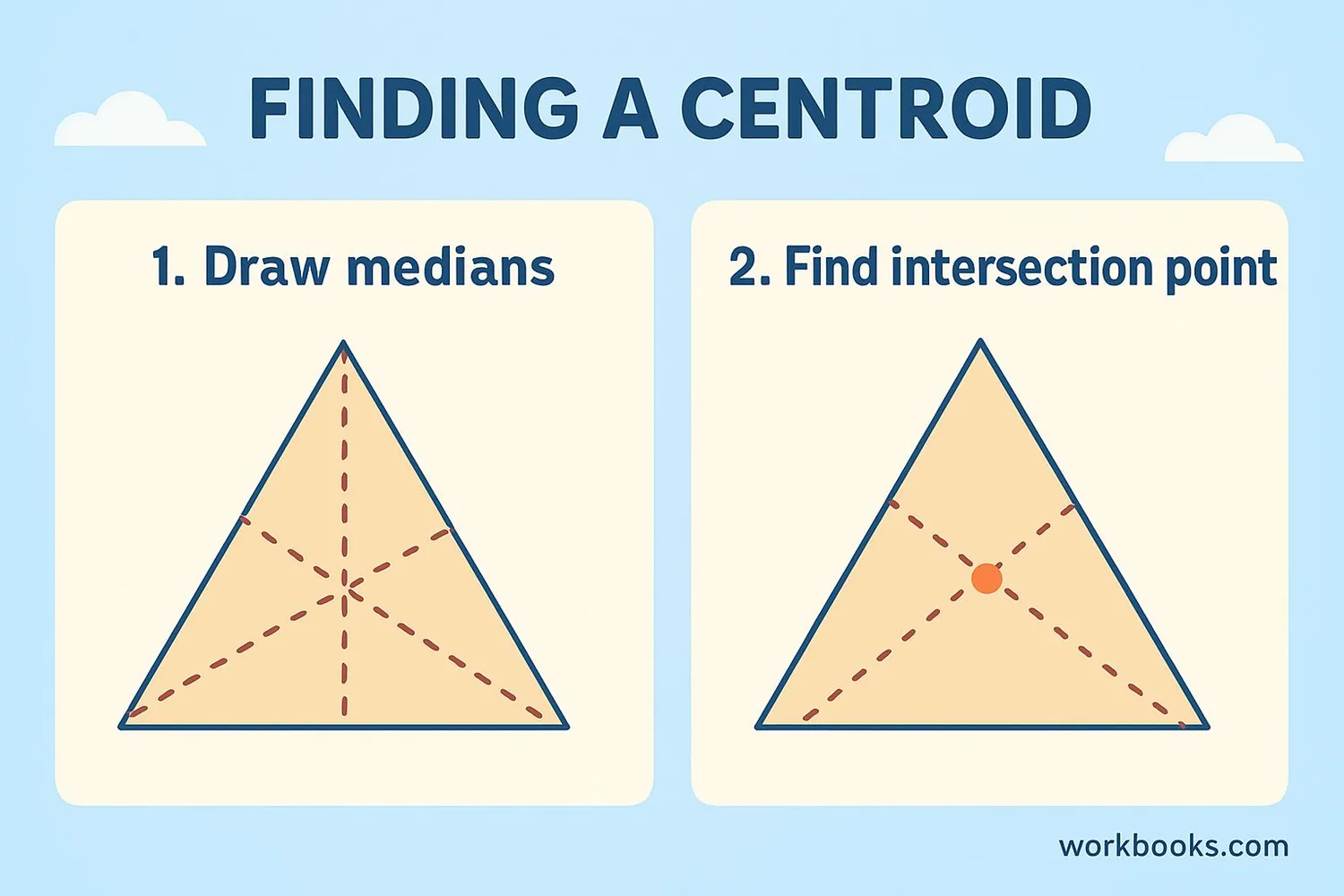
There are two main ways to find the centroid of a triangle:
1. Using Geometry (Ruler Method):
- Find the midpoint of each side of the triangle
- Draw a line segment (median) from each vertex to the midpoint of the opposite side
- The point where all three medians intersect is the centroid
Centroid Formula
Where (x₁,y₁), (x₂,y₂), (x₃,y₃) are the coordinates of the triangle's vertices
Solution:
x-coordinate: (1 + 3 + 5)/3 = 9/3 = 3
y-coordinate: (2 + 4 + 0)/3 = 6/3 = 2
Centroid is at (3,2)
Remember
Each median is divided by the centroid in a 2:1 ratio, with the longer part closer to the vertex.
Properties of the Centroid
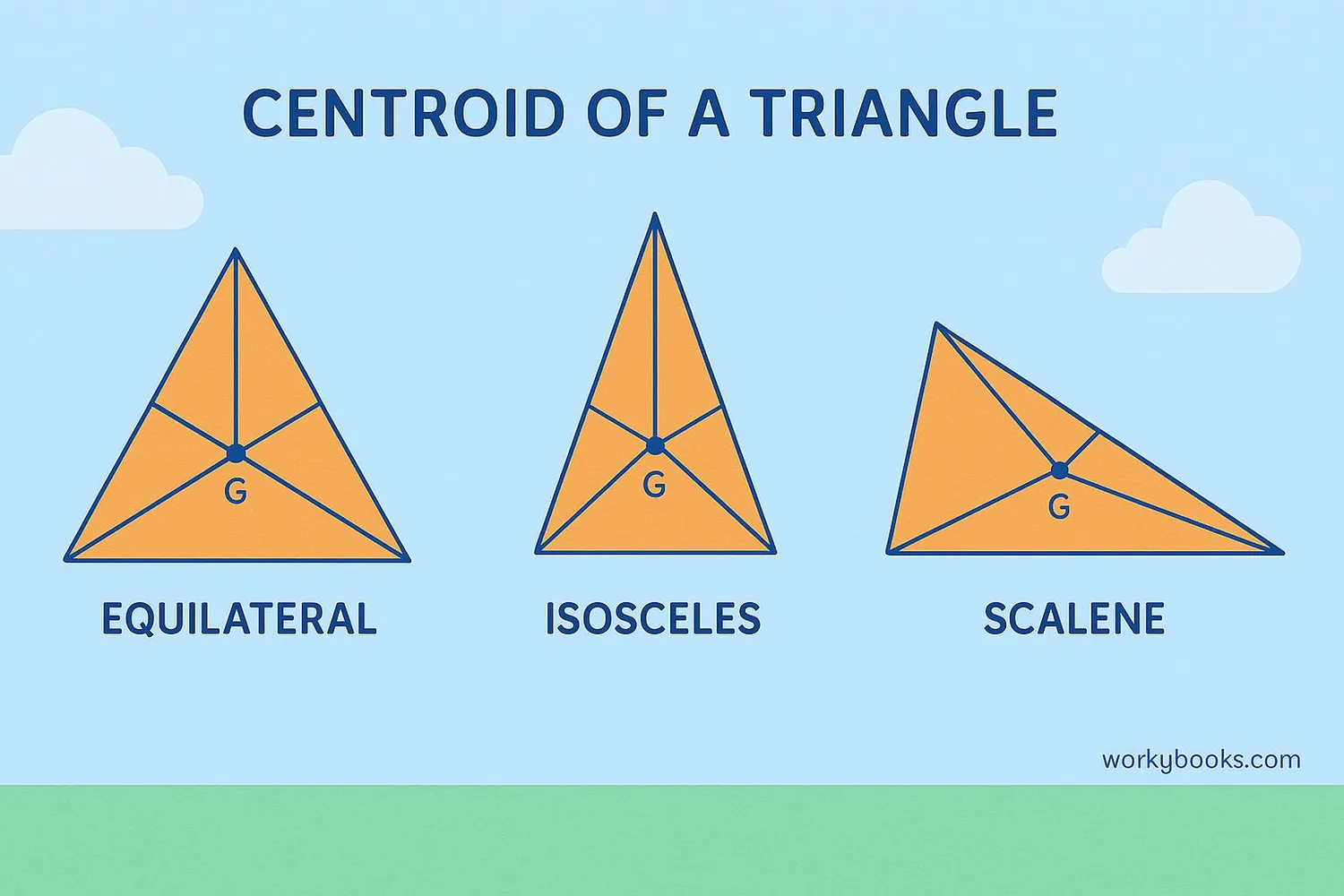
The centroid has some special properties that are true for all triangles:
1. Balancing Point: The centroid is the center of gravity of the triangle. This means it's the balance point where the triangle would be perfectly balanced.
2. Median Divider: The centroid divides each median into two segments with a 2:1 ratio. The segment from the vertex to the centroid is twice as long as the segment from the centroid to the midpoint.
3. Always Inside: No matter what type of triangle you have (acute, right, or obtuse), the centroid will always be located inside the triangle.
4. Coordinate Average: As shown in the formula, the centroid's coordinates are the average of the coordinates of the three vertices.
5. Equal Area Divider: The three smaller triangles formed by connecting the centroid to the vertices all have equal area.
Special Note
In an equilateral triangle (where all sides are equal), the centroid, circumcenter, orthocenter, and incenter all coincide at the same point!
Real-World Examples
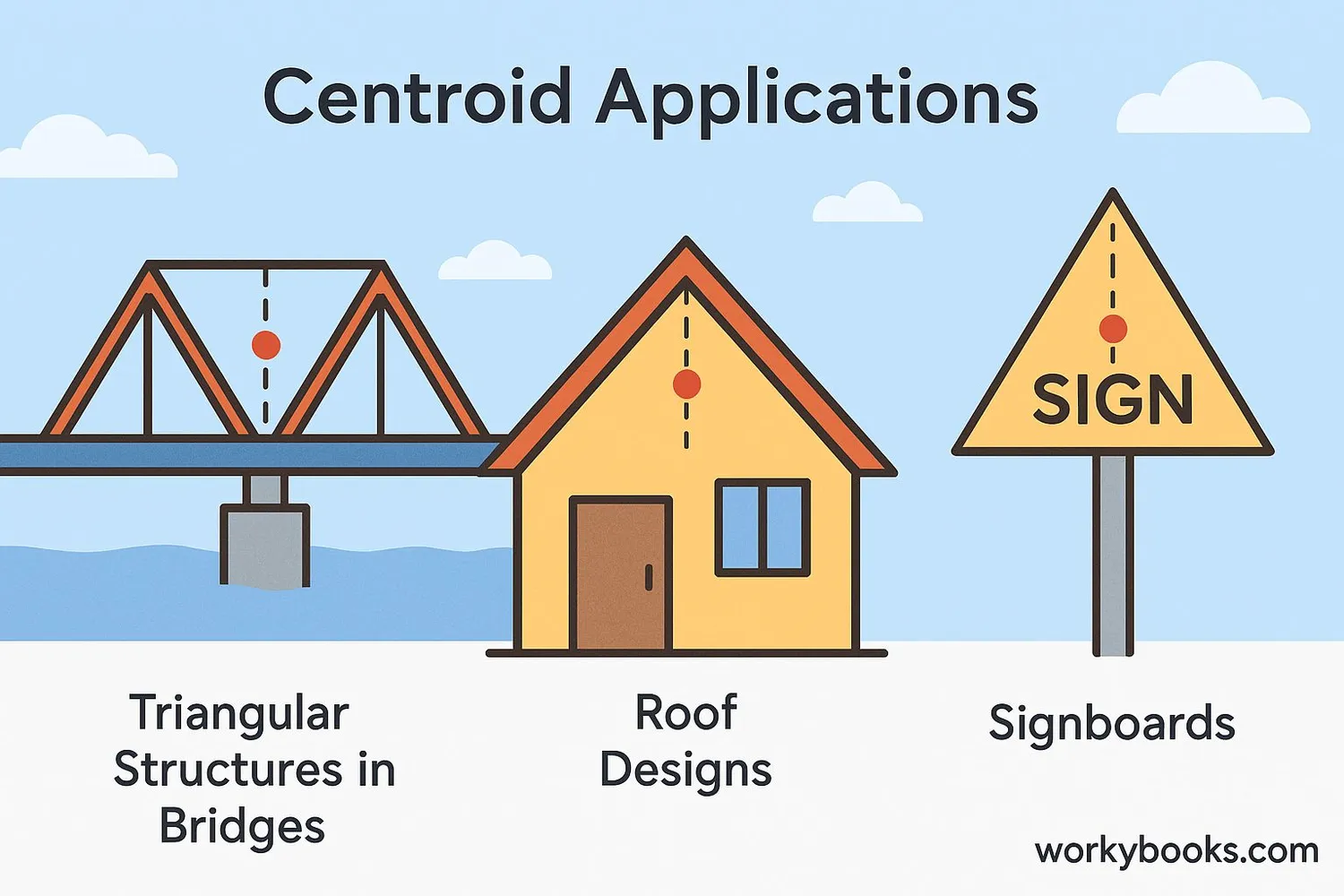
Understanding centroids helps us in many real-world applications:
Example 1: Architecture
Architects use centroids when designing triangular structures like roofs or bridges. The centroid helps determine where to place supports for maximum stability.
Example 2: Engineering
In aerospace engineering, the centroid of airplane wings and other components is calculated to ensure proper balance during flight.
Example 3: Art and Design
Artists sometimes use the centroid to find the visual center of triangular shapes in their compositions.
Example 4: Physics
When calculating how objects rotate or balance, physicists use the centroid to represent the center of mass.
Practice Problem: A triangular park has corners at (0,0), (30,0), and (15,40). Find the centroid where a fountain should be placed for perfect balance.
Solution:
x-coordinate: (0 + 30 + 15)/3 = 45/3 = 15
y-coordinate: (0 + 0 + 40)/3 = 40/3 ≈ 13.33
Centroid at (15, 13.33)
Try This
Draw a triangle on paper, find the midpoints, draw the medians, and locate the centroid. Then cut it out and try balancing it on your finger!
Centroid Quiz
Test your knowledge about centroids with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about triangle centroids:
Math Trivia
Discover interesting facts about geometry and centroids:
Ancient Discovery
The concept of the centroid was known to ancient Greek mathematicians. Archimedes (287-212 BC) used the centroid in his work on levers and centers of gravity.
Universal Balance
NASA calculates centroids for all spacecraft components. The centroid of the International Space Station determines how it rotates in space and how thrusters must fire to maintain position.
Nature's Geometry
Honeybees build honeycombs with hexagonal cells, but these hexagons are made from triangles! Bees instinctively create structures with centroids that provide maximum strength with minimal material.
Sports Science
In sports equipment design, the centroid is crucial. The "sweet spot" on a baseball bat or tennis racket is located near the centroid, where hitting the ball produces the least vibration in your hands.





