Circumference - Definition, Examples, Quiz, FAQ, Trivia
Learn about the distance around a circle with easy explanations, formulas, examples and quizzes
What is Circumference?
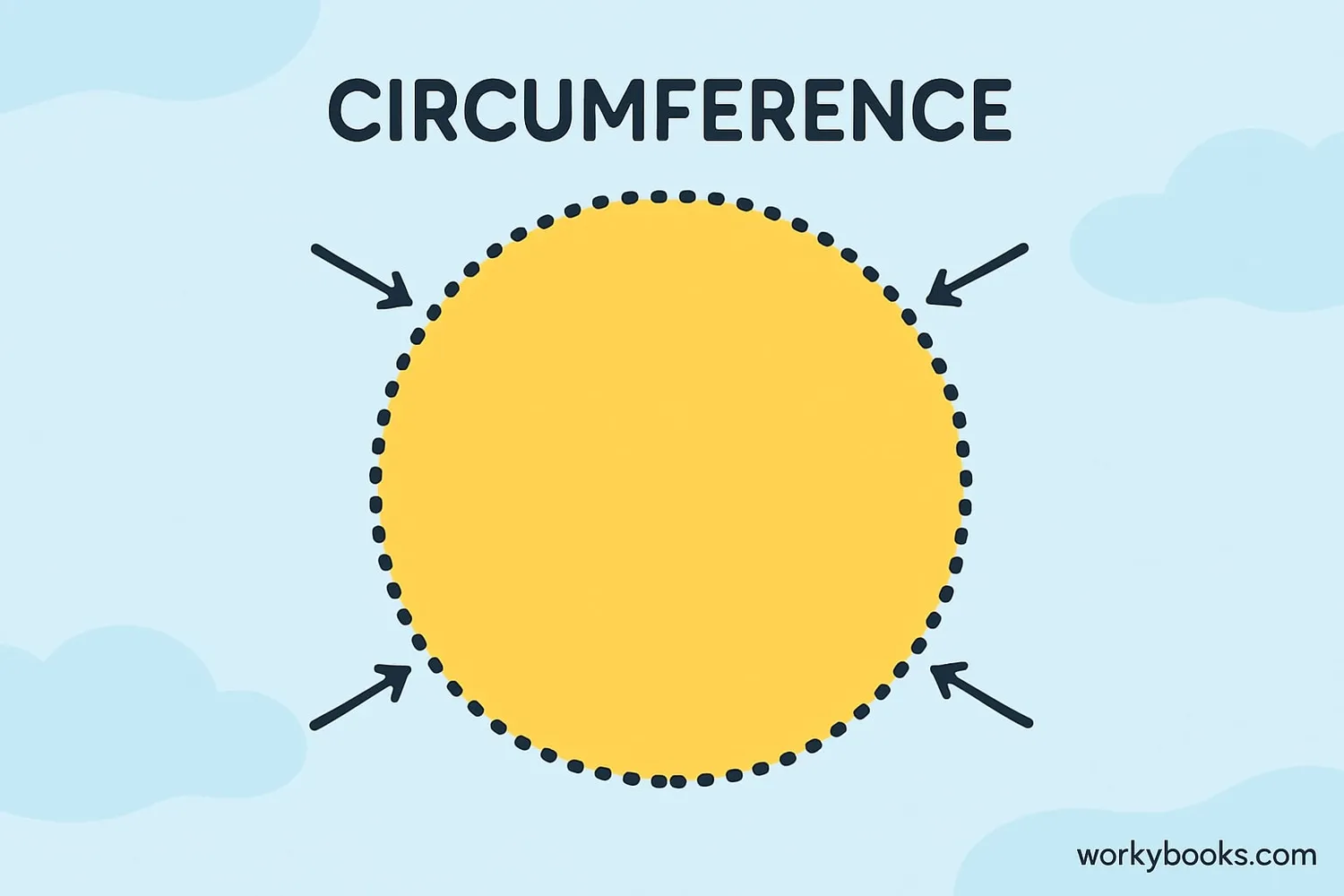
Circumference is the distance around a circle. It's similar to the perimeter of other shapes, but we use a special word for circles.
Think of it like this: If you took a string and wrapped it around a circle, the length of that string would be the circumference.
Circumference is important because it helps us understand how big circles are. We use this measurement for wheels, plates, clocks, and many other round objects in our daily lives.
The special thing about circles is that no matter how big or small they are, the relationship between the distance around (circumference) and the distance across (diameter) is always the same!
Key Concept
Circumference is the distance around a circle. It's the circle's perimeter.
The Circumference Formula
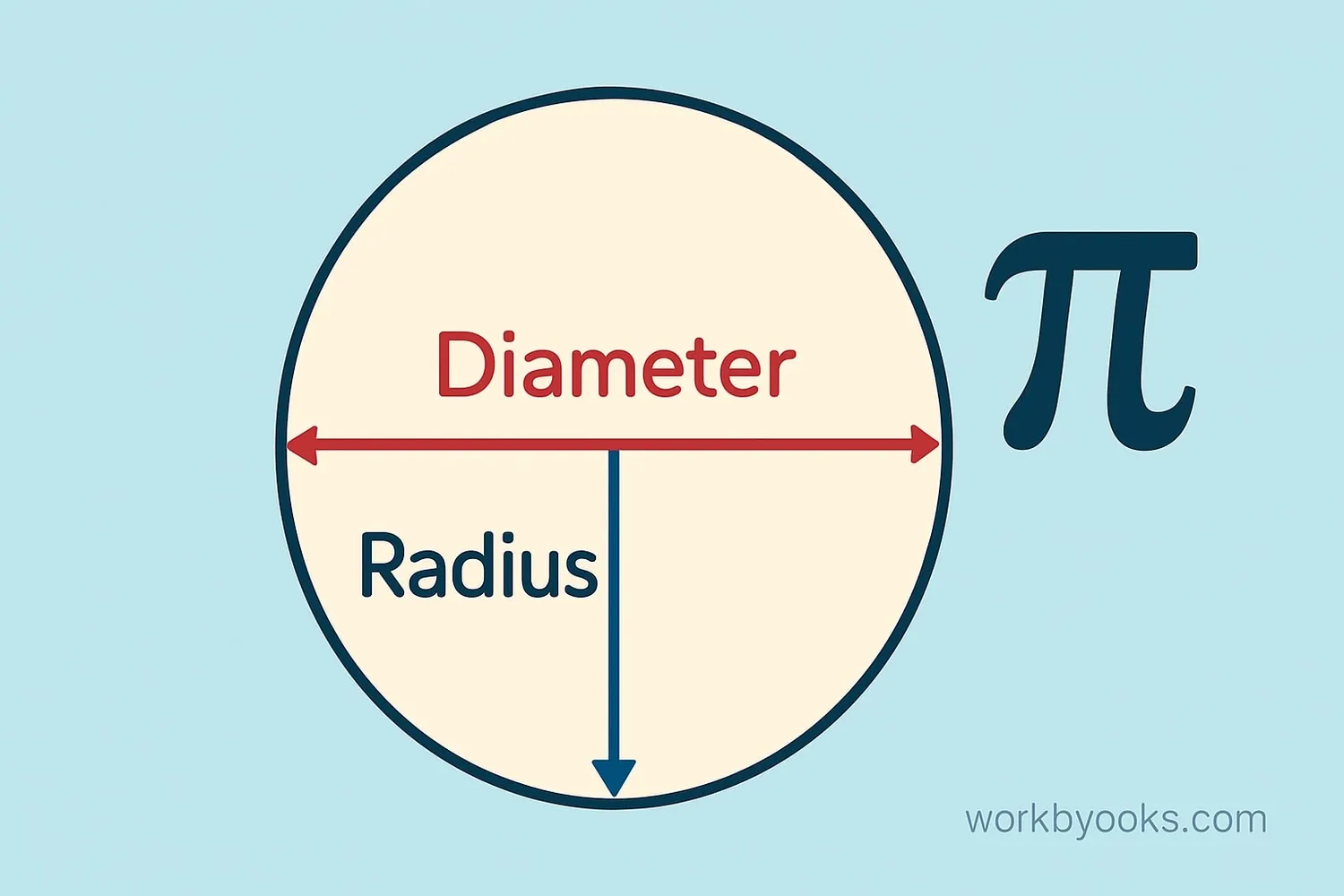
To calculate circumference, we use a special number called pi (pronounced "pie"). Pi is represented by the Greek letter π and is approximately equal to 3.14.
Pi is a mathematical constant that describes the relationship between a circle's circumference and its diameter. No matter how big or small the circle is, if you divide its circumference by its diameter, you always get pi!
We have two main formulas for circumference:
Circumference Formulas
Where C is circumference, π is pi (≈3.14), and d is diameter
Where r is the radius (half the diameter)
Remember
Diameter (d) is the distance across the circle through its center. Radius (r) is half the diameter.
How to Calculate Circumference
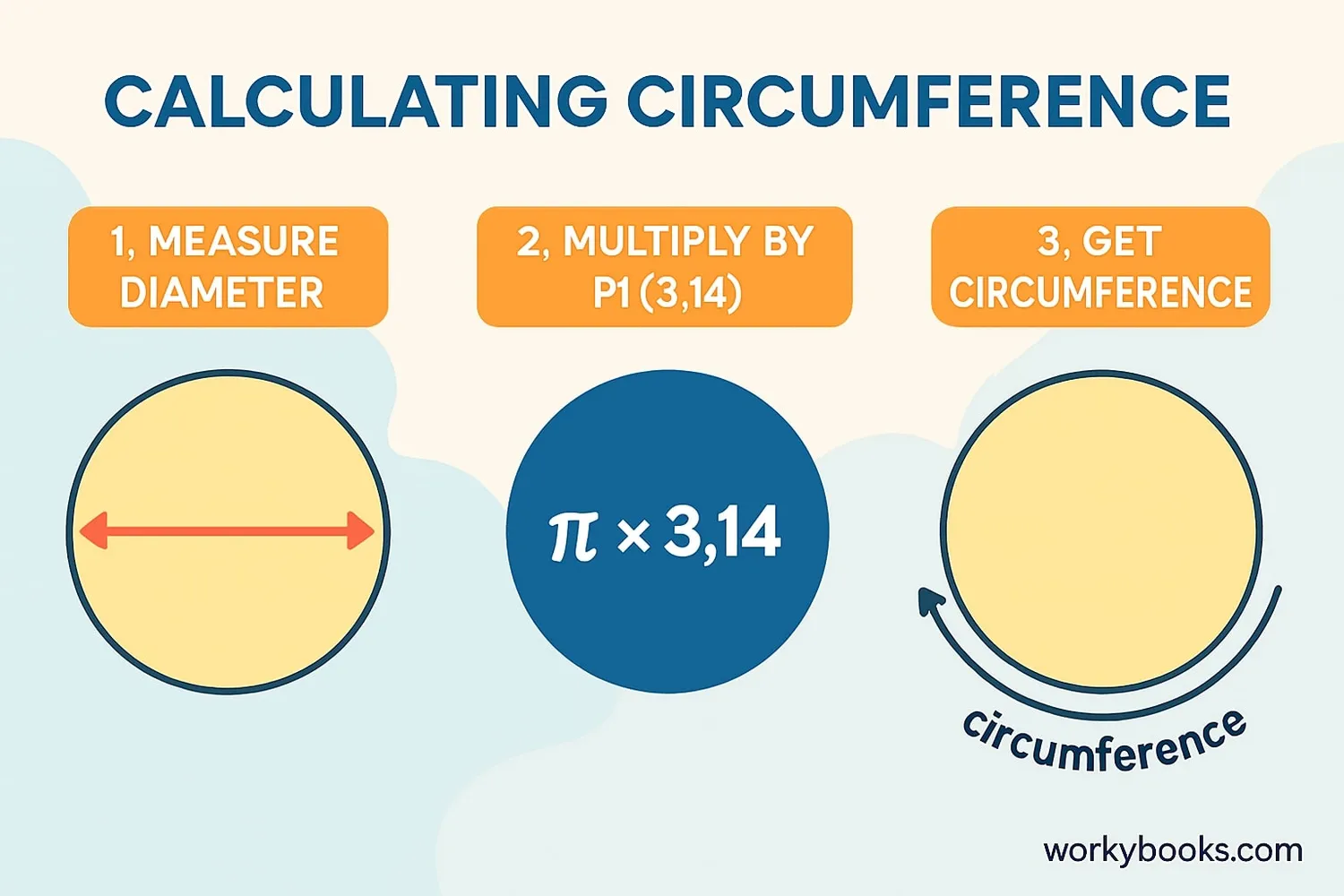
Let's walk through the steps to calculate circumference:
Step 1: Measure the diameter of the circle (distance across through the center)
Step 2: Multiply the diameter by pi (π ≈ 3.14)
Step 3: The result is the circumference!
If you only know the radius:
Step 1: Measure the radius (distance from center to edge)
Step 2: Multiply the radius by 2 to get the diameter
Step 3: Multiply the diameter by pi (π ≈ 3.14)
Or use the shortcut: Multiply the radius by 2 and then by pi (2 × π × r)
Calculation Tip
For most school work, using π ≈ 3.14 is accurate enough. For more precision, use 3.1416 or the π button on your calculator.
Real-World Examples

Let's practice with some real-world examples:
Example 1: A bicycle wheel has a diameter of 70 cm. What is its circumference?
Solution: C = π × d = 3.14 × 70 ≈ 219.8 cm
Example 2: A circular table has a radius of 1.5 meters. What is its circumference?
Solution: C = 2 × π × r = 2 × 3.14 × 1.5 ≈ 9.42 meters
Example 3: A circular running track has a circumference of 400 meters. What is its diameter?
Solution: d = C ÷ π = 400 ÷ 3.14 ≈ 127.4 meters
Example 4: A pizza has a diameter of 30 cm. What is the circumference of the pizza?
Solution: C = π × d = 3.14 × 30 ≈ 94.2 cm
Practice calculating circumference with circular objects around you - plates, wheels, coins, or lids!
Real-World Tip
Circumference is important for making tires, designing round buildings, creating circular tracks, and many engineering applications.
Circumference Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about circumference:
Math Trivia
Discover interesting facts about circles and circumference:
History of Pi
The concept of pi has been known for nearly 4,000 years! Ancient Babylonians calculated pi as 3.125, while Egyptians used 3.1605. The Greek mathematician Archimedes was the first to calculate pi theoretically.
Pi in Nature
Pi appears in many natural phenomena. The ripples from a raindrop in water form concentric circles whose circumference follows pi. Even the way rivers bend follows pi-related mathematics!
Pi in Space
NASA uses pi for space exploration! They use pi to calculate the orbits of planets, the surface area of asteroids, and the trajectory of spacecraft. Pi helps scientists explore the universe.
Pi World Record
The world record for memorizing pi digits is held by Rajveer Meena from India, who recited 70,000 decimal places! It took him over 10 hours while blindfolded. Most people only need 3.14 for everyday math.




