Circumference to Diameter - Definition, Examples, Quiz, FAQ, Trivia
Learn how circles work with easy explanations, formulas, and practice activities
Circle Basics: Circumference and Diameter

Every circle has two important measurements: circumference and diameter.
The circumference is the distance around the circle. If you took a string and wrapped it all the way around a circle, the length of that string would be the circumference.
The diameter is the distance across the circle through its center. It's the longest straight line you can draw from one side of the circle to the other.
These two measurements are always connected in a special way. No matter how big or small a circle is, the ratio between its circumference and diameter is always the same number!
Key Concept
Circumference = Distance around the circle
Diameter = Distance across the circle through its center
The Magic of Pi (π)

The special number that connects circumference and diameter is called pi (pronounced "pie"), and it's written with the Greek letter π.
Pi is approximately 3.14, but it actually goes on forever without repeating! Mathematicians have calculated over 50 trillion digits of pi, but we usually use 3.14 or the fraction 22/7 for calculations.
The relationship is simple:
Pi Formula
For any circle, if you divide its circumference by its diameter, you always get pi!
Remember
π ≈ 3.14 or 22/7. It's the same for every circle, no matter the size!
Circumference to Diameter Formula
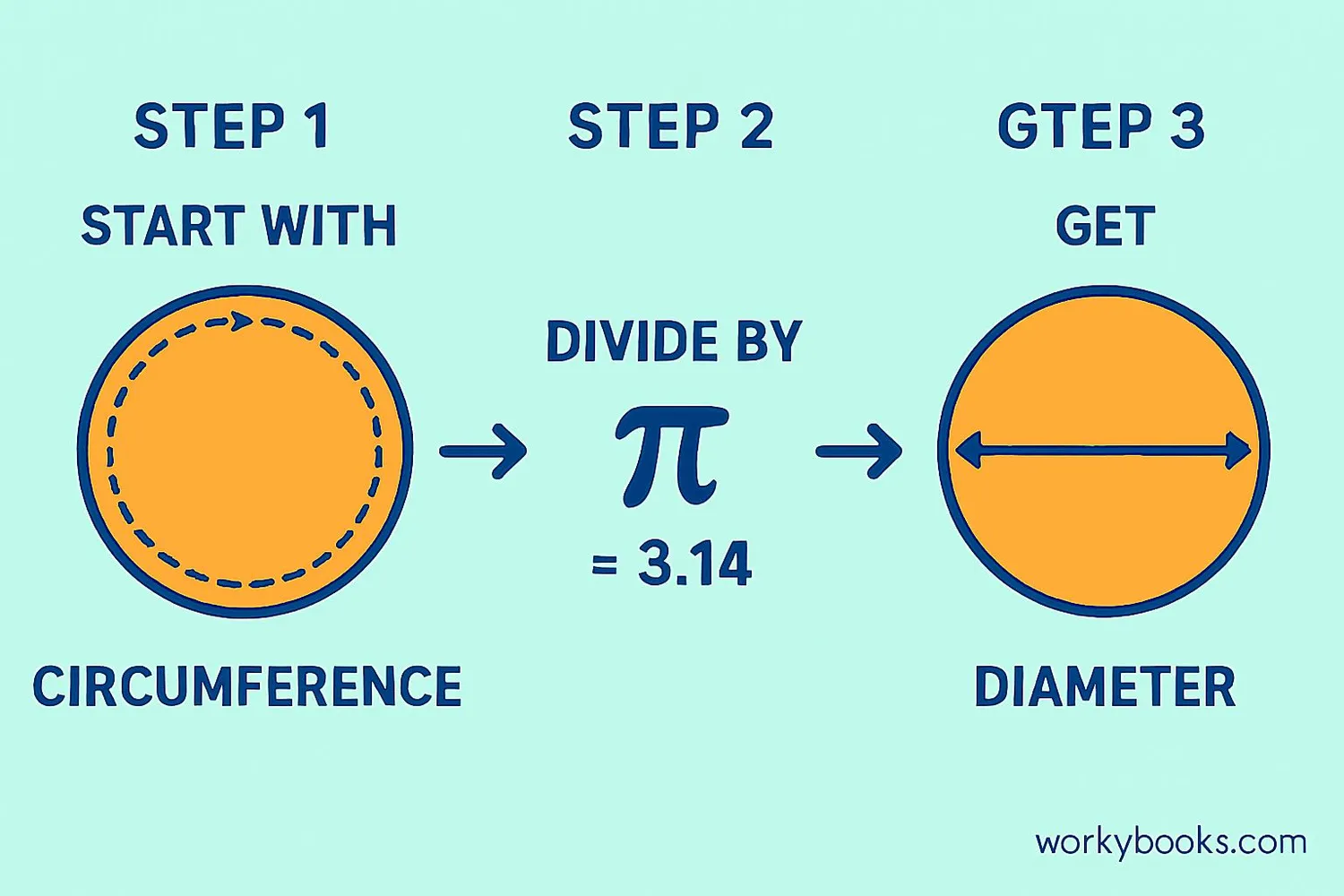
Since we know that π = Circumference ÷ Diameter, we can rearrange the formula to find the diameter when we know the circumference:
Conversion Formula
To find the diameter when you know the circumference, just divide by pi (approximately 3.14).
Example: If a circle has a circumference of 31.4 cm, what is its diameter?
Step 1: Start with the circumference → 31.4 cm
Step 2: Divide by π → 31.4 ÷ 3.14
Step 3: Calculate the result → 10 cm
So a circle with circumference 31.4 cm has a diameter of 10 cm.
Conversion Tip
To find circumference from diameter, use: Circumference = π × Diameter
Real-World Examples
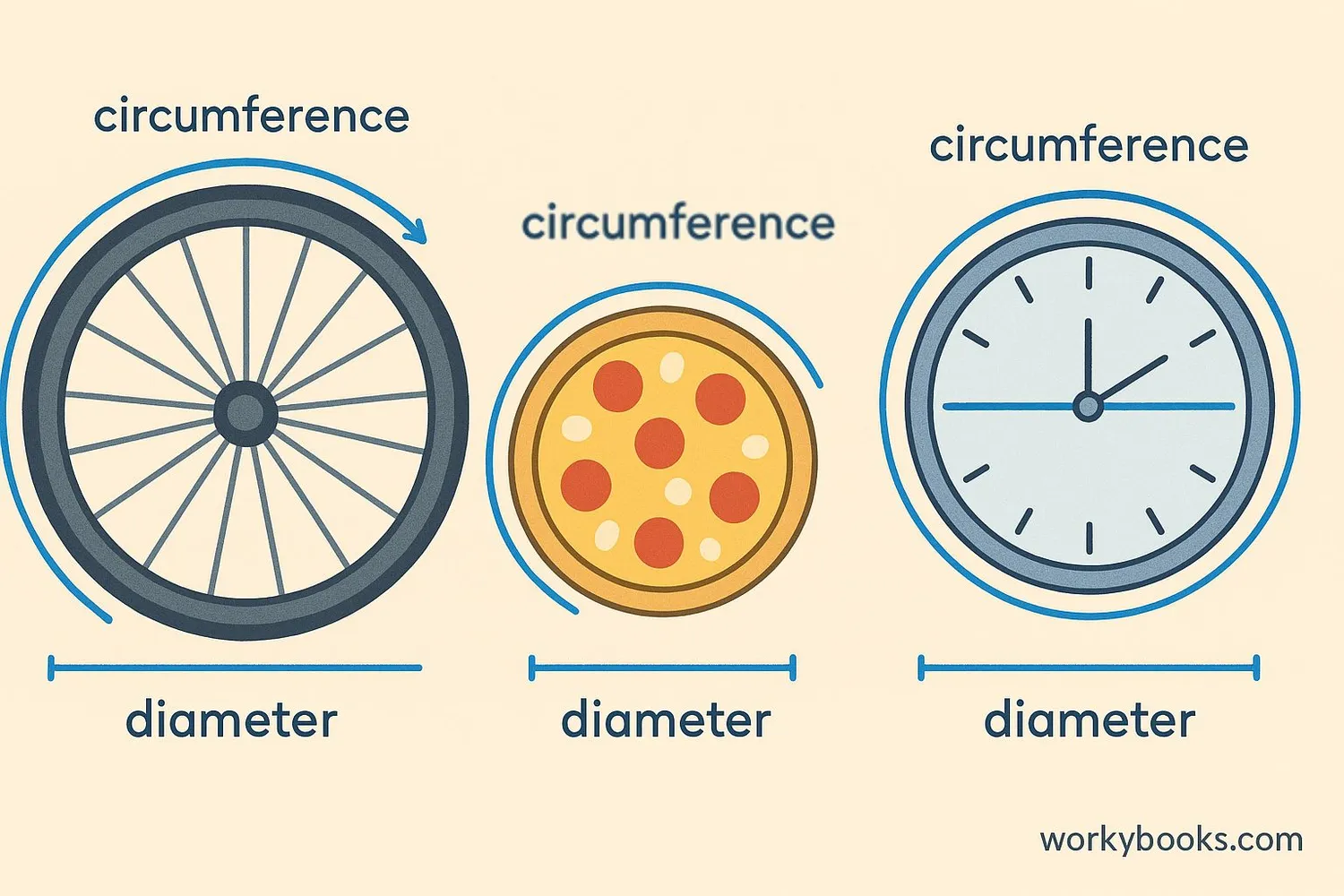
Let's practice with some real-world examples:
Example 1: A bicycle wheel has a circumference of 2.2 meters. What is its diameter?
Solution: Diameter = Circumference ÷ π = 2.2 ÷ 3.14 ≈ 0.7 meters
Example 2: A circular pizza has a circumference of 75 cm. What is its diameter?
Solution: Diameter = 75 ÷ 3.14 ≈ 23.89 cm (about 24 cm)
Example 3: A circular clock has a diameter of 30 cm. What is its circumference?
Solution: Circumference = π × Diameter = 3.14 × 30 = 94.2 cm
Example 4: A hula hoop has a circumference of 3.14 meters. What is its diameter?
Solution: Diameter = 3.14 ÷ 3.14 = 1 meter
Practice finding circular objects around you and measure their circumference to calculate diameter!
Common Conversions
| Circumference | Diameter (using π≈3.14) |
|---|---|
| 31.4 cm | 10 cm |
| 62.8 cm | 20 cm |
| 15.7 cm | 5 cm |
| 47.1 cm | 15 cm |
| 78.5 cm | 25 cm |
| 94.2 cm | 30 cm |
| 125.6 cm | 40 cm |
Pattern Tip
Notice that when circumference is about 3.14 times bigger than diameter? That's π at work!
Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about circles:
Circle Trivia
Discover interesting facts about circles and pi:
Pi Day
March 14 (3/14) is celebrated as Pi Day around the world! Many people enjoy eating pie on this day to celebrate the mathematical constant π (pi).
Endless Digits
Pi is an irrational number, meaning it goes on forever without repeating. Computers have calculated pi to over 50 trillion digits, but we only need a few for most calculations.
Circles in Nature
Circles appear everywhere in nature! Bubbles form spheres (3D circles) because this shape uses the least surface area to contain a given volume. Many flowers grow in circular patterns.
Ancient Circles
Stonehenge, built over 4000 years ago, is arranged in circular patterns. Ancient people understood the importance of circles long before modern mathematics!





