Common Denominators - Definition, Examples, Quiz, FAQ, Trivia
Learn to work with fractions using common denominators with step-by-step guides and practice activities
What is a Common Denominator?

A common denominator is a shared multiple of the denominators of two or more fractions. When fractions have the same denominator, we call them like fractions. This makes it much easier to compare, add, or subtract fractions.
For example, the fractions
12 and
13
have denominators of 2 and 3. A common denominator for these fractions would be 6 because 6 is a multiple of both 2 and 3. We can rewrite both fractions with denominator 6:
12 =
36 and
13 =
26
Key Concept
The Least Common Denominator (LCD) is the smallest common multiple of the denominators. Using the LCD makes fraction operations simpler.
Why Are Common Denominators Important?
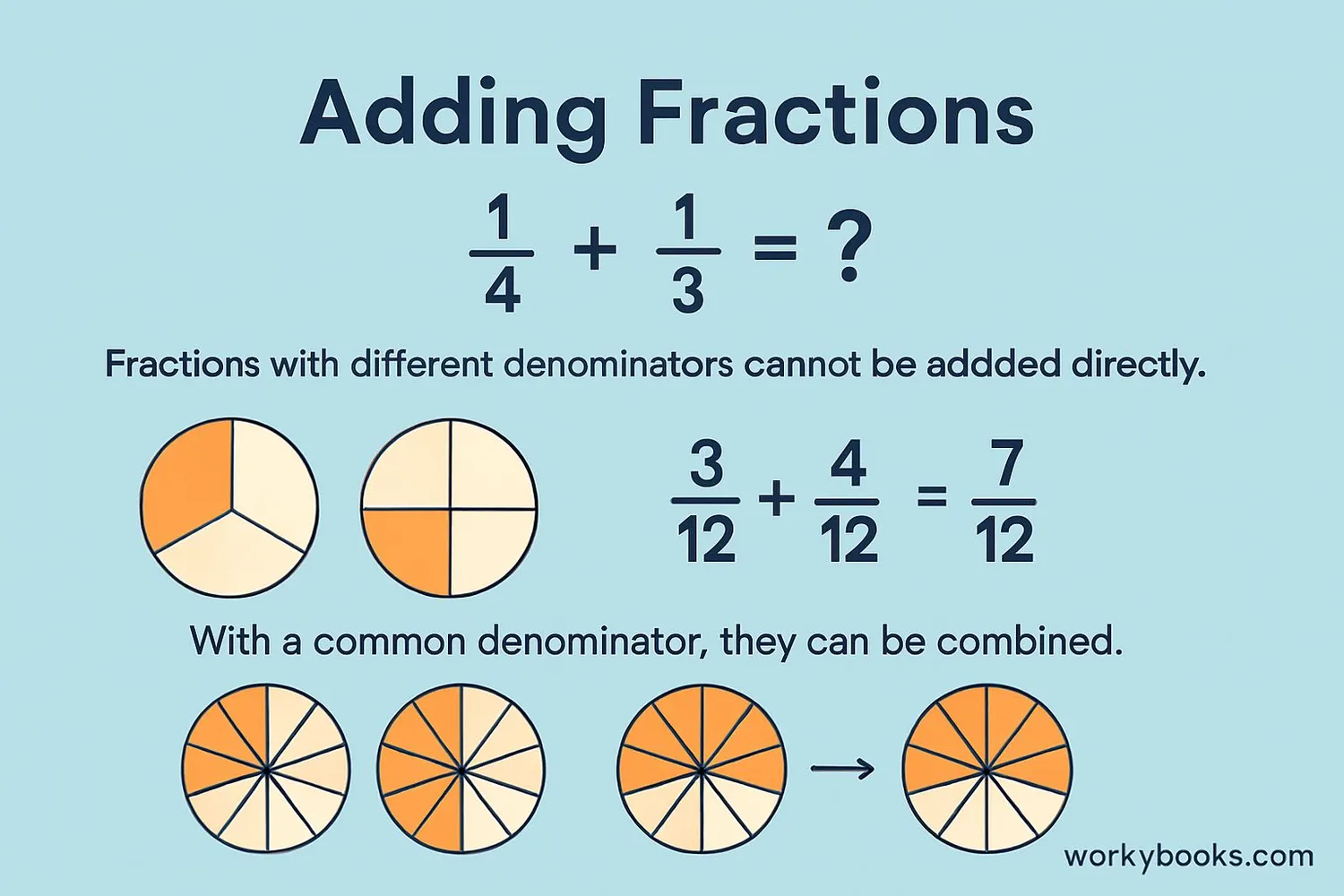
Common denominators are essential for several fraction operations:
Adding and Subtracting Fractions: You can only add or subtract fractions when they have the same denominator. For example, to add
12 +
13,
we first find a common denominator (6), convert to
36 +
26 =
56.
Comparing Fractions: With common denominators, it's easy to see which fraction is larger. For example,
34 vs
23
becomes
912 vs
812,
so we can clearly see 9/12 is larger.
Ordering Fractions: To arrange fractions from smallest to largest, we first give them a common denominator.
Without common denominators, these operations would be very difficult!
How to Find a Common Denominator

There are two main methods for finding common denominators. Let's explore both:
Method 1: Cross-Multiplication
This method works well for two fractions:
- Multiply the numerator and denominator of the first fraction by the denominator of the second fraction
- Multiply the numerator and denominator of the second fraction by the denominator of the first fraction
- Now both fractions have the same denominator (the product of the two original denominators)
Example: For
12 and
13:
Multiply first fraction by 3/3:
1 × 32 × 3 =
36
Multiply second fraction by 2/2:
1 × 23 × 2 =
26
Method 2: Using the LCM (Least Common Multiple)
This method finds the smallest possible common denominator:
- Find the Least Common Multiple (LCM) of the denominators
- Convert each fraction to an equivalent fraction with the LCM as the denominator
- This gives you fractions with the Least Common Denominator (LCD)
Example: For
14 and
16:
LCM of 4 and 6 is 12
Convert first fraction:
1 × 34 × 3 =
312
Convert second fraction:
1 × 26 × 2 =
212
Remember
The LCD method gives the smallest possible denominator, which often makes calculations easier.
Common Denominator Examples

Let's look at some examples of finding and using common denominators:
Example 1: Add
25 +
13
Using cross-multiplication:
Convert to common denominator 15:
2 × 35 × 3 =
615 and
1 × 53 × 5 =
515
Add: 615 +
515 =
1115
Example 2: Compare
38 and
25
Using LCD method:
LCM of 8 and 5 is 40
Convert:
3 × 58 × 5 =
1540 and
2 × 85 × 8 =
1640
Since 15/40 < 16/40, 3/8 < 2/5
Example 3: Subtract
712 -
14
Using LCD: LCM of 12 and 4 is 12
Convert second fraction:
1 × 34 × 3 =
312
Subtract:
712 -
312 =
412 =
13
Practice Tip
Always simplify your fractions after finding a common denominator and performing the operation.
Common Denominator Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about common denominators:
Fraction Trivia
Discover interesting facts about fractions and denominators:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they only used unit fractions (fractions with numerator 1) like 1/2, 1/3, 1/4. They expressed other fractions as sums of unit fractions.
Fraction Origins
The word "fraction" comes from the Latin word "fractus" meaning "broken". This makes sense because fractions represent "broken" numbers or parts of a whole.
Measurement Fractions
In the United States, measurements often use fractions: rulers show inches divided into halves, quarters, eighths, and sixteenths. Carpenters frequently work with fractions when measuring materials.
Decimal Connection
All fractions can be expressed as decimals. For example, 1/2 = 0.5, 1/4 = 0.25, and 1/3 = 0.333... The decimal system is actually based on fractions with denominators that are powers of 10.





