Common Multiples - Definition, Examples, Quiz, FAQ, Trivia
Learn about multiples, common multiples, and how to find the least common multiple with simple explanations and activities
What are Multiples?

A multiple of a number is what you get when you multiply that number by a whole number (1, 2, 3, 4, ...).
Example: The multiples of 4 are:
4 × 1 = 4
4 × 2 = 8
4 × 3 = 12
4 × 4 = 16
4 × 5 = 20
And so on: 24, 28, 32, 36, 40, ...
Think of multiples as "skip counting" by a number. For example, when you skip count by 5s (5, 10, 15, 20, ...), you're listing multiples of 5!
Key Concept
Multiples are the results you get when you multiply a number by whole numbers. They go on forever!
What are Common Multiples?
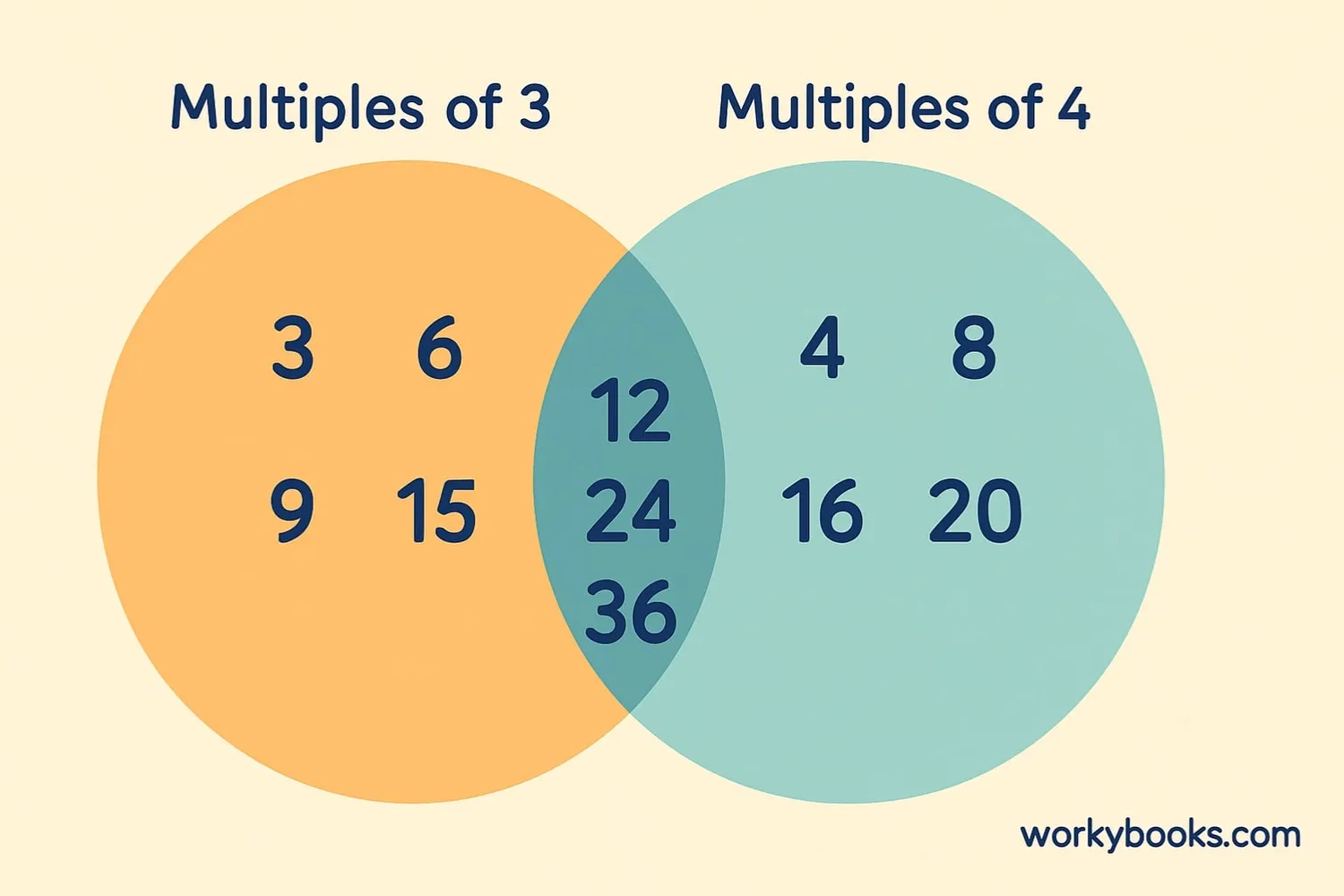
Common multiples are multiples that two or more numbers share. They appear in the multiplication tables of each number.
Example: Let's find common multiples of 3 and 4
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
The common multiples of 3 and 4 are: 12, 24, 36, 48, ...
We can see that 12 appears in both lists, 24 appears in both, and so on.
Remember
Two numbers always have common multiples. The smallest common multiple (other than 0) is called the Least Common Multiple (LCM).
Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of each of them (excluding zero).
Why is LCM important? We use LCM in many real-life situations:
- Scheduling events that repeat at different intervals
- Adding and subtracting fractions with different denominators
- Solving problems where things happen at the same time
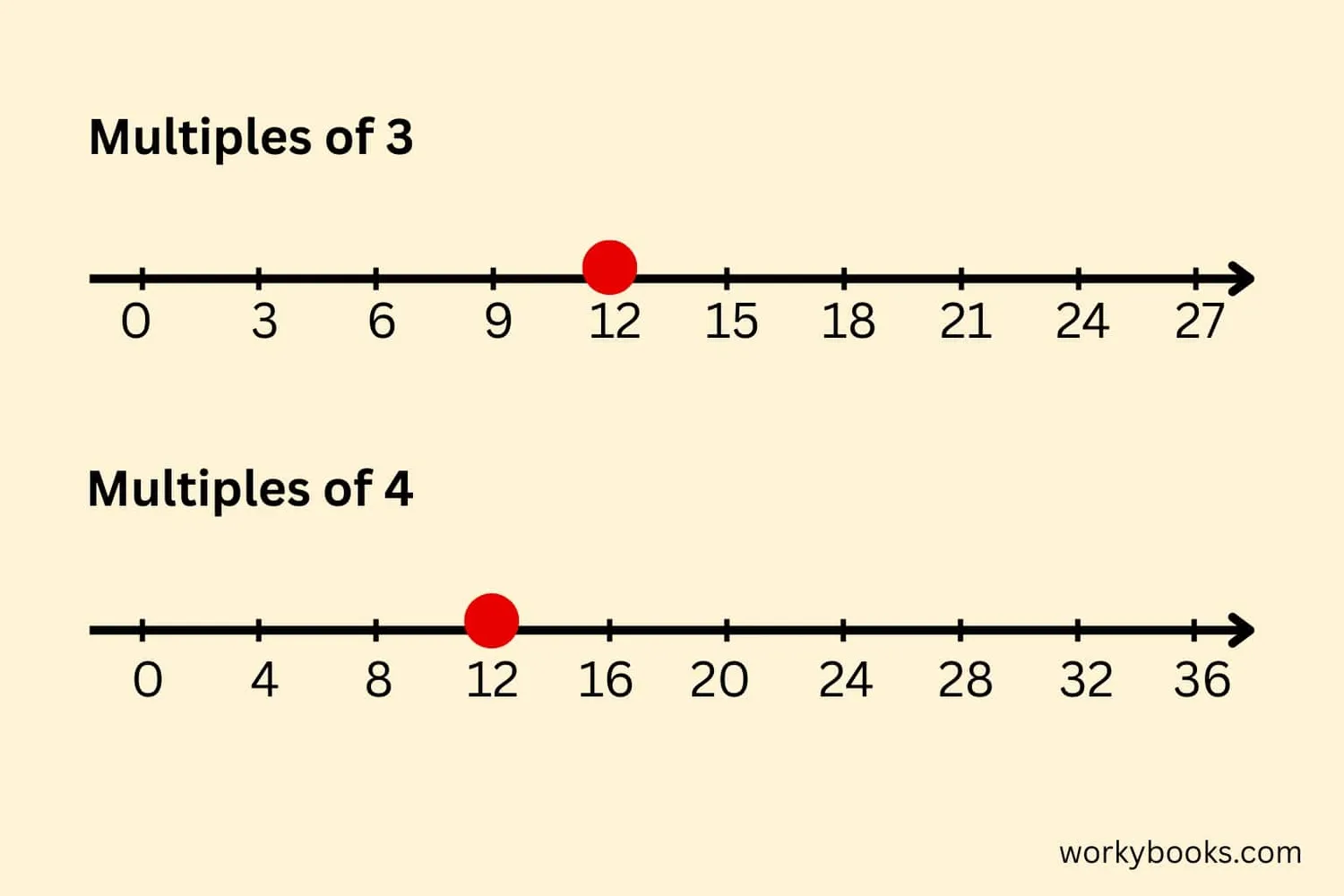
Example: Find the LCM of 3 and 4
Multiples of 3: 3, 6, 9, 12, 15, 18, ...
Multiples of 4: 4, 8, 12, 16, 20, ...
The smallest number that appears in both lists is 12. So LCM(3,4) = 12
Definition
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is divisible by each of them.
Methods to Find LCM

There are several ways to find the LCM of two or more numbers:
Method 1: Listing Multiples
- List several multiples of each number
- Find the smallest multiple that appears in all lists
- This is the LCM
Method 2: Prime Factorization
- Write each number as a product of its prime factors
- For each prime number, take the highest power that appears
- Multiply these together to get the LCM
Example: Find LCM of 12 and 18 using prime factorization
12 = 2 × 2 × 3 = 2² × 3
18 = 2 × 3 × 3 = 2 × 3²
Highest powers: 2² and 3²
LCM = 2² × 3² = 4 × 9 = 36
Method 3: Using GCF
Relationship Between GCF and LCM
For two numbers, the LCM equals their product divided by their Greatest Common Factor
Examples of Common Multiples and LCM

Let's practice with some real-world examples:
Example 1: Find the LCM of 6 and 8
Multiples of 6: 6, 12, 18, 24, 30, 36, ...
Multiples of 8: 8, 16, 24, 32, 40, ...
The smallest common multiple is 24. So LCM(6,8) = 24
Example 2: Find the LCM of 4, 5, and 6
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, ...
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, ...
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
The smallest number that appears in all three lists is 60. So LCM(4,5,6) = 60
Example 3: Real-world problem
Sarah waters her plants every 3 days and Tom waters his plants every 4 days. If they both water their plants today, how many days until they both water on the same day again?
Solution: Find LCM of 3 and 4 → 12 days
Practice Quiz
Test your knowledge about common multiples and LCM with this 5-question quiz:
Frequently Asked Questions
Here are answers to common questions about common multiples:
Math Trivia
Discover interesting facts about multiples and numbers:
Ancient Multiples
The concept of common multiples dates back to ancient Greek mathematicians. Euclid described an algorithm to find the greatest common divisor around 300 BC, which is related to finding LCM.
LCM in Nature
Cicadas use prime number life cycles (13 or 17 years) to minimize overlap with predators. This is nature's way of using LCM concepts to ensure survival!
LCM of Large Numbers
The LCM of all numbers from 1 to 10 is 2,520. For 1 to 20, it's 232,792,560. Calculating these requires finding the highest power of each prime in the range.
Infinite Multiples
Every number has infinitely many multiples. For example, the multiples of 7 go on forever: 7, 14, 21, 28, 35... and so on without end!





