Common Numerators - Definition, Examples, Quiz, FAQ, Trivia
Learn how common numerators help us compare and understand fractions
Understanding Fractions
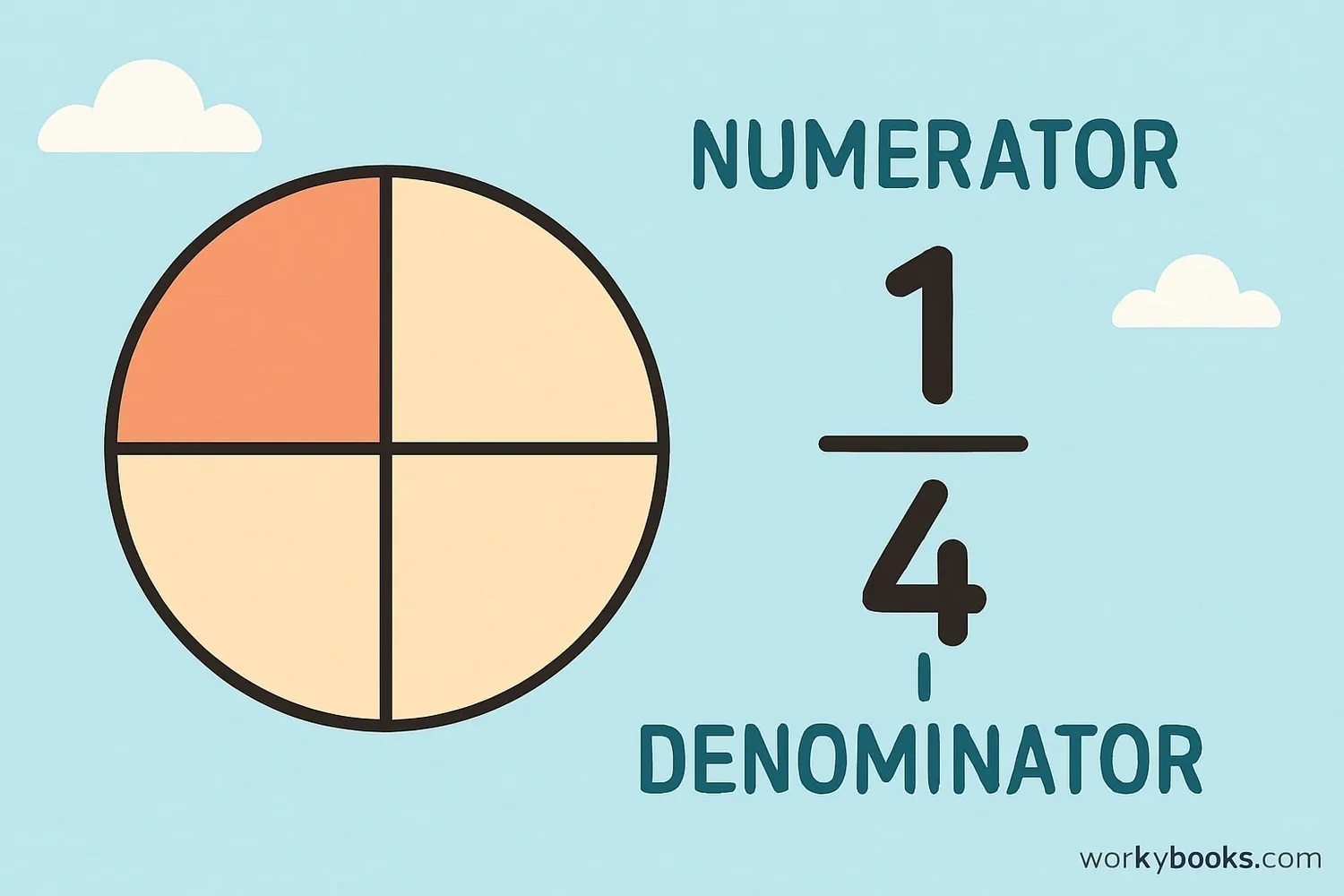
A fraction has two parts:
Numerator: The top number that tells how many parts we have.
Denominator: The bottom number that tells how many equal parts make a whole.
For example, in the fraction ¾:
- Numerator is 3 (we have 3 parts)
- Denominator is 4 (the whole is divided into 4 equal parts)
Fractions help us represent parts of a whole. The numerator and denominator work together to show how much of something we have.
Key Concept
The numerator counts the parts we have, while the denominator tells us how many parts make up the whole.
What is a Common Numerator?
A common numerator means two or more fractions have the same numerator but different denominators.
For example:
⅗ and ⅜ have a common numerator of 3.
When fractions share the same numerator, we can compare them more easily. The fraction with the smaller denominator is actually the larger fraction.
Why? Because when the numerator is the same, the denominator tells us how many pieces the whole is divided into. Smaller denominator means bigger pieces!
Remember
When numerators are the same, the fraction with the smaller denominator is larger because each piece is bigger.
Finding Common Numerators
Sometimes fractions don't start with the same numerator, but we can make them have a common numerator by finding equivalent fractions.
Here's how:
Step 1: Look at the numerators of the fractions you want to compare.
Step 2: Find a number that both numerators can multiply into (like finding a common multiple).
Step 3: Multiply both the numerator and denominator of each fraction to make their numerators the same.
Example: Compare ⅔ and ¾
Multiply 2/3 by 3/3 to get 6/9
Multiply 3/4 by 2/2 to get 6/8
Now we can see that 6/8 > 6/9 because 8 < 9
Remember
When creating equivalent fractions, you must multiply both numerator and denominator by the same number.
Real-World Examples
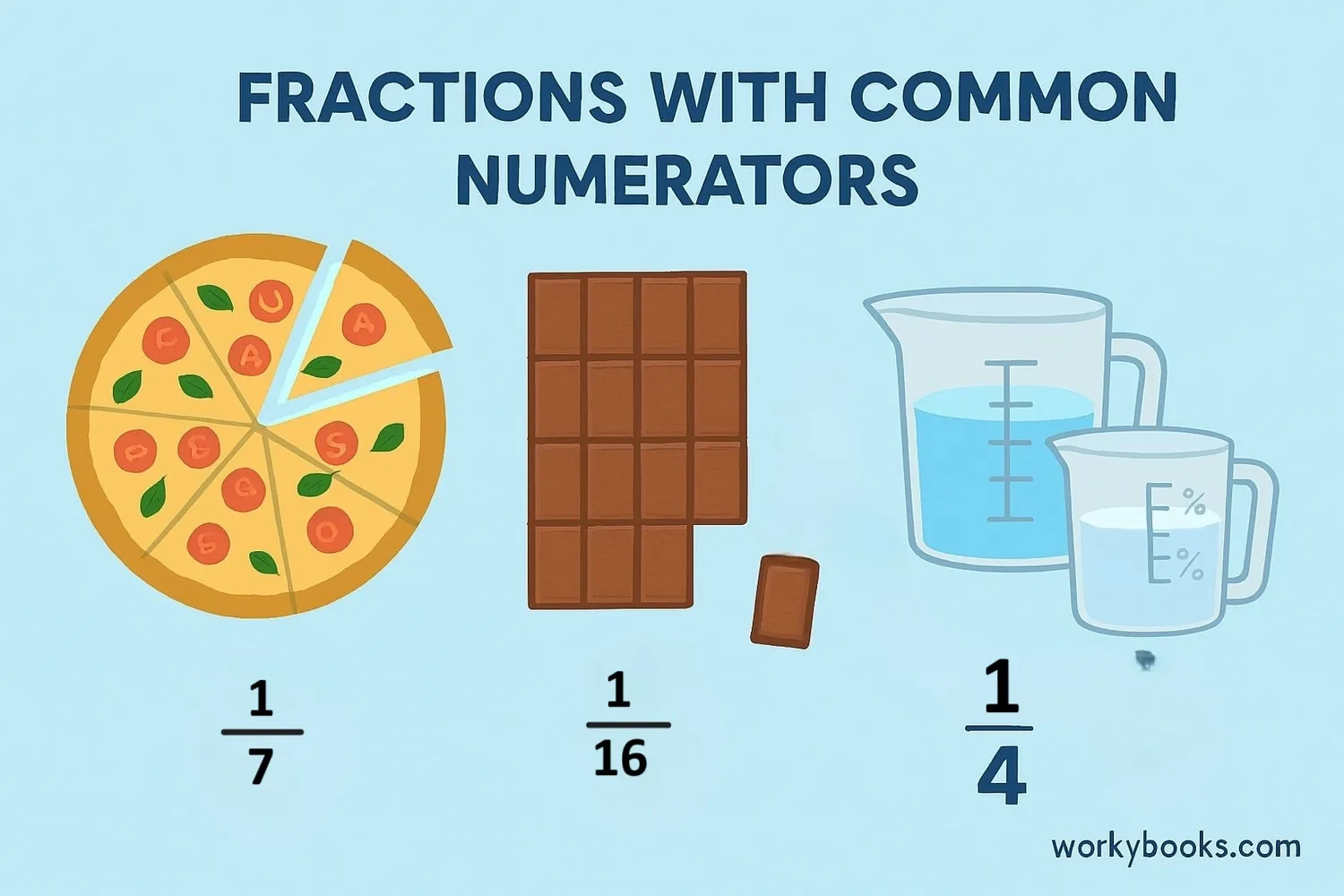
Let's see how common numerators work in real life:
Example 1: Pizza slices
- You have 3 slices of a pizza cut into 8 pieces: ⅜
- Your friend has 3 slices of a pizza cut into 6 pieces: ⅜
- Who has more pizza? Since numerators are the same (3), and 6 < 8, your friend has larger pieces, so they have more pizza!
Example 2: Chocolate bars
- Bar A: You have 2 pieces out of 5 (⅖)
- Bar B: You have 2 pieces out of 3 (⅔)
- Since numerators are the same (2), and 3 < 5, Bar B gives you larger pieces, so you have more chocolate with Bar B!
Example 3: Measuring cups
- Cup A: ¾ full
- Cup B: ⅗ full
- We can make common numerators: ¾ = 15/20, ⅗ = 12/20 → 15/20 > 12/20 so Cup A has more liquid.
Application Tip
Common numerators help us compare things fairly when we have the same number of parts but different sized parts.
Fractions Practice Quiz
Test your understanding of common numerators with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about common numerators:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They had special symbols for fractions with 1 in the numerator, like 1/2, 1/4, and 1/8. These are called unit fractions.
Fraction Origins
The word "fraction" comes from the Latin word "fractio" which means "to break". This makes sense because fractions represent broken pieces of a whole.
Fractions in Nature
Honeybees use fractions in their honeycomb! The hexagonal cells are arranged in a pattern that uses the least amount of wax while storing the most honey - a mathematical optimization using fractions.
Fraction Record
The fraction with the largest denominator ever used in a published mathematical proof has a denominator of 10^10^10^34 (that's 1 followed by 10^34 zeros)!


