Commutative Property of Multiplication - Definition, Examples, Quiz, FAQ, Trivia
Learn how changing the order of numbers doesn't change the product
What is the Commutative Property?

The commutative property of multiplication is a fundamental rule in math that says: changing the order of the factors does not change the product. This means that when you multiply two numbers together, it doesn't matter which number comes first.
For example: 3 × 4 = 12 and 4 × 3 = 12. Both equations give the same result even though the numbers are in different order.
Why is this important? This property makes multiplication flexible and helps us solve problems more easily. It's one of several multiplication properties that help us understand how numbers work together.
Commutative Property Definition
For any numbers a and b, the product remains the same regardless of order.
Key Concept
The commutative property only works for addition and multiplication. It does NOT work for subtraction or division.
How the Commutative Property Works
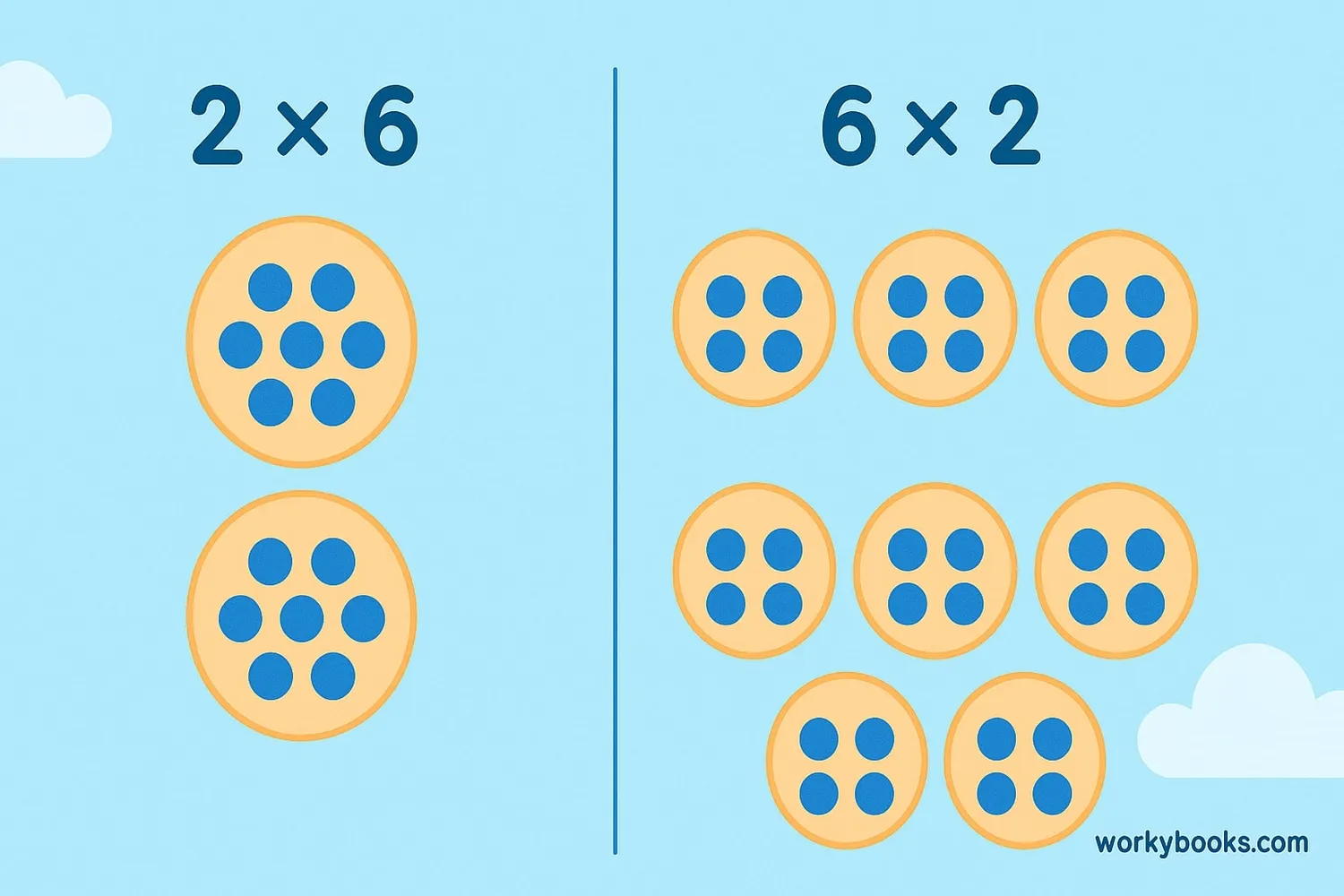
The commutative property works because multiplication is about combining groups of equal size. Whether you have 3 groups of 4 items or 4 groups of 3 items, you still have 12 items total.
Think of it like arranging chairs in a room:
- 4 rows with 6 chairs each: 4 × 6 = 24 chairs
- 6 rows with 4 chairs each: 6 × 4 = 24 chairs
Multiplication Properties Comparison
| Property | Definition | Example |
|---|---|---|
| Commutative | Order doesn't change product | 4 × 3 = 3 × 4 |
| Associative | Grouping doesn't change product | (2 × 3) × 4 = 2 × (3 × 4) |
| Distributive | Multiplying a sum by a number | 3 × (4 + 5) = (3 × 4) + (3 × 5) |
| Identity | Multiplying by 1 gives same number | 7 × 1 = 7 |
| Zero | Multiplying by 0 gives 0 | 9 × 0 = 0 |
Remember
The commutative property only applies to addition and multiplication. It does NOT work for subtraction or division.
Examples of Commutative Property
Numbers
Both give the same product
Larger Numbers
Product remains the same
Variables
True for any values of m and n
Real-World Examples:
Example 1: Sarah has 4 bags with 5 apples each. Michael has 5 bags with 4 apples each. Who has more apples?
Solution: Both have the same: 4 × 5 = 20 and 5 × 4 = 20 apples.
Example 2: A classroom has 6 rows with 7 desks each. If rearranged to 7 rows, how many desks per row?
Solution: 6 × 7 = 42 desks total. 42 ÷ 7 = 6 desks per row.
Example 3: Calculate 25 × 4 and 4 × 25. What do you notice?
Solution: Both equal 100. The commutative property holds true.
Practice Tip
When solving multiplication problems, you can choose the order that makes calculation easier. For example, 5 × 16 might be easier than 16 × 5.
Practice Quiz
Test your understanding with these 5 questions about the commutative property:
Frequently Asked Questions
Common questions about the commutative property:
Math Trivia
Discover interesting facts about multiplication and math properties:
Ancient Multiplication
The commutative property was recognized by ancient mathematicians. Egyptian and Babylonian mathematicians used this property in their calculations over 4,000 years ago.
Math in Nature
The commutative property applies to many natural phenomena. For example, when calculating the total number of spots on ladybugs in two groups, the order doesn't matter.
Math in Space
Astronomers use commutative property when calculating distances. Multiplying the number of light-years by the number of stars in a galaxy gives the same result in any order.
Large Number Multiplication
The commutative property holds true even for enormous numbers. For example, 123,456 × 789,012 = 789,012 × 123,456, though both are challenging calculations!





