Comparing Decimals - Definition, Examples, Quiz, FAQ, Trivia
Learn to compare and order decimal numbers with easy explanations and practice activities
What is Comparing Decimals?
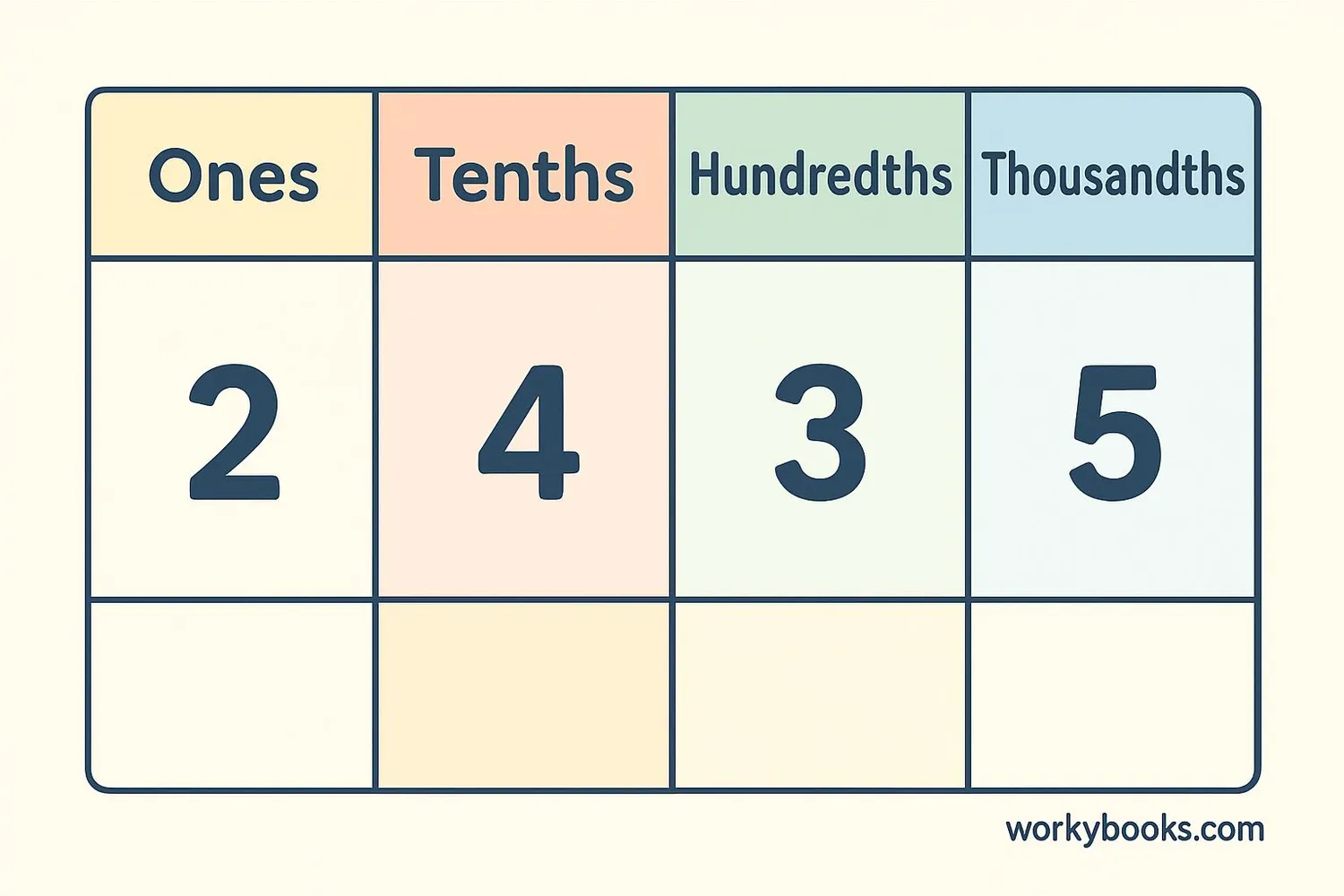
Comparing decimals means determining which decimal number is larger or smaller. Decimals are numbers that have a whole number part and a fractional part separated by a decimal point. For example, 3.25 and 4.1 are decimals.
Why do we need to compare decimals? We use decimal comparisons in many real-life situations like comparing prices at the store, measuring ingredients for recipes, or understanding sports statistics. Being able to compare decimals helps us make good decisions and understand the world around us.
To compare decimals, we look at the digits in each place value from left to right. The decimal place values after the decimal point are:
Key Concept
When comparing decimals, start by looking at the digits to the left of the decimal point (the whole numbers). If they are different, the larger whole number means the decimal is larger. If they are the same, then compare the digits to the right of the decimal point, one place at a time.
How to Compare Decimals
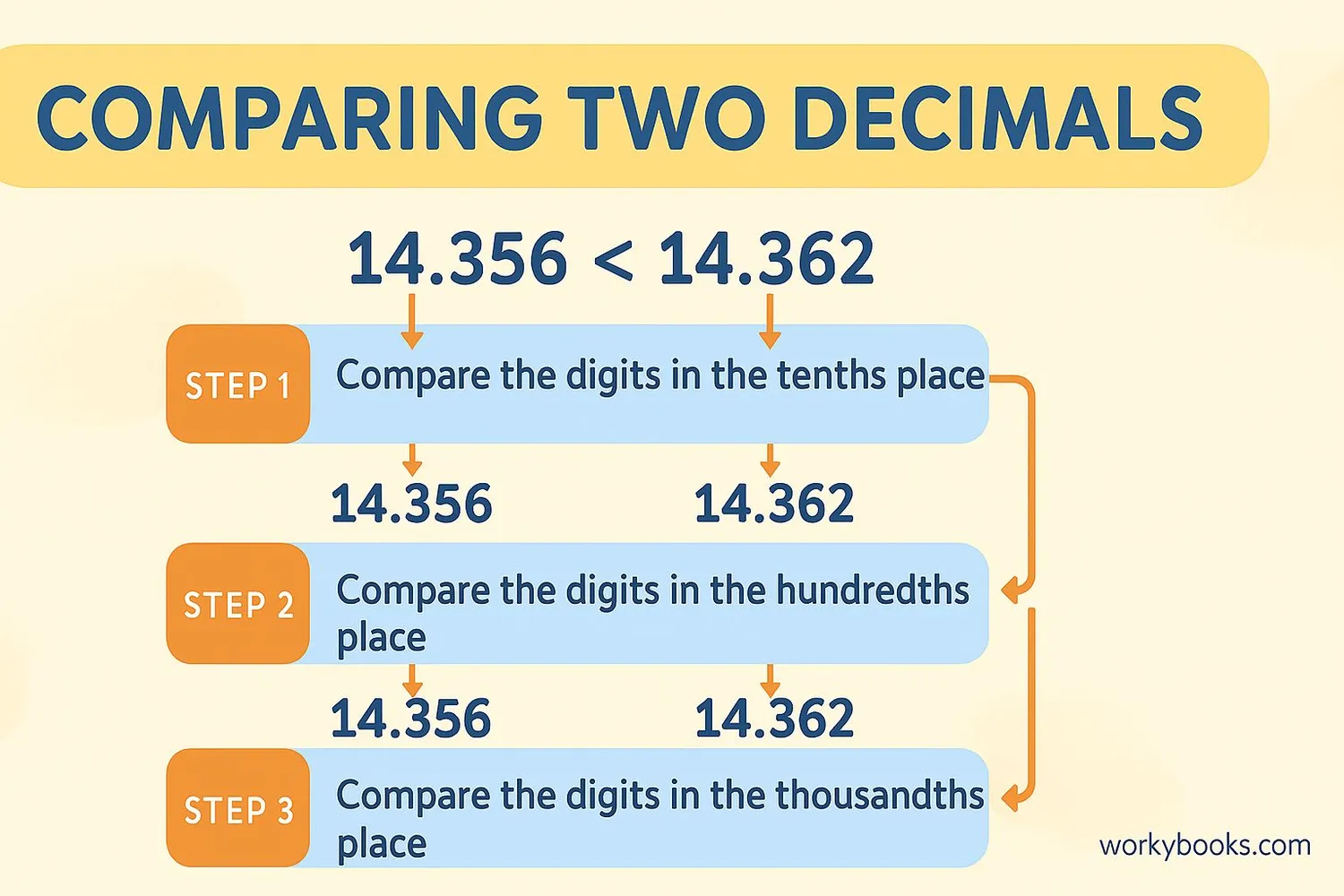
Follow these steps to compare any two decimal numbers:
Step 1: Compare the whole number parts (the digits to the left of the decimal point).
Example: 15.7 and 8.95 → 15 is greater than 8, so 15.7 > 8.95
Step 2: If the whole numbers are the same, compare the tenths place (first digit after the decimal).
Example: 6.3 and 6.25 → Whole numbers are equal (6=6), tenths: 3 > 2, so 6.3 > 6.25
Step 3: If the tenths are the same, compare the hundredths place (second digit after decimal).
Example: 4.71 and 4.73 → Whole and tenths equal (4=4, 7=7), hundredths: 1 < 3, so 4.71 < 4.73
Step 4: Continue comparing each decimal place until you find a difference.
Example: 9.405 and 9.402 → All places same until thousandths: 5 > 2, so 9.405 > 9.402
Step 5: If one decimal has fewer digits, you can add zeros to make them the same length.
Example: Compare 7.5 and 7.50 → They are equal (7.50 = 7.5)
Remember
Decimal places determine the value. The tenths place is ten times bigger than the hundredths place. Always compare digits in the same place value position.
Comparing Decimals Examples
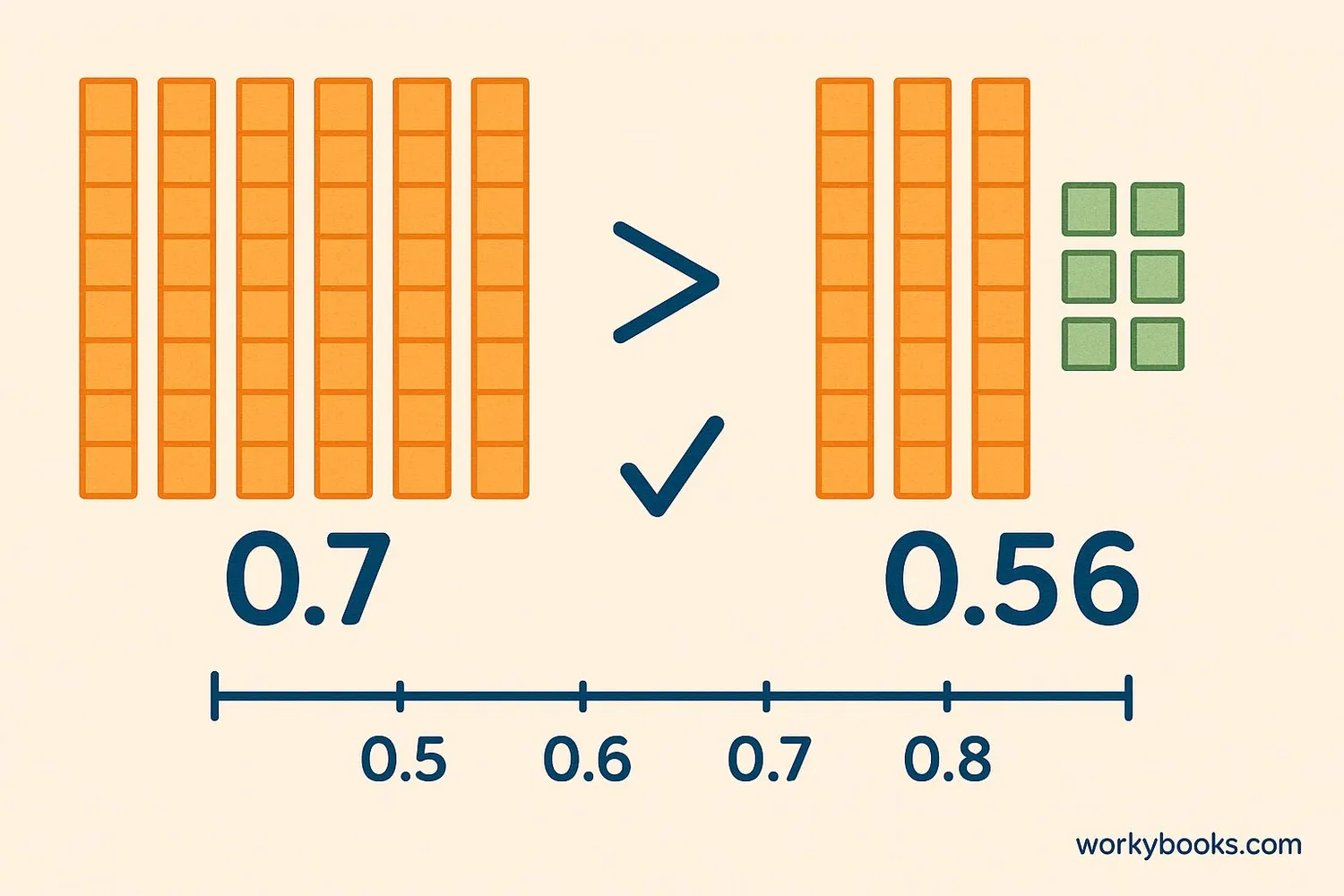
Let's practice comparing decimals with some examples:
Example 1: Which is larger, 0.7 or 0.56?
Solution: Compare the tenths place: 0.7 has 7 tenths, 0.56 has 5 tenths. Since 7 > 5, 0.7 > 0.56.
Example 2: Arrange 1.23, 1.3, 1.19 in order from smallest to largest
Solution:
Step 1: Compare whole numbers - all are 1
Step 2: Compare tenths: 1.23 (2 tenths), 1.3 (3 tenths), 1.19 (1 tenth)
Step 3: Since 1 < 2 < 3, the order is 1.19, 1.23, 1.3
Common Decimal Comparisons
| Decimal Pair | Comparison | Why? |
|---|---|---|
| 0.4 and 0.40 | Equal | Trailing zeros don't change value |
| 3.25 and 3.3 | 3.3 > 3.25 | Tenths: 3 > 2 |
| 0.99 and 1.0 | 1.0 > 0.99 | Whole numbers: 1 > 0 |
| 5.067 and 5.07 | 5.07 > 5.067 | Hundredths: 7 > 6 |
| 2.50 and 2.5 | Equal | Same value |
Practice Tip
When comparing decimals with different digits, add zeros to make them the same length. For example: 0.8 becomes 0.80 when comparing to 0.75.
Decimal Comparison Quiz
Test your decimal comparison skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about comparing decimals:
Decimal Trivia
Discover interesting facts about decimals and their history:
The Decimal Point
The decimal point was first used by Christopher Clavius in 1593. However, the modern decimal system was popularized by Simon Stevin in the 16th century, who called it "decimal fractions".
Precision in Science
Scientists use decimals to express very precise measurements. For example, the mass of an electron is approximately 0.000000000000000000000000000910938356 grams - that's 30 decimal places!
Space Calculations
NASA uses decimals with up to 15 decimal places for precise spacecraft navigation. A tiny decimal error could send a spacecraft millions of miles off course!
Pi Calculation
The world record for calculating the most decimal digits of π is 100 trillion digits! It took a supercomputer 157 days to calculate this in 2022.


