Comparing Ratios - Definition, Examples, Quiz, FAQ, Trivia
Learn how to compare ratios with visual examples and step-by-step methods
What is a Ratio?
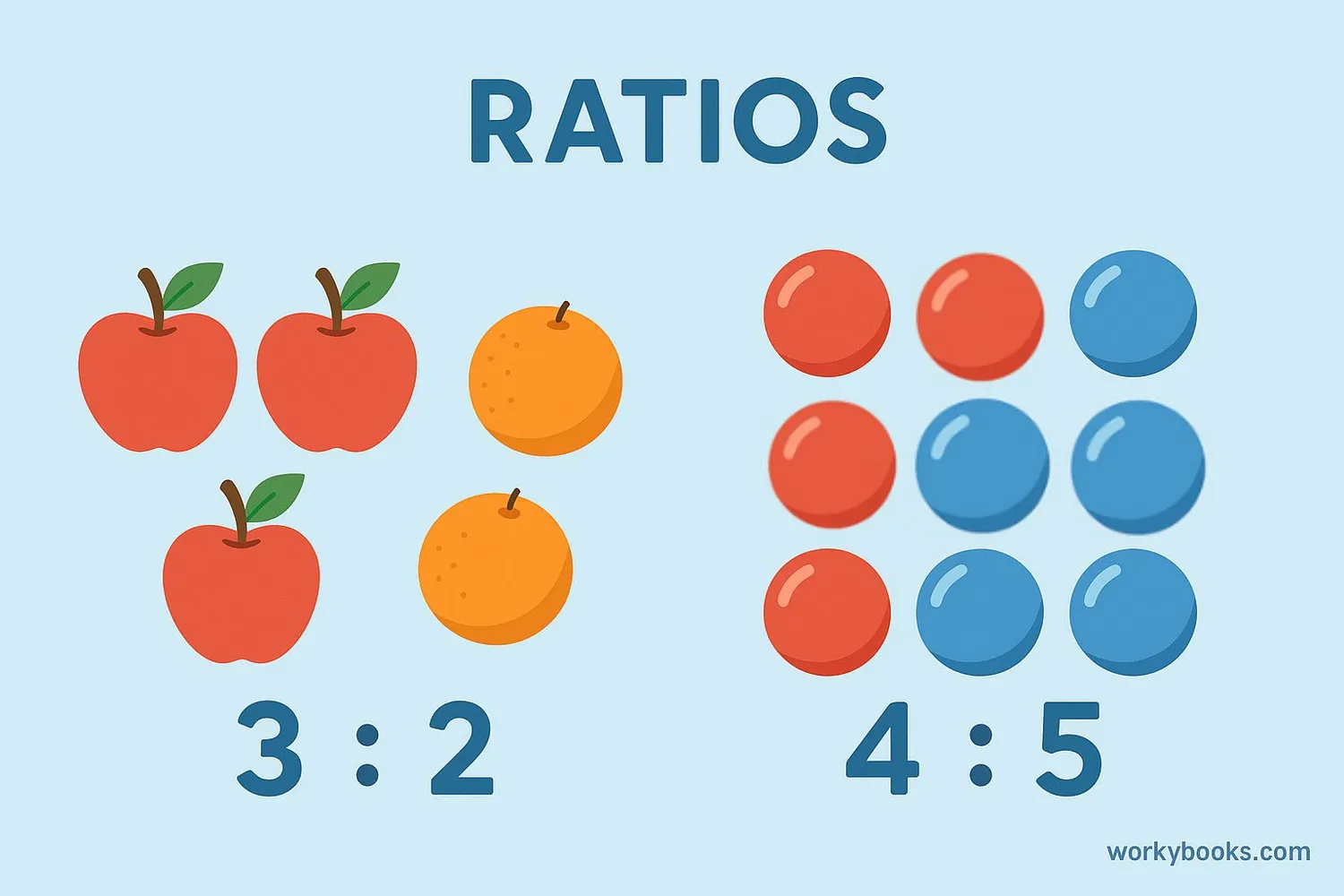
A ratio is a way to compare two or more quantities. It shows how much of one thing there is compared to another thing. Ratios can be written in three different ways:
1. Using "to": 3 to 2
2. As a fraction: 3/2
3. With a colon: 3:2
All three of these mean the same thing! They tell us that for every 3 of the first thing, there are 2 of the second thing.
Key Concept
Ratios help us understand proportional relationships between different quantities.
Equivalent Ratios
Equivalent ratios are different ratios that represent the same relationship. For example, 2:3 is equivalent to 4:6 and 6:9. We can make equivalent ratios by multiplying or dividing both parts of the ratio by the same number.
Comparing Ratios
Comparing ratios helps us understand which relationship is stronger, larger, or more concentrated. We might compare ratios to find:
• Which class has more girls per boy?
• Which juice mixture is more concentrated?
• Which team has a better win-loss record?
To compare ratios accurately, we need to make them equivalent or convert them to decimals or percentages.
Ratio Comparison Formula
To compare two ratios, convert them to decimals by dividing the first number by the second number.
Methods for Comparing Ratios
1. Making Denominators Equal
This method works well when comparing ratios written as fractions. We make the denominators the same and then compare the numerators.
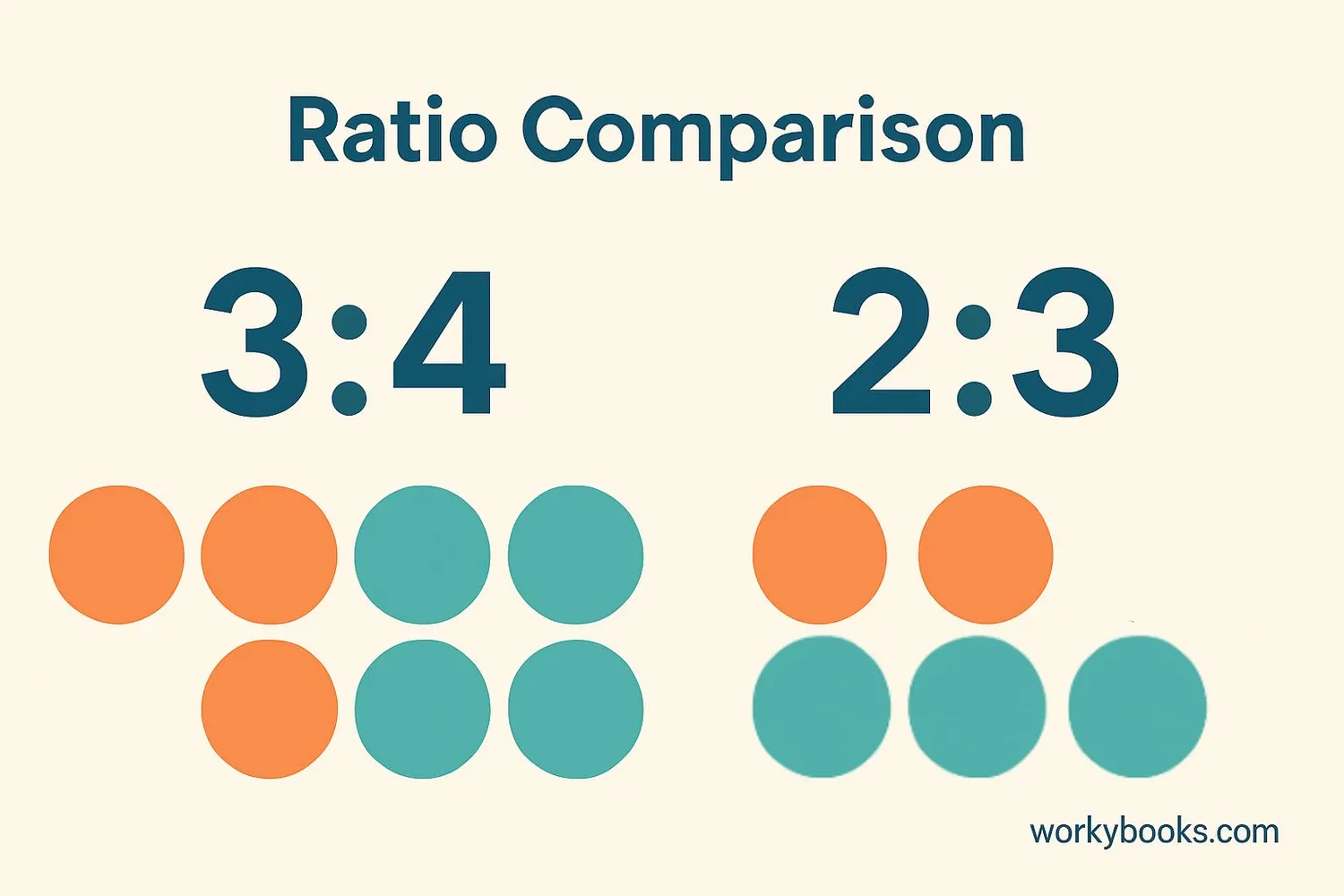
Example: Compare 3:4 and 5:7
Step 1: Write as fractions → 3/4 and 5/7
Step 2: Find common denominator (4×7=28)
Step 3: Convert fractions → (3×7)/28 = 21/28 and (5×4)/28 = 20/28
Step 4: Compare → 21/28 > 20/28 so 3:4 > 5:7
2. Cross Multiplication
This method involves multiplying the numerator of the first ratio with the denominator of the second ratio and vice versa.
Example: Compare 2:5 and 3:7
Step 1: Write as fractions → 2/5 and 3/7
Step 2: Cross multiply → (2×7) = 14 and (3×5) = 15
Step 3: Compare products → 14 < 15 so 2/5 < 3/7
3. Decimal Conversion
Convert each ratio to a decimal by dividing the numerator by the denominator, then compare the decimals.
Example: Compare 4:9 and 3:7
Step 1: Calculate decimals → 4÷9 ≈ 0.444 and 3÷7 ≈ 0.428
Step 2: Compare → 0.444 > 0.428 so 4:9 > 3:7
Solved Examples

Example 1: Classroom Ratios
Class A has 12 girls and 15 boys. Class B has 10 girls and 12 boys. Which class has a higher girl-to-boy ratio?
Solution:
Class A: 12:15 = 4:5 = 0.8
Class B: 10:12 = 5:6 ≈ 0.833
Since 0.833 > 0.8, Class B has a higher girl-to-boy ratio.
Example 2: Recipe Comparison
Recipe A uses 3 cups flour to 2 cups sugar. Recipe B uses 5 cups flour to 3 cups sugar. Which recipe uses more sugar per cup of flour?
Solution:
Compare sugar-to-flour ratios:
Recipe A: 2:3 ≈ 0.667
Recipe B: 3:5 = 0.6
Since 0.667 > 0.6, Recipe A uses more sugar per cup of flour.
Example 3: Sports Win Ratios
Team A won 15 out of 20 games. Team B won 12 out of 15 games. Which team has a better win ratio?
Solution:
Team A: 15:20 = 3:4 = 0.75
Team B: 12:15 = 4:5 = 0.8
Since 0.8 > 0.75, Team B has a better win ratio.
Ratio Comparison Quiz
Test your understanding with these practice questions. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about ratios and ratio comparison:
Math Trivia
Discover interesting facts about ratios and proportions:
Golden Ratio
The Golden Ratio (approximately 1.618) appears throughout nature and art. It's found in seashells, flower petals, famous paintings like the Mona Lisa, and even in the proportions of the human body!
Scale Models
Architects and engineers use ratios to create scale models. A 1:100 scale model means 1 cm on the model represents 100 cm (1 meter) in real life. This helps visualize buildings, bridges, and products before construction.
Space Exploration
NASA scientists use ratios to calculate rocket fuel mixtures, determine planetary distances, and design spacecraft. The ratio of fuel to oxygen must be precise for rockets to reach space successfully.
Extreme Ratios
The largest known prime number has over 24 million digits! If written out, the ratio of its length to a standard book page would be about 8,000 pages of just digits!





