Compensation - Definition, Examples, Quiz, FAQ, Trivia
Learn to solve problems mentally by adjusting numbers and compensating
What is Compensation?

Compensation is a mental math strategy where you adjust one number to make a problem easier to solve, and then compensate for that adjustment later. It's like borrowing a little from one number and giving it to another to create friendlier numbers that are easier to work with.
Think of compensation as a balancing act. When you change one number to make the math simpler, you need to make an opposite change to another number to keep the total the same. This strategy helps you solve problems quickly in your head without needing paper or pencil.
Compensation is especially useful for addition and subtraction problems. It helps you work with numbers that are easier to handle mentally, like multiples of 10 or 5.
Key Concept
Compensation means adjusting numbers to make calculations easier, then compensating for that adjustment to get the correct result.
How to Use the Compensation Strategy

Using the compensation strategy involves just a few simple steps:
Compensation Steps
Change a number to make the problem easier, solve the new problem, then adjust your answer
Example: Solve 38 + 15 using compensation
Step 1: Adjust 38 to 40 by adding 2 (because 40 is easier to work with)
Step 2: Solve the easier problem: 40 + 15 = 55
Step 3: Compensate: Since we added 2 extra to 38, we need to subtract 2 from the answer
Step 4: Correct answer: 55 - 2 = 53
So 38 + 15 = 53. The compensation helped us work with the easier number 40!
Remember
Whatever you do to one number, you must do the opposite to the other number or to the result to keep the balance.
Types of Compensation
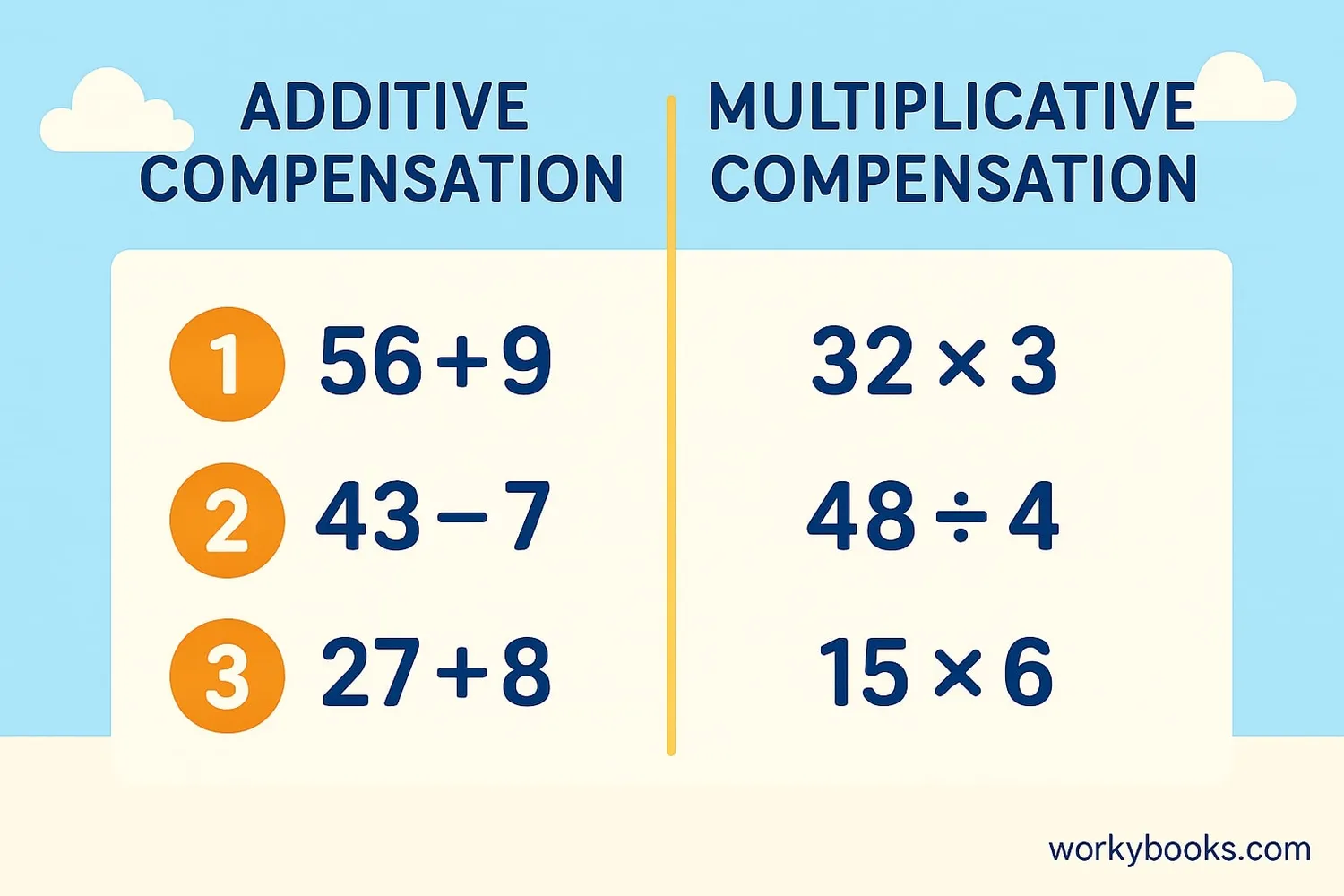
There are two main types of compensation that you can use depending on the problem:
Additive Compensation
This type is used for addition and subtraction problems. You adjust numbers by adding or subtracting small amounts to create easier numbers to work with.
Multiplicative Compensation
This type is used for multiplication and division problems. You adjust numbers by multiplying or dividing to create easier numbers.
Strategy Tip
Additive compensation is more common for elementary students, while multiplicative compensation is introduced in later grades.
Practice with Compensation
Let's practice with some examples. Try solving these using the compensation strategy before looking at the solutions:
Example 1: Solve 56 + 19 using compensation
Solution: Add 1 to 19 to make 20 → 56 + 20 = 76 → Subtract 1 → 75
Example 2: Solve 83 - 29 using compensation
Solution: Add 1 to both numbers → 84 - 30 = 54
Example 3: Solve 7 × 16 using compensation
Solution: Halve 16 and double 7 → 14 × 8 = 112
Example 4: Solve 98 + 76 using compensation
Solution: Add 2 to 98 to make 100 → 100 + 76 = 176 → Subtract 2 → 174
Remember: The key is to make one of the numbers easier to work with, usually a multiple of 10 or 5.
Practice Tip
When subtracting, you can add the same amount to both numbers to make subtraction easier without changing the difference.
Compensation Strategy Quiz
Test your understanding of the compensation strategy with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the compensation strategy:
Math Strategy Trivia
Discover interesting facts about math strategies:
Ancient Mental Math
Ancient civilizations like the Egyptians and Babylonians used mental math strategies similar to compensation over 4,000 years ago. They developed these techniques for trade and construction without paper or calculators.
Brain Benefits
Using mental math strategies like compensation strengthens neural pathways in your brain. Studies show that people who regularly practice mental math have better working memory and problem-solving skills.
Calculator vs. Brain
Research shows that solving math problems mentally using strategies like compensation activates more areas of your brain than using a calculator. Mental math exercises help build number sense and mathematical intuition.
Global Math Strategies
Different cultures have developed unique mental math strategies. In Japan, the soroban (abacus) method teaches visualization techniques. In India, Vedic math includes strategies similar to compensation for quick calculations.





