Complementary Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn about angles that add up to 90 degrees with visual examples, practice activities, and real-world connections
What are Complementary Angles?
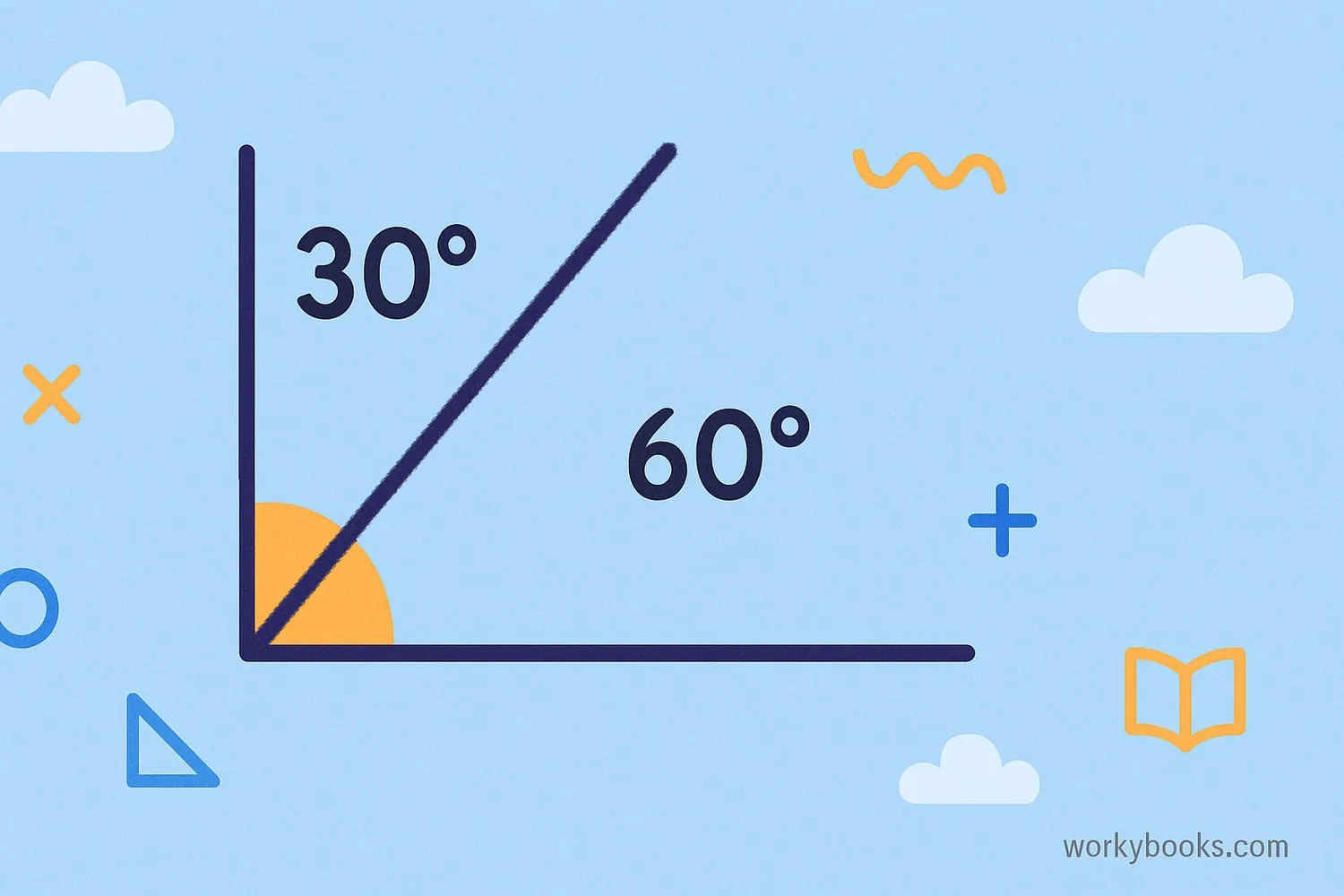
Complementary angles are two angles that add up to 90 degrees. When you put them together, they form a right angle (like the corner of a square).
Think of complementary angles as best friends who complete each other to make a perfect corner. Each angle is the complement of the other.
For example:
- 30° + 60° = 90°
- 45° + 45° = 90°
- 20° + 70° = 90°
These pairs are complementary because together they make 90 degrees. The angles themselves are always acute angles (less than 90°).
Key Concept
Two angles are complementary if the sum of their measures is exactly 90 degrees.
Types of Complementary Angles
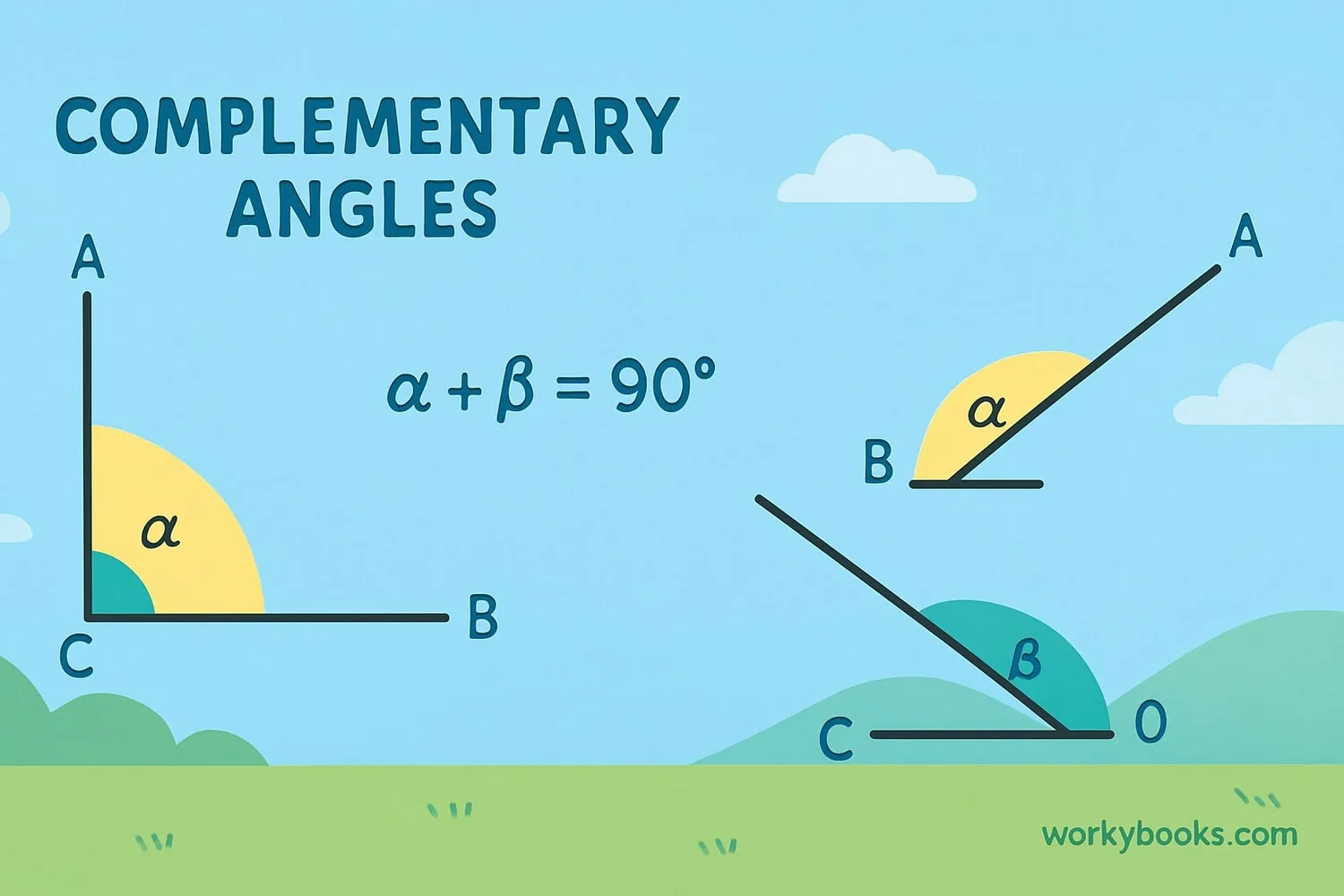
Complementary angles can be either adjacent or non-adjacent:
Adjacent Complementary Angles
These angles share a common vertex and a common side. Together, they form a right angle.
Non-Adjacent Complementary Angles
These angles don't share a common vertex or side, but they still add up to 90 degrees.
Remember
Complementary angles can be anywhere as long as their sum is 90°. They don't need to be next to each other!
Finding Complementary Angles

Finding the complementary angle is easy! Just follow this simple formula:
Complementary Angle Formula
To find the complement of any angle, subtract it from 90 degrees.
Example: What is the complement of a 35° angle?
Step 1: Start with the angle → 35°
Step 2: Subtract from 90° → 90° - 35°
Step 3: Calculate the result → 55°
So the complement of 35° is 55°. They add up to 90°!
Tip
If you know two angles are complementary and one is missing, subtract the known angle from 90° to find the missing angle.
Complementary Angles Theorem
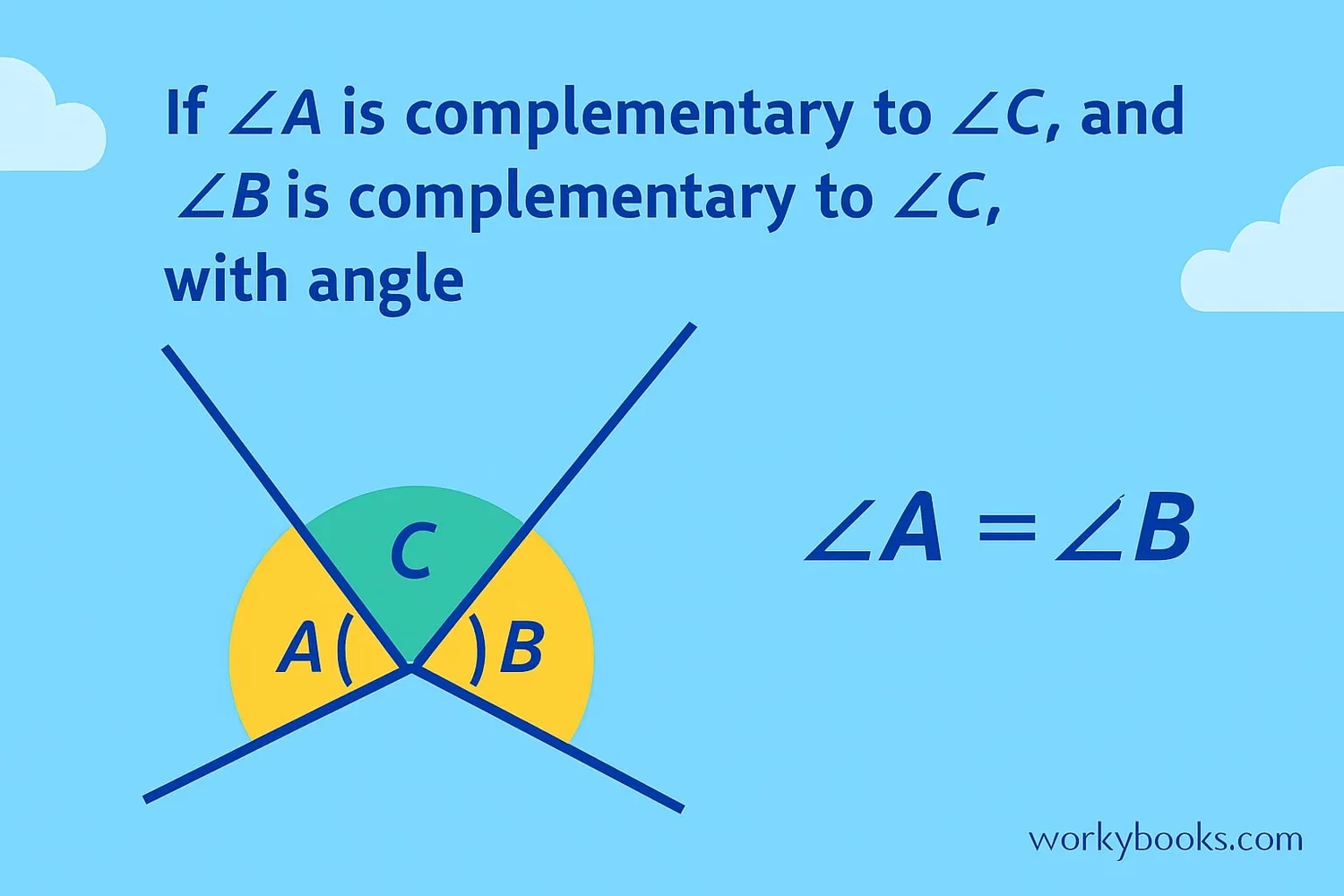
The Complementary Angles Theorem states:
Complementary Angles Theorem
If two angles are complementary to the same angle, then they are congruent to each other.
Example:
- If ∠A + ∠C = 90°
- And ∠B + ∠C = 90°
- Then ∠A = ∠B
Why? Because both ∠A and ∠B complete ∠C to make 90°, so they must be the same size!
Examples and Practice

Let's practice with some real-world examples:
Example 1: A ladder leans against a wall, forming a 65° angle with the ground. What angle does it form with the wall?
Solution: The angles are complementary → 90° - 65° = 25°
Example 2: When a book is opened, the two pages form complementary angles. If one page is at 40°, what's the other?
Solution: 90° - 40° = 50°
Example 3: At 3:00 on a clock, the hour and minute hands form a 90° angle. If you draw a line splitting this angle into two complementary parts, what are the possible angle pairs?
Solution: Any pairs that add to 90°: (30°, 60°), (45°, 45°), (20°, 70°), etc.
Practice: If angle X is 15°, what is its complement?
Answer: 90° - 15° = 75°
Real-World Connection
Complementary angles are everywhere! Look for them in corners of rooms, books, clocks, and even in sports like basketball when players shoot at the basket.
Practice Quiz
Test your knowledge with these 5 questions about complementary angles:
Frequently Asked Questions
Here are answers to common questions about complementary angles:
Angle Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Knowledge
The concept of angles dates back to ancient Babylonian astronomers around 2000 BCE. They used angles to track stars and planets, creating the first known trigonometry tables.
Right Angles in Nature
Honeybees build their hives with perfect hexagonal cells that contain 120° angles. When two hexagons meet, they form 120° angles which are supplementary, not complementary.
Angles in Space Travel
NASA engineers use complementary angle principles when calculating spacecraft trajectories. Small complementary angle adjustments can make huge differences in orbital paths.
The Right Angle Advantage
Buildings and bridges use right angles because they provide the strongest structural support. Complementary angles help engineers calculate stress points in these structures.





