Concurrent Lines - Definition, Examples, Quiz, FAQ, Trivia
Learn about intersecting lines that meet at a common point with visual examples and practice activities
What are Concurrent Lines?
Concurrent Lines Definition
Concurrent lines are three or more straight lines that all pass through the same point.
In geometry, when three or more lines meet at a single point, we call them concurrent lines.
Think of it like a group of friends meeting at the same spot in the playground. Each line is like a path, and they all come together at one special place.
Important facts about concurrent lines:
- They must be straight lines (not curved)
- They must all pass through exactly one common point
- At least three lines are needed to be concurrent
- Concurrent lines are always coplanar (in the same flat surface)
Key Concept
Concurrent lines always meet at a single point, no matter how many lines there are.
Point of Concurrency
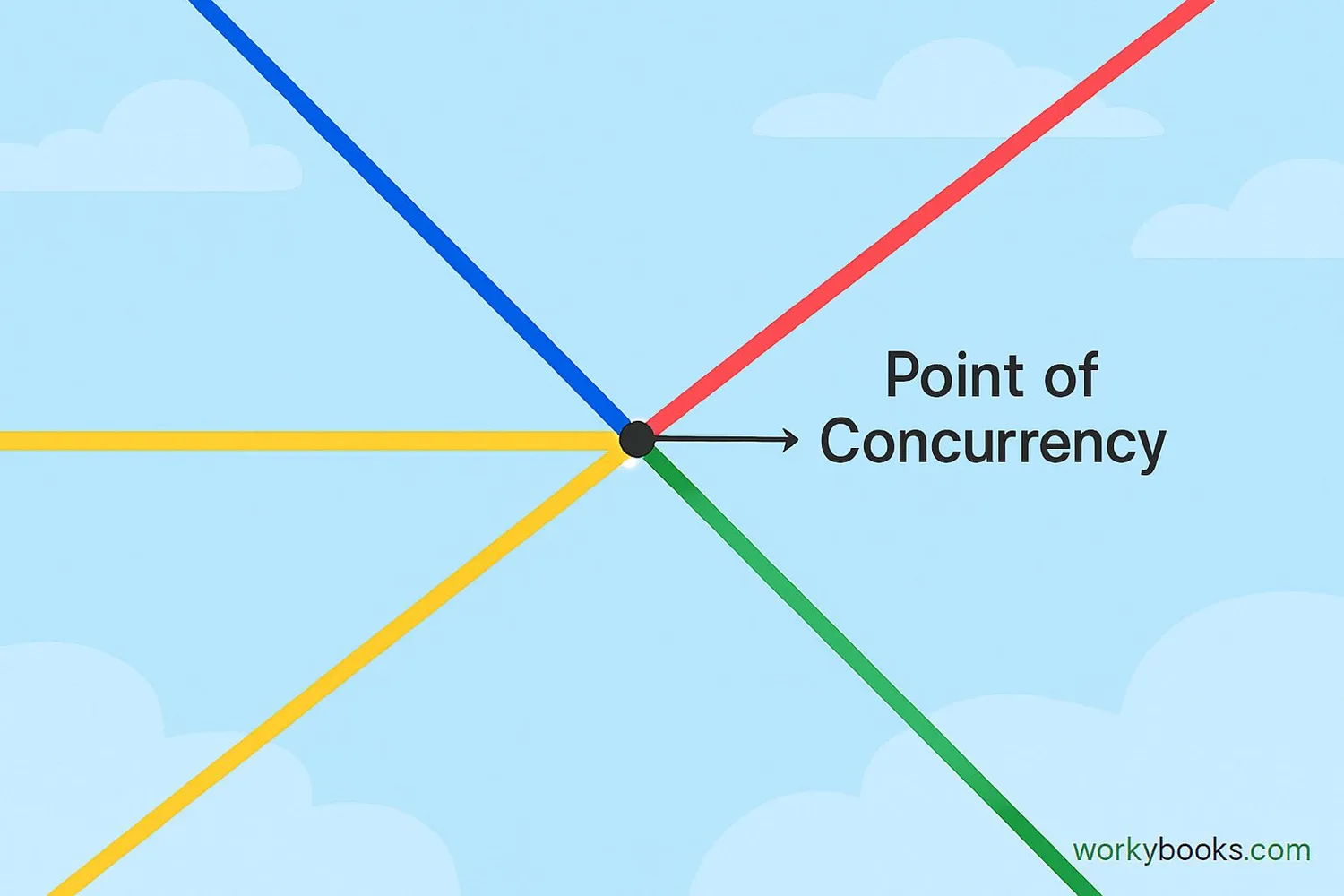
The special point where concurrent lines meet is called the point of concurrency.
This is the exact spot where all the lines cross each other. It's like the center of a star where all the points meet.
Here are some important things to remember about points of concurrency:
- Every set of concurrent lines has exactly one point of concurrency
- The point of concurrency is the solution to the equations of all the lines
- In triangles, different types of concurrent lines have special names for their points of concurrency
Remember
Without a point of concurrency, lines are not concurrent! They must all meet at one common point.
Types of Concurrent Lines in Triangles
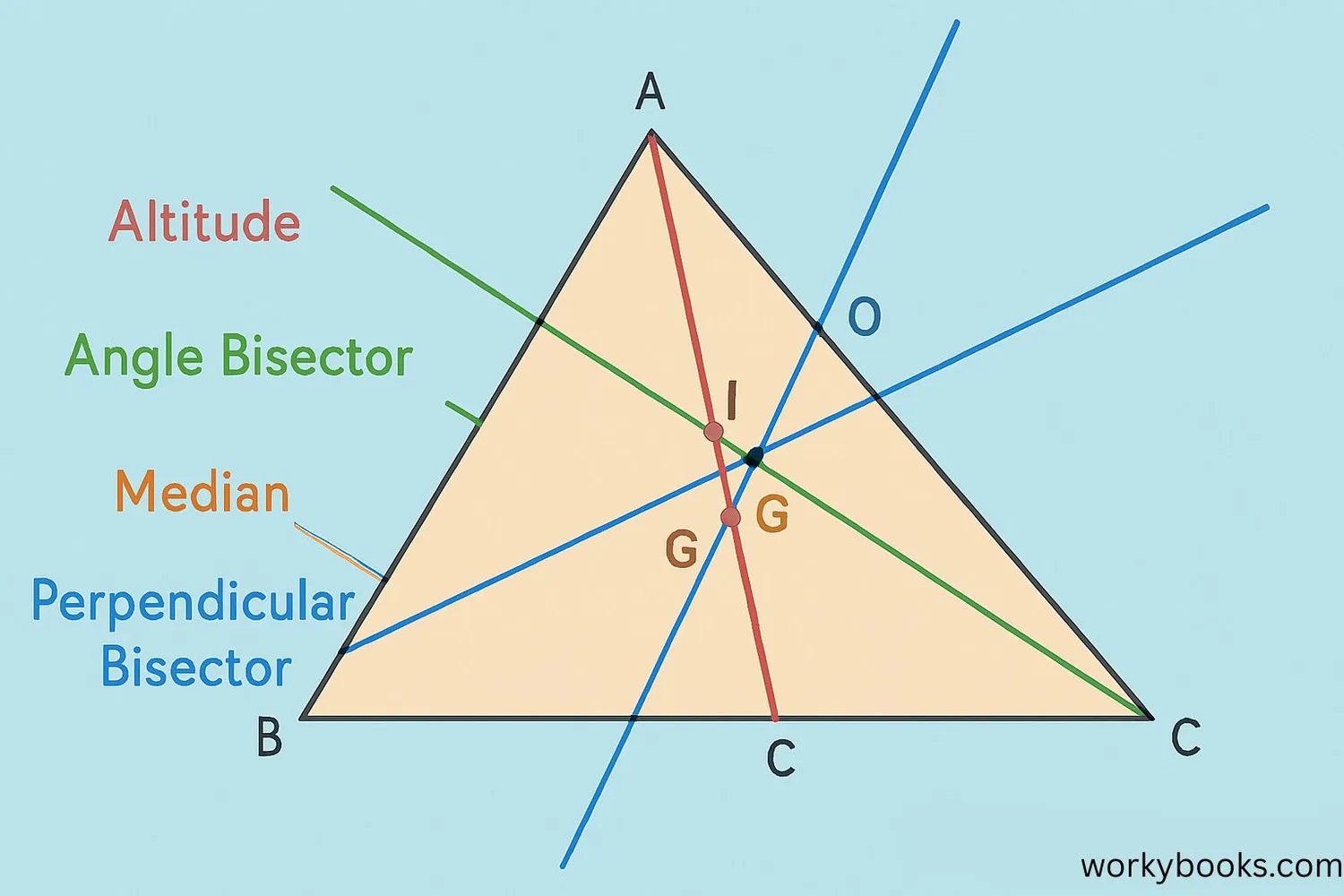
Triangles have special lines that are always concurrent. Each type has its own special name and point of concurrency.
Altitudes
An altitude is a perpendicular line from a vertex to the opposite side. The three altitudes of a triangle meet at the orthocenter.
Angle Bisectors
An angle bisector divides an angle into two equal parts. The three angle bisectors meet at the incenter, which is the center of the incircle.
Medians
A median connects a vertex to the midpoint of the opposite side. The three medians meet at the centroid, which is the triangle's center of gravity.
Perpendicular Bisectors
A perpendicular bisector cuts a side in half at a 90° angle. The three perpendicular bisectors meet at the circumcenter, which is the center of the circumcircle.
Fun Fact
In an equilateral triangle, all four points of concurrency (orthocenter, incenter, centroid, circumcenter) are the same point!
Real-World Examples

Concurrent lines aren't just in math books - they're all around us! Here are some real-world examples:
Example 1: Bicycle Wheel
The spokes of a bicycle wheel all meet at the center hub. This is a perfect example of concurrent lines!
Example 2: Star Shapes
When you draw a star, all the points meet at the center. The lines forming the star are concurrent at the center point.
Example 3: Pyramids
The edges of a pyramid meet at the apex (top point). If you look straight down at a pyramid, the edges appear as concurrent lines.
Example 4: Clock Hands
At 12:00, the hour and minute hands meet at the center of the clock. At that moment, they form concurrent lines.
Next time you're outside, look for examples of concurrent lines in buildings, playground equipment, or even spider webs!
Observation Tip
Look for patterns where multiple straight lines meet at a common point - that's concurrency in action!
Concurrent Lines Quiz
Test your understanding of concurrent lines with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about concurrent lines:
Geometry Trivia
Discover interesting facts about concurrent lines and geometry:
Ancient Discoveries
The concept of concurrent lines was known to ancient Greek mathematicians. Euclid mentioned them in his famous work "Elements" around 300 BCE.
Engineering Applications
Engineers use points of concurrency when designing bridges and buildings to ensure weight is properly distributed and structures are stable.
Space Exploration
NASA scientists use concurrent lines concepts when calculating spacecraft trajectories, where multiple paths converge at a target point.
Mathematical Record
The most concurrent lines possible in a plane is theoretically unlimited! Mathematicians have drawn over 1,000 lines all intersecting at a single point.





