Congruent Figures - Definition, Examples, Quiz, FAQ, Trivia
Learn about congruent shapes and triangles with easy explanations, examples, and practice activities
What are Congruent Figures?
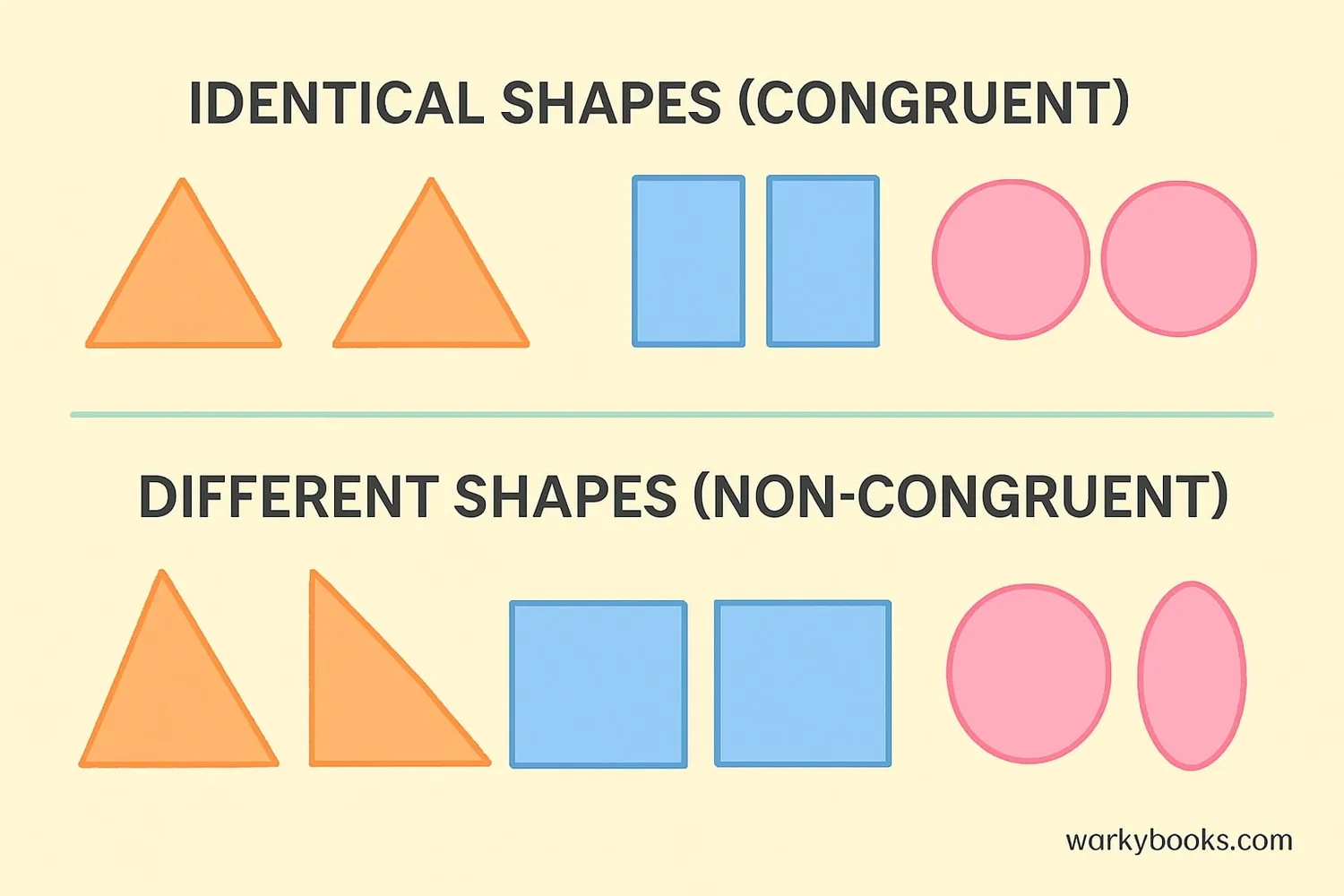
Congruent figures are shapes that have the exact same size and shape. They are identical copies of each other. When you have two congruent figures, you can place one on top of the other and they match perfectly.
The symbol for congruence is ≅. For example, if triangle ABC is congruent to triangle DEF, we write: ΔABC ≅ ΔDEF.
Congruent figures are important in geometry because they help us understand how shapes relate to each other. Architects, engineers, and designers use congruence when creating symmetrical structures and patterns.
Key Concept
Two figures are congruent if all their corresponding sides are equal and all their corresponding angles are equal.
Properties of Congruent Figures
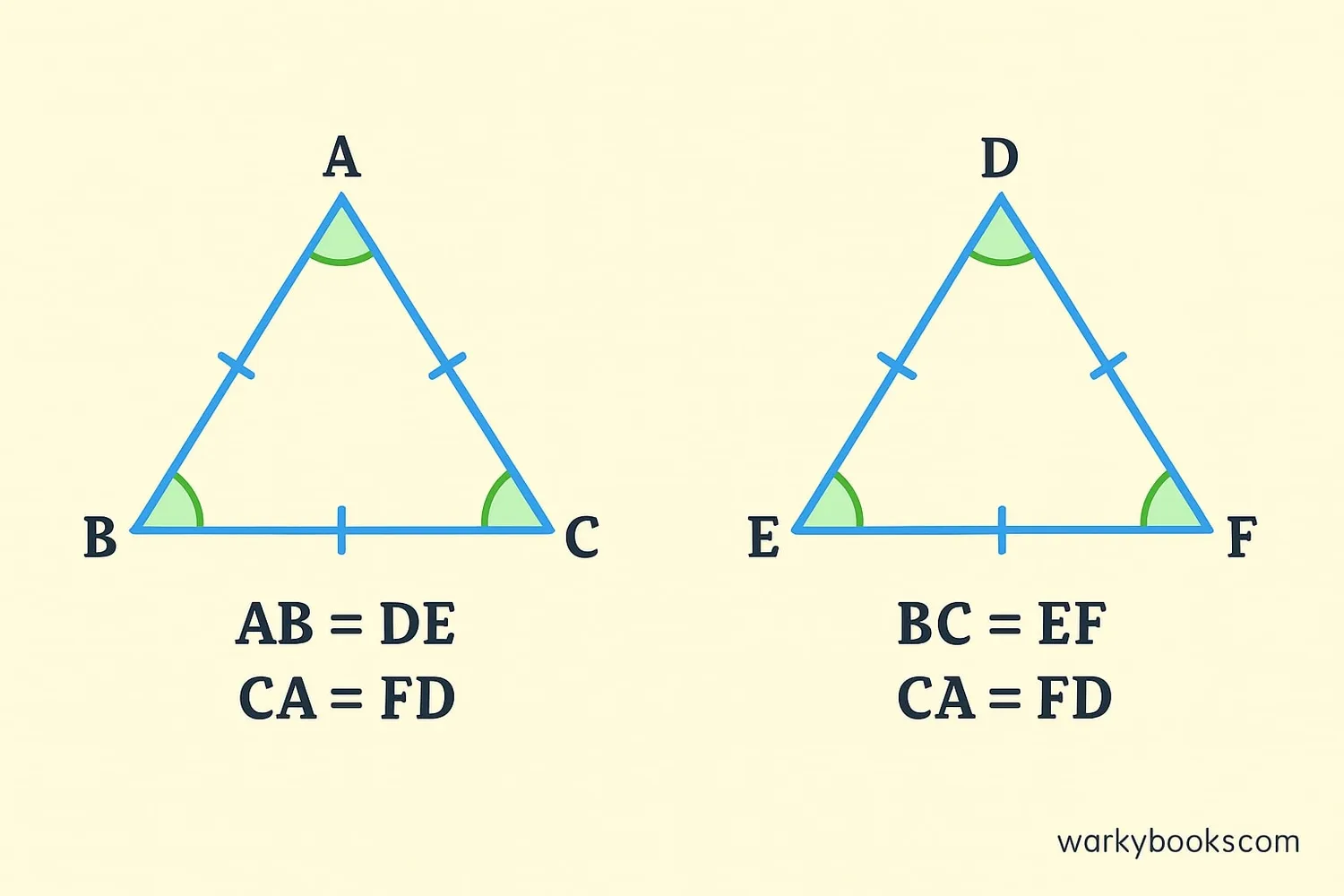
When two figures are congruent, they share these important properties:
1. Corresponding sides are equal: Matching sides have the same length. For example, if AB corresponds to DE, then AB = DE.
2. Corresponding angles are equal: Matching angles have the same measure. If ∠A corresponds to ∠D, then ∠A = ∠D.
3. Same area and perimeter: Since all sides are equal, congruent figures have the same perimeter. They also have the same area because they're the same size and shape.
4. Same shape: Congruent figures are always the same shape. A triangle can't be congruent to a rectangle!
Remember
Congruence is about both size AND shape. Similar figures have the same shape but different sizes.
Transformations and Congruence
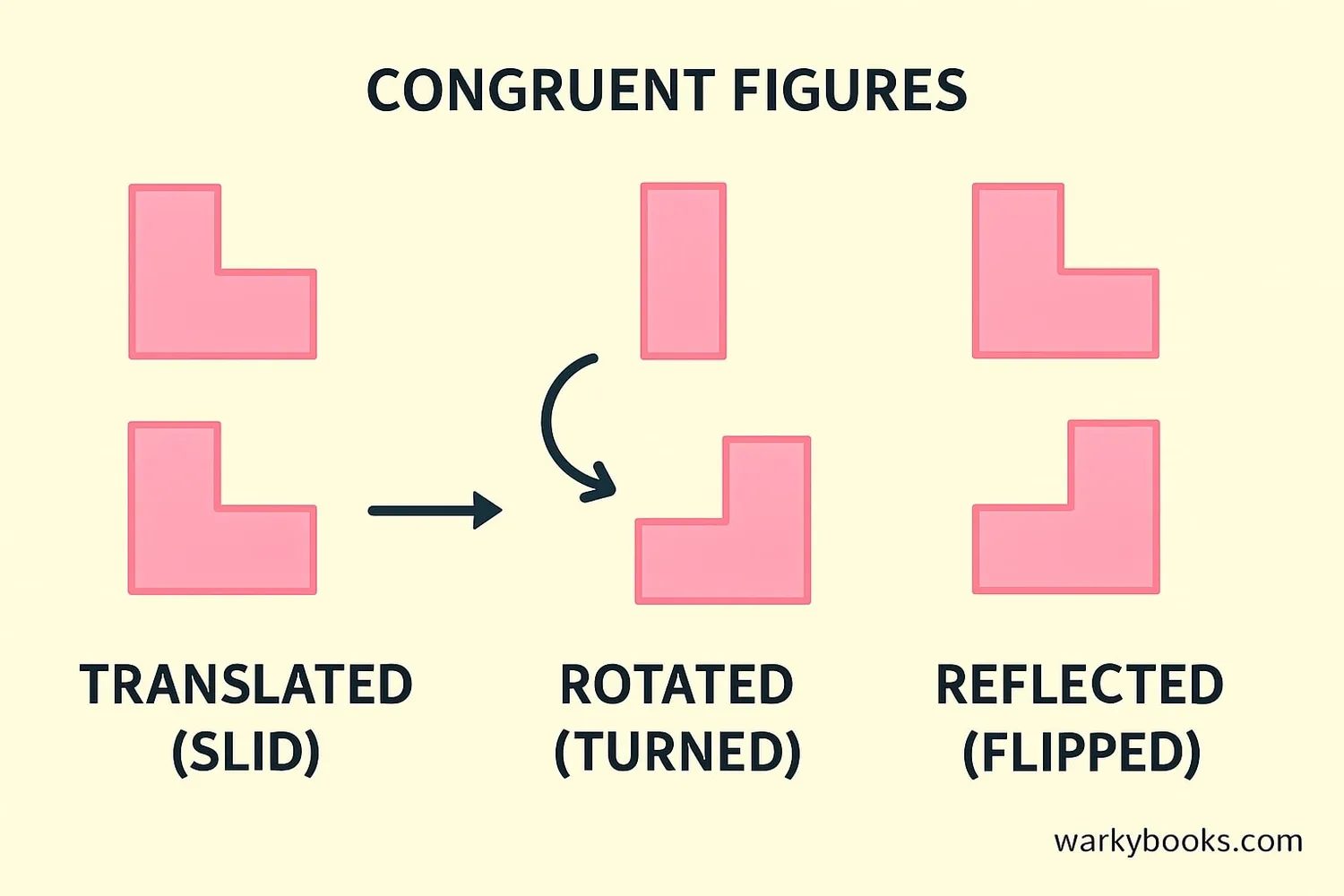
Transformations are movements of shapes that don't change their size or shape. These transformations produce congruent figures:
Translation
Sliding a shape without rotating or flipping it. Also called a "slide".
Rotation
Turning a shape around a fixed point. Also called a "turn".
Reflection
Flipping a shape over a line to create a mirror image. Also called a "flip".
Key Concept
Any combination of translations, rotations, and reflections will produce a figure congruent to the original.
Triangle Congruence Postulates
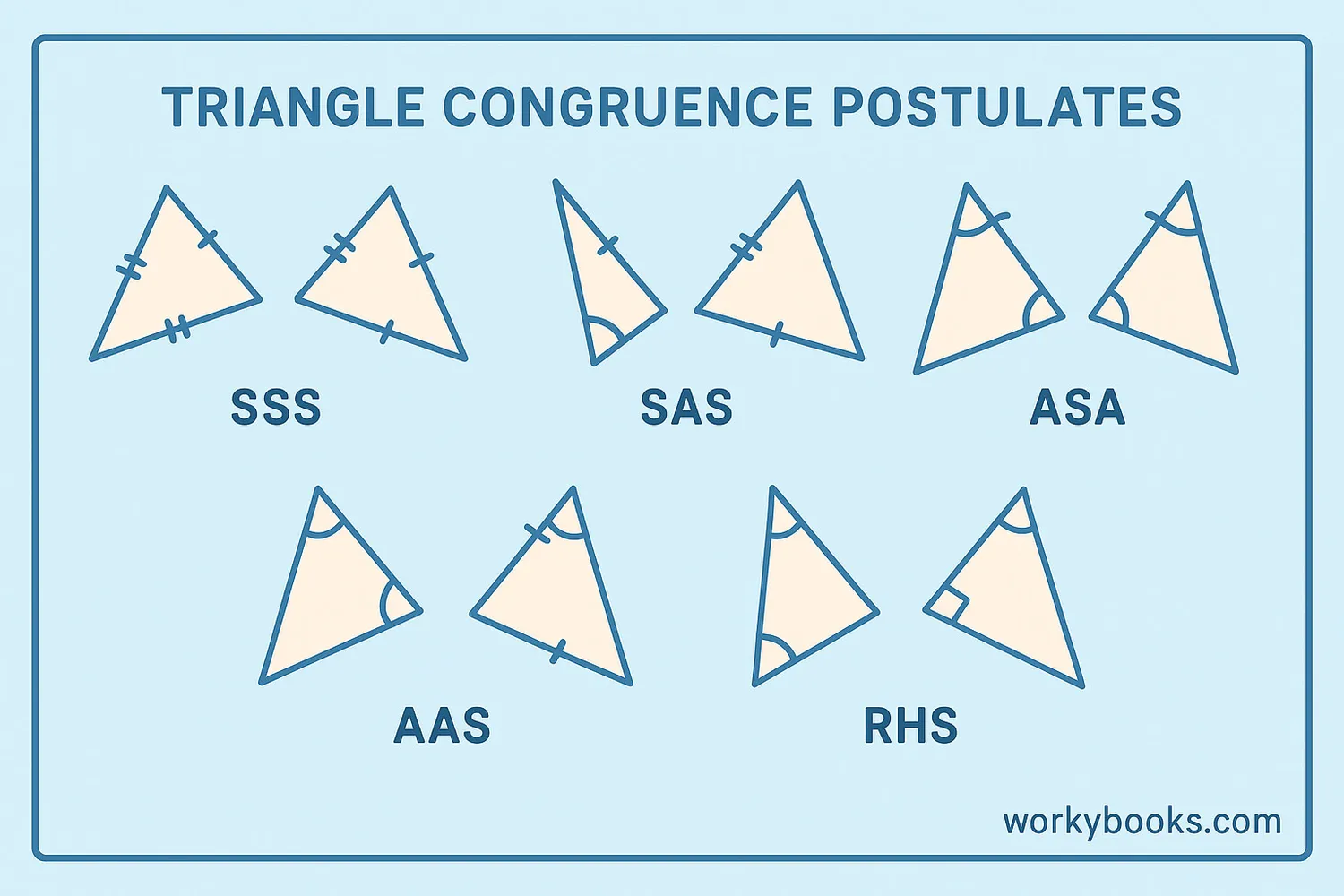
For triangles, we have special rules called congruence postulates that help us prove when two triangles are congruent. Here are the five main postulates:
SSS (Side-Side-Side)
If all three sides of one triangle are equal to all three sides of another triangle, the triangles are congruent.
Example: AB = DE, BC = EF, AC = DF
SAS (Side-Angle-Side)
If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.
Example: AB = DE, ∠B = ∠E, BC = EF
ASA (Angle-Side-Angle)
If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, the triangles are congruent.
Example: ∠A = ∠D, AC = DF, ∠C = ∠F
AAS (Angle-Angle-Side)
If two angles and a non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, the triangles are congruent.
Example: ∠A = ∠D, ∠B = ∠E, BC = EF
RHS (Right angle-Hypotenuse-Side)
If the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one side of another right-angled triangle, the triangles are congruent.
Example: For right triangles: Hypotenuse AC = DF, Side AB = DE
CPCTC (Corresponding Parts)
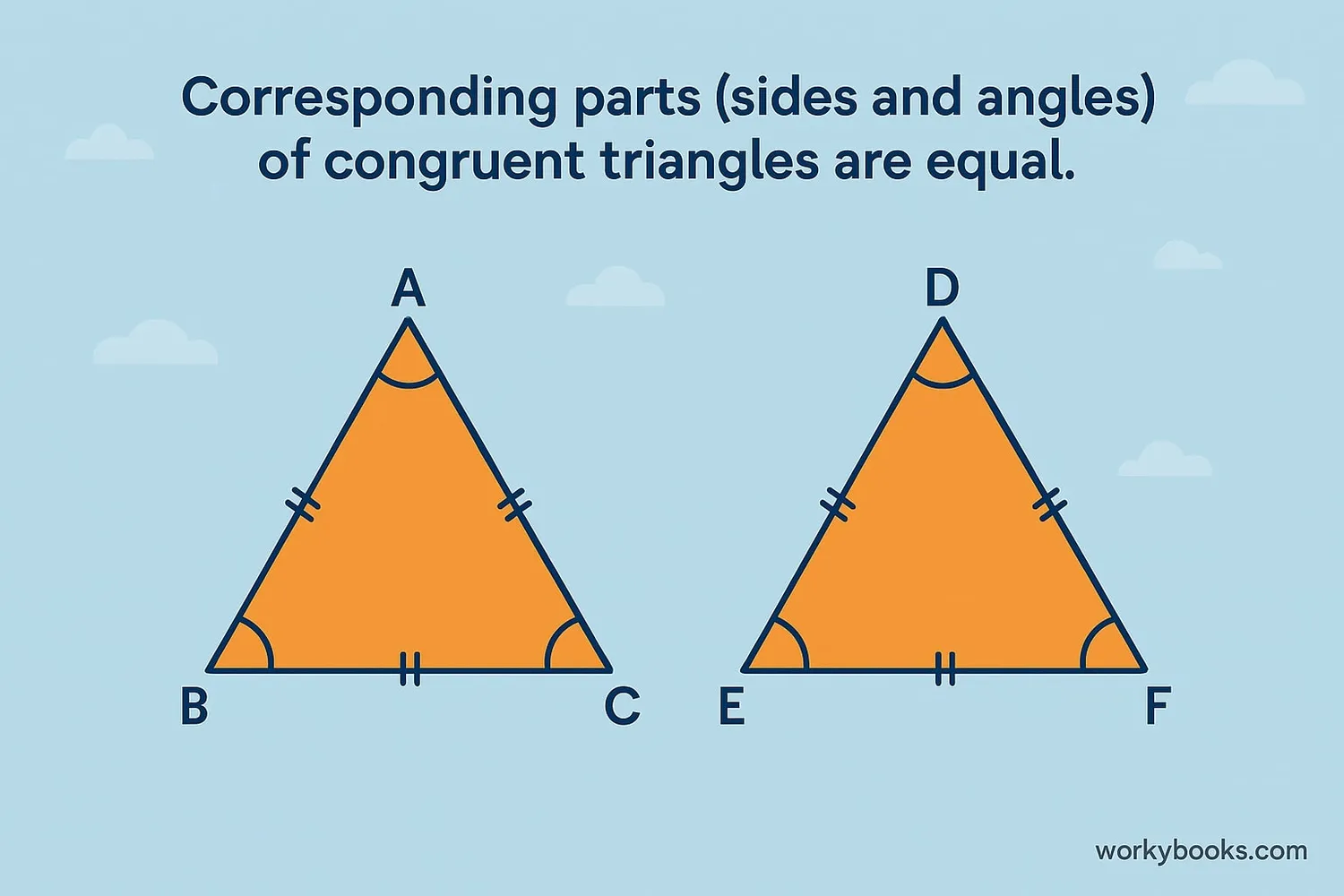
CPCTC stands for "Corresponding Parts of Congruent Triangles are Congruent". This is a very important rule in geometry!
Once we know that two triangles are congruent (using one of the postulates), we can immediately conclude that:
• All corresponding sides are equal
• All corresponding angles are equal
• They have the same area
• They have the same perimeter
CPCTC helps us solve many geometry problems. For example, if we prove two triangles are congruent using SSS, then we know all their angles are equal too, without measuring them!
Remember
CPCTC only works AFTER we've proved triangles are congruent. We can't use it to prove congruence!
Examples and Applications
Example 1: Simple Proof
Given: AB = DE, BC = EF, AC = DF
Conclusion: ΔABC ≅ ΔDEF by SSS postulate
Example 2: Using Transformations
Triangle ABC is rotated 90° around point C. The new triangle is congruent to the original because rotation preserves size and shape.
Example 3: Real-World Application
When architects design symmetrical buildings, they use congruent shapes to create balanced and visually pleasing structures.
Problem Solving Tip
When proving triangles congruent, always look for:
- Shared sides (reflexive property)
- Vertical angles (they're always equal)
- Parallel lines (create equal angles)
Congruent Figures Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about congruent figures:
Geometry Trivia
Discover interesting facts about geometry and congruence:
Ancient Geometry
The concept of congruence dates back to ancient Greek mathematicians like Euclid, who included congruence postulates in his famous work "Elements" around 300 BCE.
Nature's Congruence
Honeybees build honeycombs with congruent hexagonal cells. This efficient shape allows them to store the maximum amount of honey using the least amount of wax.
Space Engineering
NASA engineers use congruence principles when designing spacecraft. Identical components are manufactured to be congruent so they can be replaced during space missions.
Symmetrical Structures
The Taj Mahal in India is famous for its perfect symmetry. Its congruent halves demonstrate how congruence creates visual harmony in architecture.





