Consecutive Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn about number sequences, patterns, and how to work with consecutive numbers
What are Consecutive Numbers?
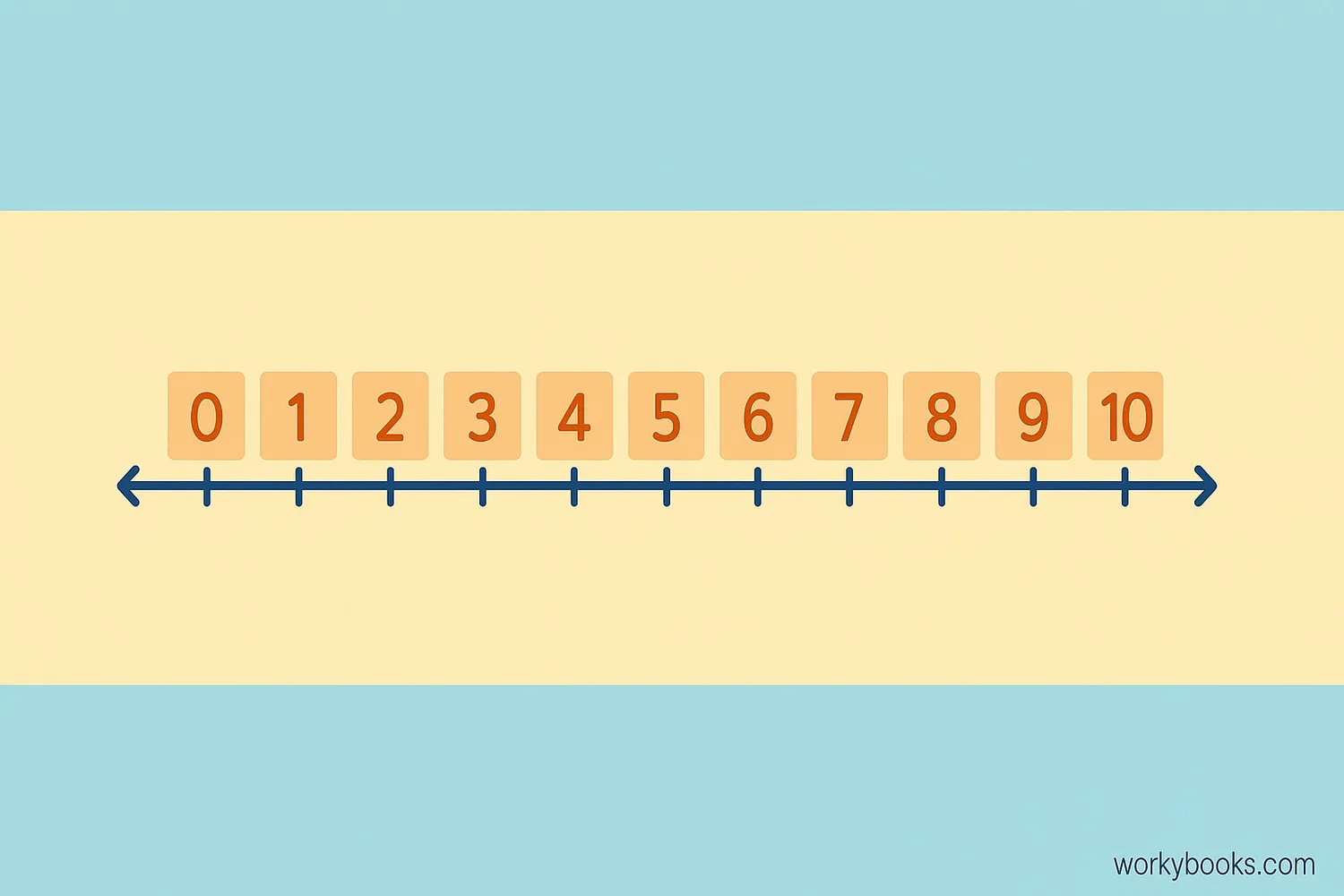
Consecutive numbers are numbers that follow each other in order from smallest to largest, without any gaps. They are like neighbors on the number line.
For example:
These numbers are consecutive because each number is exactly one more than the number before it.
Consecutive numbers are important in math because they help us see patterns, solve problems, and understand how numbers relate to each other.
Key Concept
Consecutive numbers are numbers that come one after another in counting order.
Types of Consecutive Numbers

There are different types of consecutive numbers. Let's look at the main ones:
Consecutive Integers
These are numbers that follow each other in regular counting order:
Consecutive Even Numbers
These are even numbers that follow each other in order:
Consecutive Odd Numbers
These are odd numbers that follow each other in order:
Remember
Consecutive even numbers increase by 2 each time (like 10, 12, 14). Consecutive odd numbers also increase by 2 (like 7, 9, 11).
Patterns and Properties
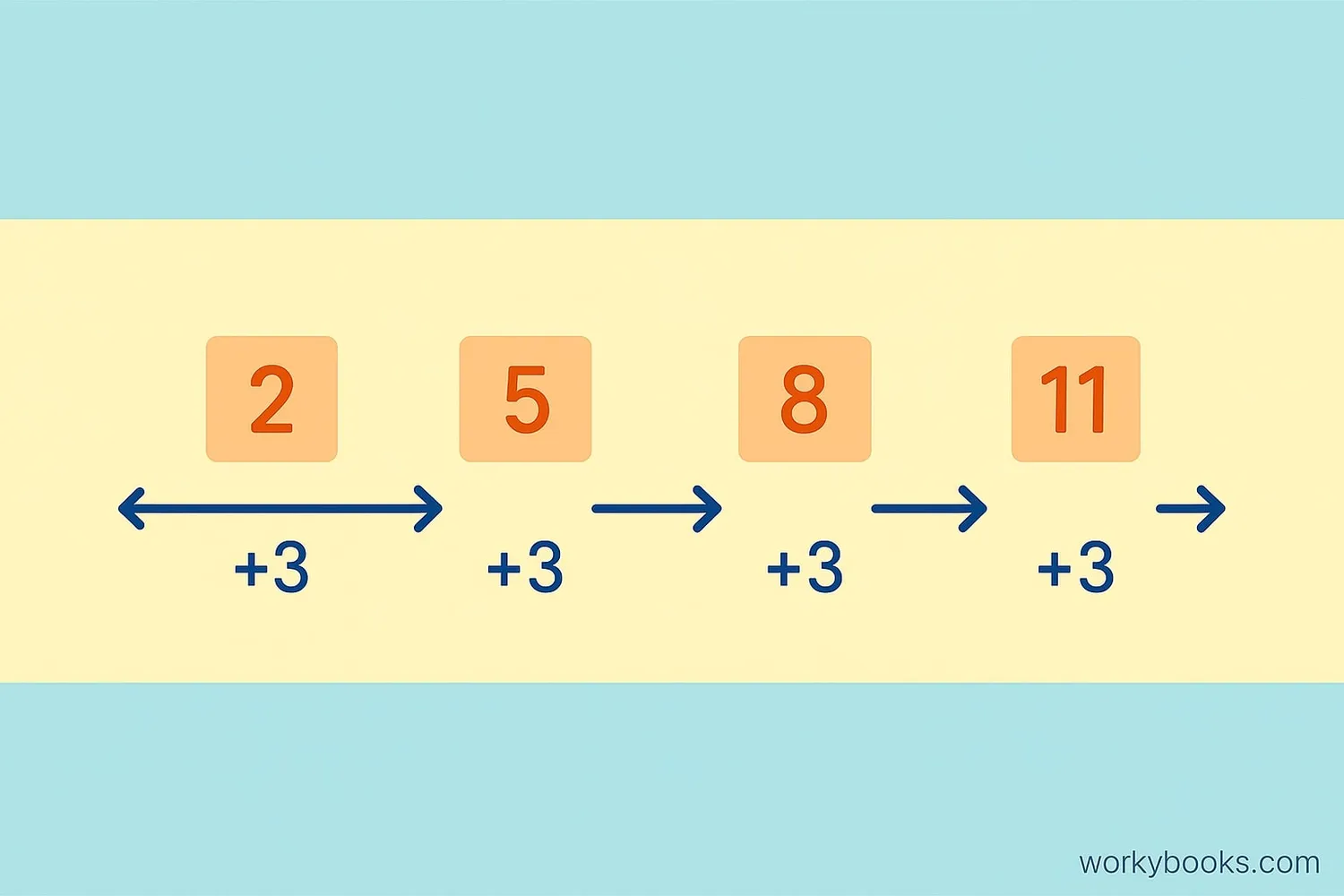
Consecutive numbers have interesting patterns and properties:
Constant Difference: Between any two consecutive numbers, the difference is always 1. For consecutive even or odd numbers, the difference is 2.
Arithmetic Progression: Consecutive numbers form what mathematicians call an arithmetic progression. This means each number is obtained by adding a fixed number (the difference) to the previous number.
Pattern Examples:
- 3, 4, 5 → 4 is exactly in the middle
- 10, 11, 12 → The sum is 33 (10+11+12)
- 7, 8, 9 → The average is 8 (the middle number)
Pattern Tip
For any three consecutive numbers, the middle number is always the average of the three numbers.
Sum of Consecutive Numbers

Adding consecutive numbers can be done quickly with a special formula:
Sum Formula
Where n is the count of numbers
Example: Find the sum of 1 + 2 + 3 + 4 + 5
First number = 1
Last number = 5
Count of numbers (n) = 5
Sum = (1 + 5) × 5 ÷ 2 = 6 × 5 ÷ 2 = 30 ÷ 2 = 15
This formula works for any set of consecutive numbers!
Remember
The sum of consecutive numbers starting from 1 is called a triangular number.
Algebra with Consecutive Numbers
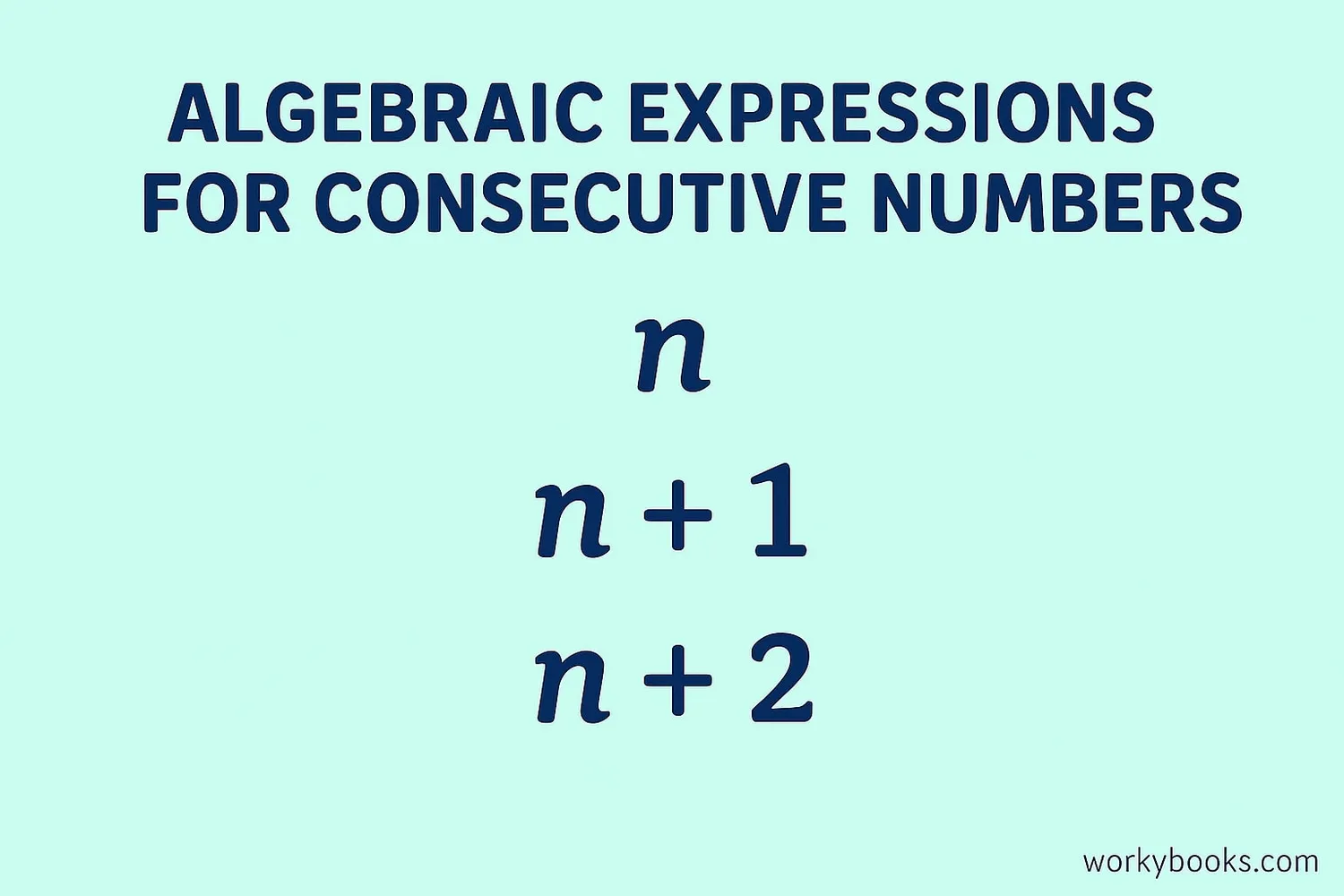
In algebra, we use variables to represent consecutive numbers. This helps us solve problems with unknown numbers.
Representing Consecutive Numbers:
- Three consecutive numbers: n, n+1, n+2
- Three consecutive even numbers: n, n+2, n+4
- Three consecutive odd numbers: n, n+2, n+4
Let the first number be n
Then the next numbers are n+1 and n+2
Their sum: n + (n+1) + (n+2) = 24
3n + 3 = 24
3n = 21
n = 7
So the numbers are 7, 8, and 9
Algebra Tip
When working with consecutive even or odd numbers, remember they increase by 2 each time.
Consecutive Numbers Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about consecutive numbers:
Number Trivia
Discover interesting facts about numbers:
Ancient Number Systems
The concept of consecutive numbers has been around for thousands of years. Ancient Egyptians used consecutive numbers in their construction projects, including building the pyramids!
Gauss and Consecutive Numbers
The famous mathematician Carl Friedrich Gauss discovered the formula for the sum of consecutive numbers when he was just 8 years old! His teacher had asked the class to add all numbers from 1 to 100.
Numbers in Nature
Consecutive numbers appear in nature! The number of petals on flowers often follow consecutive patterns like 3, 5, 8, 13 - which are part of the Fibonacci sequence.
Largest Prime Number
The largest known prime number has over 24 million digits! While it's not consecutive with other numbers, finding prime numbers involves understanding number patterns.





