Constructing an Angle Bisector - Definition, Examples, Quiz, FAQ, Trivia
Learn to divide angles into two equal parts with step-by-step instructions and practice activities
What is an Angle Bisector?
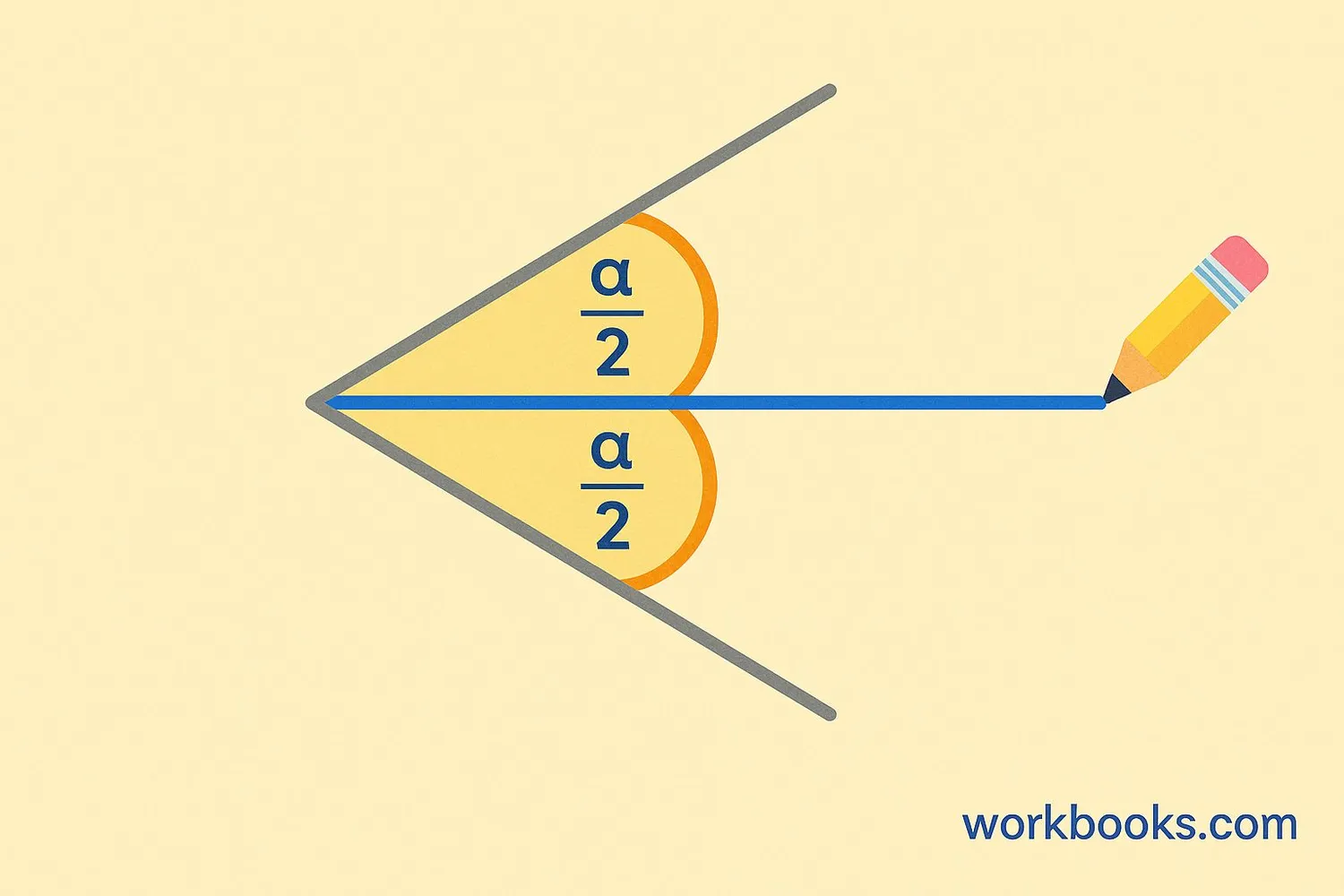
An angle bisector is a line or ray that divides an angle into two equal angles.
Think of it like cutting a slice of pizza exactly in half so both pieces are the same size. In geometry, we use special tools like a compass and straightedge to create perfect angle bisectors.
Angle bisectors are important in geometry because they help us solve problems, create symmetrical shapes, and find the center of angles. You'll use this skill in many math classes as you advance!
Key Concept
The angle bisector divides an angle into two congruent angles (angles with the same measure).
How to Construct an Angle Bisector
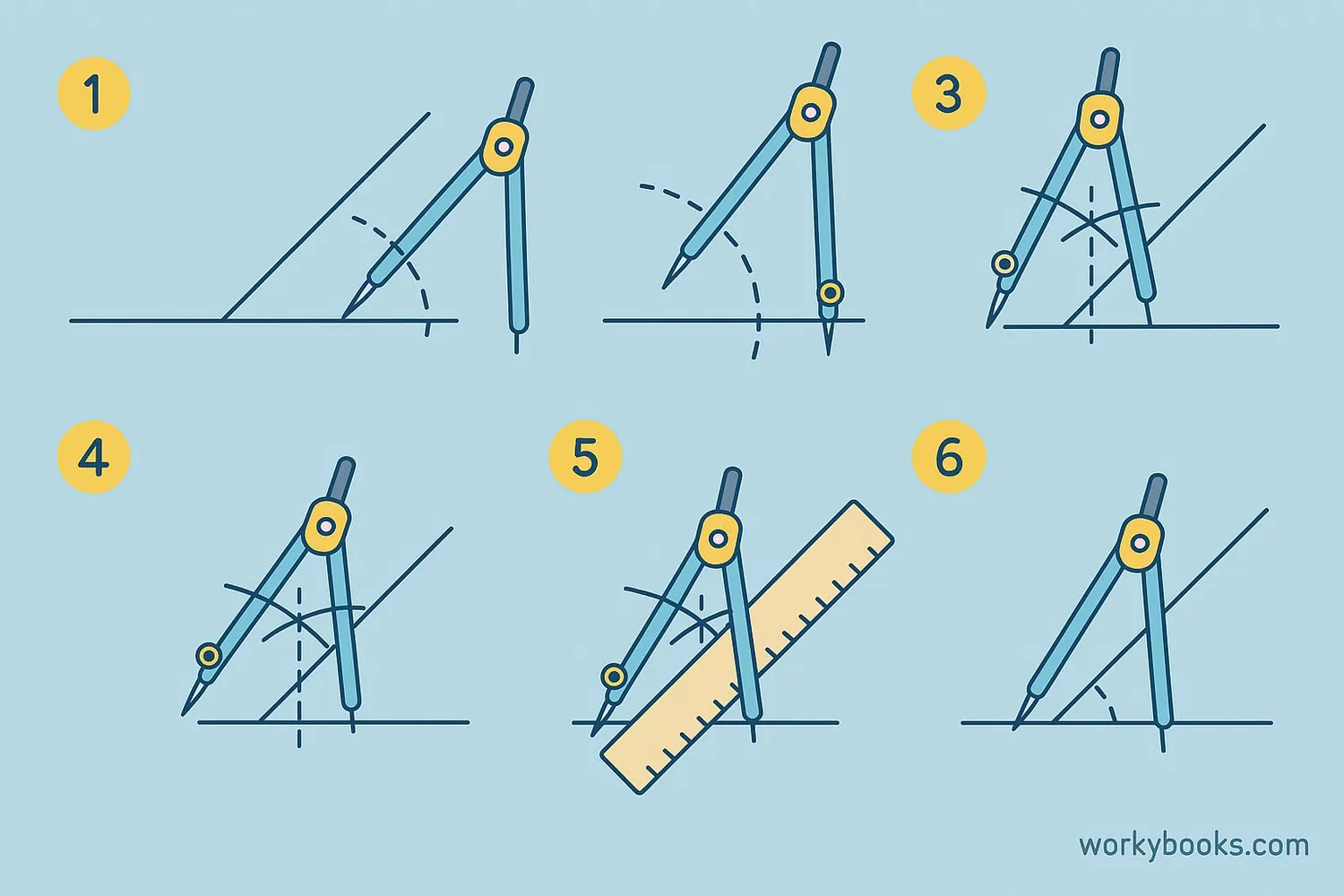
Follow these steps to construct an angle bisector using a compass and straightedge:
Remember
Always keep your compass at the same width after drawing the first arc. This ensures your bisector will be accurate.
The Angle Bisector Theorem
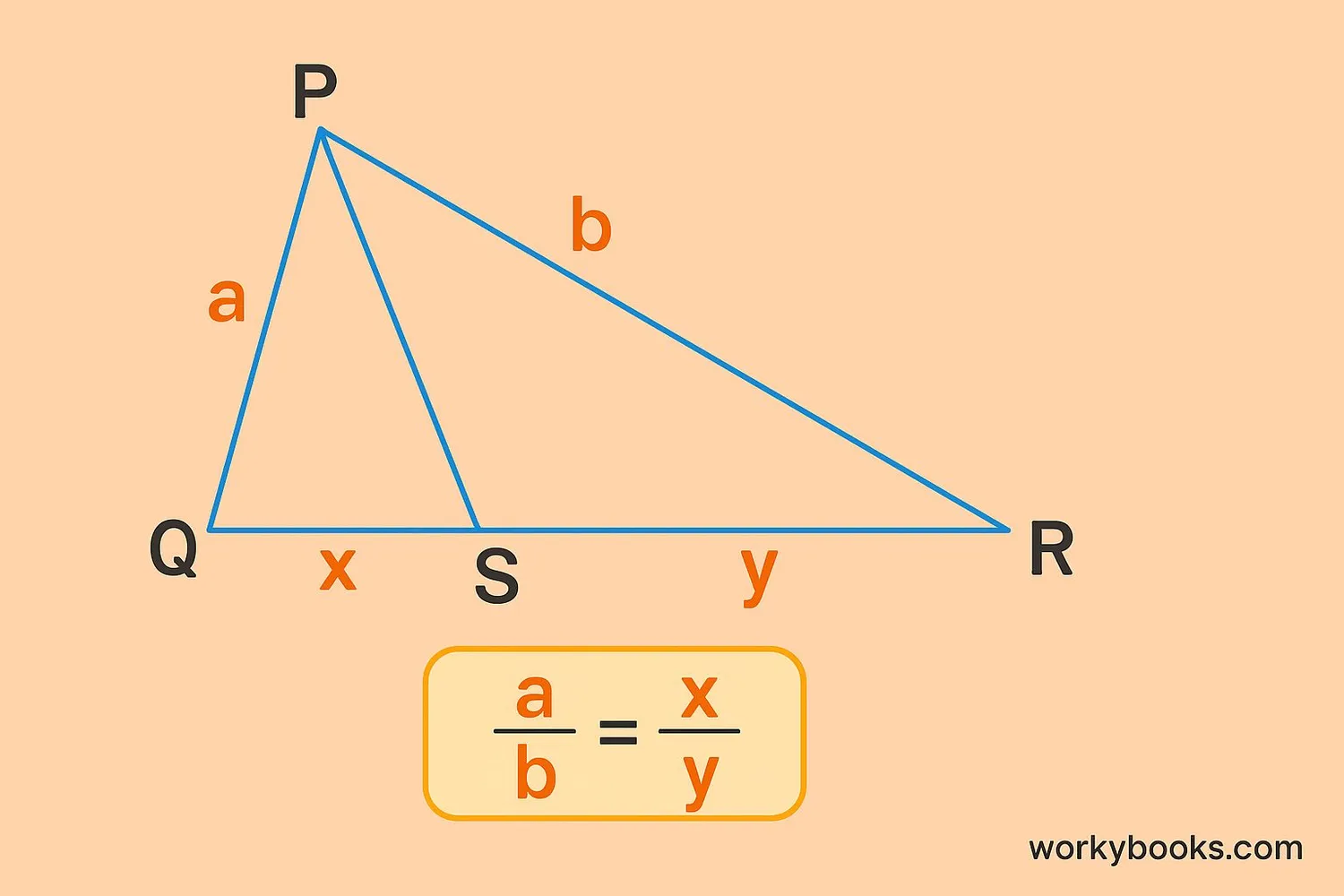
The Angle Bisector Theorem is an important rule that helps us understand how bisectors work in triangles:
Angle Bisector Theorem
If a ray bisects an angle of a triangle, it divides the opposite side into segments proportional to the adjacent sides.
This theorem helps us solve for unknown lengths in triangles when we know an angle has been bisected.
Examples and Practice
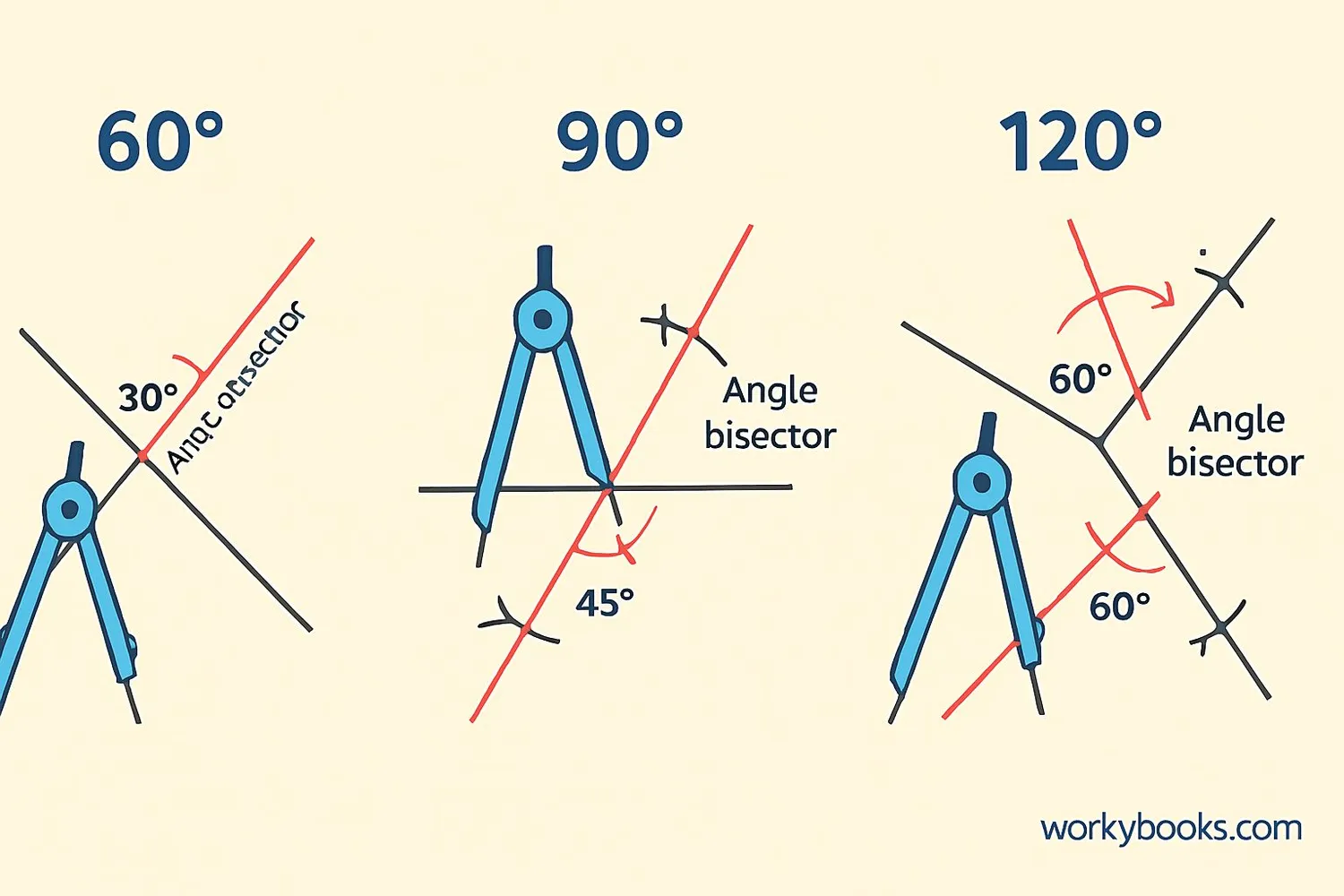
Let's practice constructing angle bisectors with different types of angles:
Example 1: Constructing a 60° Angle Bisector
1. Draw a 60° angle using a protractor or by constructing an equilateral triangle
2. Follow the standard steps to bisect the angle
3. Verify with a protractor that you now have two 30° angles
Example 2: Bisecting a Right Angle
1. Draw a 90° angle (a right angle)
2. Construct the bisector
3. Verify that you have two 45° angles
Example 3: Real-World Application
Angle bisectors are used in architecture to create symmetrical designs and in navigation to find equidistant points. They also help in sports like billiards to calculate bank shots!
Practice Tip
Try drawing angles of different measures and bisecting them. Always verify with a protractor to check your accuracy.
Angle Bisector Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about angle bisectors:
Geometry Trivia
Discover interesting facts about angles and geometry:
Ancient Geometry
The ancient Egyptians were using geometric principles for land surveying as early as 3000 BC. They developed techniques to divide land using angles and bisectors after Nile River floods.
Nature's Angles
Honeybees use angle bisectors when building honeycombs! They create perfect hexagons by bisecting 120° angles to form the hexagonal pattern that makes their hives efficient and strong.
Space Navigation
NASA engineers use angle bisectors in spacecraft navigation. When calculating trajectories to other planets, they use angle bisectors to determine optimal paths that conserve fuel.
Geometric Records
The largest human-made angle bisector was created in 2018 in Dubai. Engineers used laser technology to bisect a 150° angle across a 500-meter distance for a construction project.





